一种无人艇路径跟踪控制器的设计与验证

文元桥， 杨 吉， 周 阳， 高欣国， 肖长诗

(1.武汉理工大学 航运学院， 武汉 430063； 2.内河航运技术湖北省重点实验室， 武汉 430063;3.国家水运安全工程技术研究中心， 武汉 430063)

无人艇(Unmanned Surface Vessel，USV)作为一种能自主航行和智能作业的无人驾驶小型船舶，随着传感器技术的进步和现代控制理论的发展，逐步从仿真模拟研究转入桥梁检测[1]、海洋测绘[2]、水质监测[3]和水上搜救[4]等工程应用研究中。

无人艇路径跟踪控制是开展无人艇编队控制和协同控制等研究的基础。路径跟踪控制器一般具有2种结构：

1) 将控制器分为外环制导和内环控制2个环节。

2) 将制导和控制集成在一起，这种结构的控制器通常基于神经网络[5-6]等方法实现。

当前路径跟踪控制器大多采用内外环分离的结构。无人艇路径跟踪控制器的内环控制方法主要有滑模控制[7]、双极模糊控制[8]、反步法[9]和动态面控制[10]等，这些算法大多对数学模型的精度和传感器的性能要求较高，导致在工程上较难实现。无人艇路径跟踪控制器的外环制导律主要是常规的Line-Of-Sight (LOS)制导算法[11]和针对外界环境干扰的Integral Line-Of-Sight(ILOS)制导算法[12]，这2种算法只适于对直线参考路径进行跟踪[13]。实际应用中的无人艇因航行和作业任务的需要，应兼具对直线路径和曲线路径进行跟踪的能力。

本文以武汉理工大学iNav-II型USV(见图1)为研究对象，对其在实际应用中遇到的路径跟踪控制问题进行研究。首先，在利用带遗忘因子的递推最小二乘法对无人艇的状态空间型船舶线性数学模型进行在线参数辨识的基础上，实现对USV操纵响应模型参数的在线估算。其次，基于内模控制和L1制导算法设计并实现无人艇的路径跟踪控制器。最后，通过一系列实船试验验证路径跟踪控制器的性能。

1 iNav-II型USV

iNav-II型USV是纯电动的玻璃钢制无人艇，设计总长3.96 m，型宽1.55 m，吃水0.3～0.5 m。该USV的推进器是一台吊舱推进器，其偏转角度限制为-25°～25°。iNav-II型无人艇配置有毫米波雷达、风速风向仪、惯性测量与导航系统、差分全球定位系统(Differential Global Positioning System, DGPS)和船岸无线通信系统。

2 USV运动数学模型和参数估计

图2为iNav-II型USV平面运动示意，其中：Ψ为USV的艏向角；δr为吊舱推进器的偏转角度。USV的状态空间型船舶线性数学模型可表示为

(1)

根据USV上DGPS输出的经纬度坐标数据可计算出USV在大地坐标系下正东方向和正北方向上的速度分量Ev和Nv。[14]结合陀螺罗经输出的艏向角Ψ，可通过式(2)计算得到在USV附体坐标系下船体bx轴上的速度u和by轴上的速度v。艏摇角速度r由USV上安装的高精度惯性测量单元(IMU)测量得到。

(2)

将得到的USV运动状态参数代入到式(1)中，并在递推最小二乘法[15]的基础上引入值为0.98的遗忘因子，可实现对USV的状态空间型船舶线性数学模型参数的在线辨识。

将式(1)解耦艏摇和横移运动并忽略横移项的影响，经过拉式变换可得一阶线性Nomoto模型为

(3)

在USV做定常运动、舵角较小的情况下，该模型可近似描述USV的操纵响应特性。采用该模型可大大简化角速度控制器的设计。式(3)中USV的操纵性指数K和T可在对式(1)进行在线参数辨识的基础上通过式(4)计算得到。[16]

(4)

3 USV路径跟踪控制器设计

3.1 路径跟踪控制器结构

图3为路径跟踪控制器结构。USV路径跟踪控制器采用制导环节与控制环节分离的结构，由内环基于内模控制的USV艏摇角速度控制器和外环L1制导律2部分组成。L1制导律根据参考路径信息和USV的运动状态数据输出无人艇跟踪参考路径所需的参考艏摇角速度指令rcmd。制导环节输出的参考艏摇角速度指令作为输入信号进入控制环节中，而控制环节输出的吊舱推进器偏转角度指令δr-cmd将由吊舱推进器的转向结构予以执行。

3.2 基于内模控制的USV艏摇角速度控制器

内模控制(Internal Model Control, IMC)是在Smith预估控制的基础上发展起来的，具有控制结构简单、对模型误差具有较强的鲁棒性、调节参数少和调参方向明确等特点。[17]

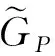
(5)

(6)

(7)

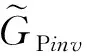
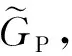
(8)

为便于在实船试验中实现式(8)，进一步将式(8)改写为经典的PID控制结构，则式(8)可等效为一个PI控制器，即

(9)

(10)

(11)

由式(9)可知，基于内模控制的USV艏摇角速度控制器中含有USV操纵性指数K、T和增益参数β等3个参数。控制器中的USV操纵性指数K和T由上述在线参数估计得到。因此，基于内模控制的USV艏摇角速度控制器在实际应用中还需通过现场调试来确定影响控制器响应速度和鲁棒性的增益参数β。

3.3 L1制导律

PARK等[19]在短程战术导弹末端制导律中的比例导引法的基础上提出L1制导算法，并通过理论分析和开展基于L1制导算法的固定翼无人机飞行试验来证明L1制导算法的稳定性。L1制导算法既适用于直线路径制导，也适用于曲线路径制导，且其因在曲线路径制导方面较好的性能表现而被较多固定翼无人机所采用。因此，采用L1制导算法作为iNav-II型USV路径跟踪的制导律。

L1制导算法见图6，其中：u为艏向速度；L1为USV到参考点的直线距离；η为艏向与USV和参考点连线的夹角。L1为定值，结合当前船位和参考路径信息可确定参考路径上参考点的坐标。将USV回到参考路径的运动过程近似看成圆周运动，由式(12)可计算出USV从当前船位跟踪参考路径所需的横向加速度指令acmd。结合式(13)，可根据横向加速度acmd进一步求得USV进行路径跟踪所需的参考艏摇角速度rcmd，从而实现USV路径跟踪过程中的制导环节。

(12)

L1=2Rsinη

(13)

4 实船试验

在武汉市东湖水域进行实船试验，试验水域开阔且无遮挡，试验船速为2.0 m/s，试验场景见图7。实船试验中内模控制的增益参数β设为4.25，L1制导律中的L1设为15 m。试验过程中在线估计出来的iNav-II型USV的操纵性指数K约为0.75，T约为1.2。

为验证所设计的基于内模控制的USV艏摇角速度控制器的实际控制效果，分别进行参考艏摇角速度为5 (°)/s和-12 (°)/s的USV艏摇角速度控制试验。艏摇角速度控制试验结果分别见图8和图9，试验结果表明，基于内模控制结构的USV艏摇角速度控制器能有效控制USV的艏摇角速度，且在艏摇角速度保持阶段的误差较小。

进行直线路径跟踪试验(见图10)。直线路径跟踪试验的参考路径约长410 m。直线路径跟踪的航迹误差见图11，试验结果表明所设计的路径跟踪控制器能较好地实现iNav-II型USV对直线路径的跟踪，且航迹误差控制在±1 m以内。

USV实际航行过程中因避碰或作业任务的需求，需具有跟踪连续曲线路径进行机动航行的能力。因此，设计一组参考路径由4个半径为80 m的圆弧组成的连续曲线路径跟踪试验(见图12)。试验结果表明，所设计的路径跟踪控制器能实现iNav-II型USV对连续曲线路径的跟踪，且航迹误差可控制在±5 m以内。

图14为圆形路径跟踪的轨迹，假设iNav-II型USV执行对图中所示的气胀式救生筏的警戒护航任务，警戒区域是以救生筏为圆心的半径50 m的圆形区域，USV对这一圆形参考路径进行路径跟踪。圆形参考路径跟踪结果表明，USV进行圆形路径跟踪的航迹误差在±5 m以内，能实现无人艇对救生筏的警戒护航(见图15)。

USV在实际执行任务时的参考路径通常由路径规划算法运算生成，且参考路径多由直径路径和曲线路径混合组成。因此，设计一组基于Dubins路径[20]的复杂路径跟踪试验(见图16)。参考路径包含9段直线路径和11段曲线路径，总长约2 370 m。

复杂路径跟踪试验结果表明，iNav-II型USV跟踪复杂路径的航迹误差在±7 m以内，在直线路径和曲线路径衔接处的航迹误差较大(见图17)。

5 结束语

针对iNav-II型USV的路径跟踪问题，设计并实现一种基于内模控制和L1制导算法的USV路径跟踪控制器。通过系统辨识的方法确定基于内模控制的USV艏摇角速度控制器中USV操纵性指数的值。在开阔水域的实船试验证明结合内模控制和L1制导算法的路径跟踪控制器能较好地实现iNav-II型USV对直线路径和曲线路径的跟踪。考虑到本文采用的一阶线性操纵响应模型不能较好地适用于USV机动航行、舵角比较大的情况，下一步将研究采用非线性模型来设计USV控制器，以提高控制器的适应能力和精度。

[1] ELLENRIEDER K D V. Development of a USV-Based Bridge Inspection System[C]//Oceans. IEEE, 2016:1-10.

[2] IDRIS M H B M, SAHALAN M I, ABIDIN Z B Z, et al. Design and Development of an Autonomous Surface Vessel for Inland Water Depth Monitoring[C]//International Conference on Computer and Communication Engineering. IEEE, 2017:177-182.

[3] SIYANG S, KERDCHAROEN T. Development of Unmanned Surface Vehicle for Smart Water Quality Inspector[C]//International Conference on Electrical Engineering/ electronics, Computer, Telecommunications and Information Technology. IEEE, 2016:1-5.

[4] MATOS A, MARTINS A, DIAS A, et al. Multiple Robot Operations for Maritime Search and Rescue in EuRathlon 2015 Competition[C]//Oceans. IEEE, 2016:1-7.

[5] 董早鹏, 刘涛, 万磊,等. 基于Takagi-Sugeno模糊神经网络的欠驱动无人艇直线航迹跟踪控制[J]. 仪器仪表学报, 2015, 36(4):863-870.

[6] MU D D, WANG G F, FAN Y S. Design of Adaptive Neural Tracking Controller for Pod Propulsion Unmanned Vessel Subject to Unknown Dynamics[J]. Journal of Electrical Engineering & Technology, 2017, 12(6):2365-2377.

[7] SONNENBURG C R, Woolsey C A. Modeling, Identification, and Control of an Unmanned Surface Vehicle[J]. Journal of Field Robotics, 2013, 30(3):371-398.

[8] 燕聃聃, 文元桥, 肖长诗,等. 吊舱推进的小型水面无人船航迹控制系统设计[J]. 船海工程, 2017, 46(4):210-214.

[9] FAN Y, SUN Y, WANG G. On Model Parameter Identification and Trajectory Tracking Control for USV Based on Backstepping[C]//Control Conference, 2017 36th Chinese. IEEE, 2017:4757-4761.

[10] SHIN J, DONG J K, LEE Y I. Adaptive Path-Following Control for an Unmanned Surface Vessel Using an Identified Dynamic Model[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(3):1143-1153.

[11] FOSSEN T I, BREIVIK M, SKJETNE R. Line-Of-Sight Path Following of Underactuated Marine Craft[J]. IFAC Proceedings Volumes, 2003, 36(21): 211-216.

[12] CAHARIJA W, PETTERSEN K Y, BIBULI M, et al. Integral Line-Of-Sight Guidance and Control of Underactuated Marine Vehicles: Theory, Simulations and Experiments[J]. IEEE Transpactions on Control Systems Technology, 2014:147-148.

[13] 张国庆. 超恶劣海况下船舶运动简捷鲁棒自适应控制[D].大连:大连海事大学,2015.

[14] KARNEY C F F. Algorithms for Geodesics[J]. Journal of Geodesy, 2013, 87(1):43-55.

[15] ZHU M, HAHN A, WEN Y, et al. Parameter Identification of Ship Maneuvering Models Using Recursive Least Square Method Based on Support Vector Machines[J]. International Journal on Marine Navigation and Safety of Sea Transportation, 2017, 11(1):23-29.

[16] 张显库. 船舶运动简捷鲁棒控制[M]. 北京：科学出版社, 2012:17-23.

[17] 郑恩让, 阮士涛, 王黎. 基于失配模型的内模控制器的设计[J]. 控制工程, 2016, 23(4x):532-537.

[18] SAARI H, DJEMAI M. Ship Motion Control Using Multi-Controller Structure[J]. Ocean Engineering, 2012, 55(4):184-190.

[19] PARK S, DEYST J, HOW J. A New Nonlinear Guidance Logic for Trajectory Tracking[C]//Proceedings of the AIAA Guidance. Navigation and Control Conference, 2004:2004-4900.

[20] 刘乐柱, 肖长诗, 文元桥. 基于Dubins路径的无人艇运动规划算法[J]. 计算机应用, 2017, 37(7):2114-2117.