基于LINGO模型的VTS雷达站选址-配置

孙耀华， 戴 冉， 张超越， 刘高磊， 赵延鹏， 张 锋

(大连海事大学 航海学院，辽宁 大连 116026)

船舶交通管理(Vessel Traffic Services，VTS)系统的主要功能是搜集和处理船舶交通信息，从而对水域内的船舶实施监控和组织管理。[1]作为VTS系统的重要组成部分，VTS雷达站的选址和雷达设备的配置在很大程度上影响着VTS系统功能的发挥。研究VTS雷达站选址和配置问题，需综合考虑雷达站的建设成本、雷达的探测性能和最终的覆盖效果等因素，最后在成本尽可能小的情况下达到覆盖效果最优的目标。

目前对雷达站选址-配置问题的研究比较少。TOREGAS等[2]提出集合覆盖思想，在满足覆盖要求的条件下使建站数量最少；CHURCH等[3]提出最大覆盖的思想，在服务站数量已知的前提下，达到最大覆盖的效果；史云剑[4]研究雷达站的盲区问题，并给出雷达最大作用距离和最小作用距离的计算方法，但没有提出选址的具体模型；曹德胜等[5]运用模糊综合评价方法对备选雷达站进行初选，建立雷达站选址双目标模型，设计遗传算法求解；艾云飞等[6]建立雷达站选址-配置优化模型，赋予目标优先级并设计遗传算法求解。

综上所述，当前对VTS雷达站选址-配置问题的研究较少，方法较单一。由于雷达站选址-配置问题属于多目标优化的最小生成树(Minimal Spanning Tree, MST)问题，而交互式线性和通用优化求解器(Linear Interactive and General Optimizer，LINGO)是解决MST问题的一种有效方法，因此本文借助LINGO建立VTS雷达站选址-配置双目标优化模型来求解该问题。

1 LINGO介绍

LINGO是一种专门求解最优化问题的软件包，拥有一系列完全内置的求解程序[7]，主要功能包括构建线性、非线性和整数最优化模型、读取和写入Excel及数据库等。由于LINGO拥有方便构建和维护交互式模型、方便进行数据输入和输出选择及求解器功能强大等优势，使得其应用越来越广泛。诸如锚位数计算问题、旅行商问题(Traveling Salesman Problem，TSP)、最短路问题和物流配送中心选址问题等多目标规划问题都能通过LINGO得到解决或优化。[8-11]

2 VTS雷达站选址-配置问题描述

假设条件：

1) 随机划分若干个水域单元，各水域单元的重要程度已知。

2) 雷达有一定的作用距离，水域单元只有存在于该型号雷达的最大作用距离和最小作用距离之内，才能表示被覆盖。

3) 每个雷达站可建立点最多只能建立1个雷达站，且每个雷达站最多只能配置1种型号的雷达。

4) 不同雷达的检测稳定性不同，容易受天气、海况和地形等外界因素的干扰，使得其覆盖稳定性有一定的差异。需被多重覆盖的重点水域是指由于建筑物、岛屿等物体的遮挡而产生盲区，从而需多台雷达进行覆盖的水域。

5) 总成本包括雷达成本、雷达站建设成本和线路铺设成本。

3 VTS雷达站选址-配置优化模型建立

3.1 引入参数

E为水域单元编号,e=1,2,…,E;F为雷达站可建立点编号,f=1,2,…,F；H为VTS中心;Lf为f雷达站配置雷达的最大探测距离;lf为f雷达站的最小探测距离;Def为水域单元e与雷达站f之间的距离,当lf≤Def≤Lf时，水域单元e被雷达站f覆盖;Dfh为雷达站可建立点到VTS中心的距离;NF={f|lf≤Def≤Lf}为能覆盖水域e的雷达站集合;NE={e|lf≤Def≤Lf}为能被雷达站覆盖的水域单元集合;i为0-1变量，若水域单元e被覆盖2次以上，则ie=1,反之ie=0；j为0-1变量，若雷达站可建立点f被选中，则jf=1,反之jf=0；Yf为0-1变量，若选中f雷达站，且配备雷达，则Yf=1，反之Yf=0；qe为水域单元e的重要性，其大小反映水域单元是否被遮挡，需多重覆盖来消除盲区；Q为阈值，若qe≥Q,则水域单元e需至少覆盖2次；xe为水域单元e的船舶流量；Xf为雷达可建立点f配置雷达的最大监测能力；λf为雷达监测的稳定性；μe为水域单元e被监测的稳定性；Af为单个雷达站的建设成本；B为雷达站到VTS中心每公里线路的铺设成本；C为雷达的成本；δ为成本最小目标函数的优先度；1-δ为稳定性最高目标函数的优先度。

在当前大学教育强调全面发展和创新性思维阶段，以及高校建设“双一流”背景下，注重高校本科生毕业论文的选题，注重高校本科生专业综合素质能力的提升，既有助于提高大学生的职业生存能力和社会竞争力，也有利于促进高校审视学科发展和专业培养人才的模式，从而为国家和社会输送专业能力强、素质过硬、具有探索和创新精神的复合型人才。高校本科毕业论文的指导工作任重道远，仍然需要一线教学和教务人员不断探索和实践完善。■

3.2 建立模型

根据以上引入的变量建立目标函数，有

(1)

(2)

(3)

Z=δmin ∂+(1-δ)maxη

(4)

式(1)表示总成本最小，包括雷达成本、雷达站的建设成本和被选雷达站到VTS中心的线路铺设成本；式(2)表示水域单元被有效监测的稳定性；式(3)表示水域单元被有效监测的稳定性之和最大；式(4)表示赋予2个目标优先级。

模型的目标函数需满足约束条件

(5)

(6)

(7)

ie,jf,Yf∈{0,1}

(8)

式(5)表示每个水域单元至少被覆盖1次，即全面覆盖；式(6)表示由于建筑物、岛屿等原因存在雷达覆盖盲区的水域单元至少被覆盖2次，即重点水域的多重覆盖；式(7)表示水域单元的船舶流量不超过雷达站的最大监测能力；式(8)表示变量服从0-1约束。

4 LINGO实现的算例及分析

4.1 算例参数信息

假定将某港口水域划分为20个单元，各单元位置坐标已知。VTS雷达站可建立点有8个，位置坐标已知。VTS中心坐标已知。最多设立4个雷达站，每公里线路铺设成本为1，水域单元的重要度阈值为5。[12]水域单元参数见表1，VTS雷达站可建立点参数见表2，雷达参数见表3。

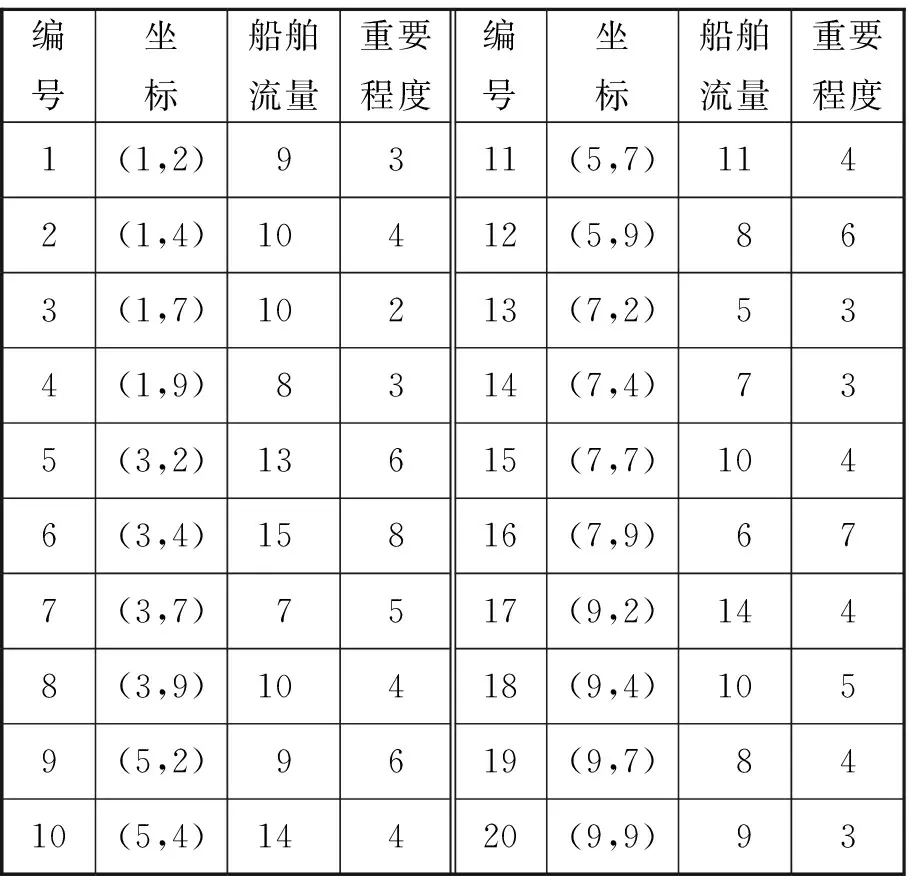
表1 水域单元参数

表2 雷达站可建立点参数

4.2 算例分析

运用LINGO求解模型，赋予双目标优先级。

1) 取δ=0.5，即双目标优先级相同。运行结果显示，1号、3号、5号和8号雷达站可建立点被选中，结果达到水域单元完全覆盖和因建筑物、岛屿等遮蔽而存在盲区的重点水域多重覆盖的目标。VTS雷达站建设成本为100.2，水域单元被监测的稳定性之和为42.5。VTS雷达站选址-配置结果见图2。各水域单元覆盖情况见表4。VTS中心坐标为(5,0)。

表3 雷达参数

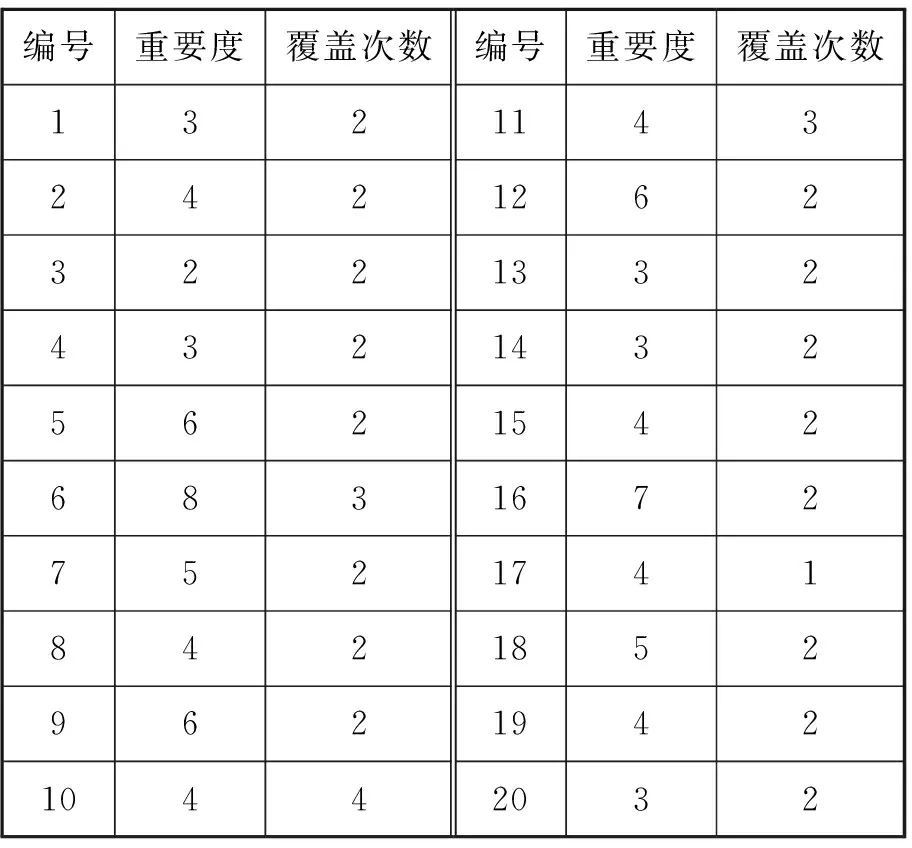
编号重要度覆盖次数编号重要度覆盖次数13211432421262322133243214325621542683167275217418421852962194210442032

2) 取δ=0.8，即成本目标优先于稳定性目标。运行结果显示，1号、4号、7号和8号雷达站可建立点被选中，结果达到水域单元完全覆盖和因建筑物、岛屿等遮蔽而存在盲区的重点水域多重覆盖的目标。VTS雷达站建设成本为98.4，重点水域多重覆盖的稳定性为36.9。VTS雷达站选址-配置结果见图3。各水域单元覆盖情况见表5。

3) 取δ=0.2，即稳定性目标优先于成本目标。运行结果显示，3号、4号、5号和6号雷达站可建立点被选中，结果达到水域单元完全覆盖和因建筑物、岛屿等遮蔽而存在盲区的重点水域多重覆盖的目标。VTS雷达站建设成本为107.6，水域单元被监测的稳定性之和为51.3。VTS雷达站选址-配置结果见图4。各单元水域覆盖情况见表6。

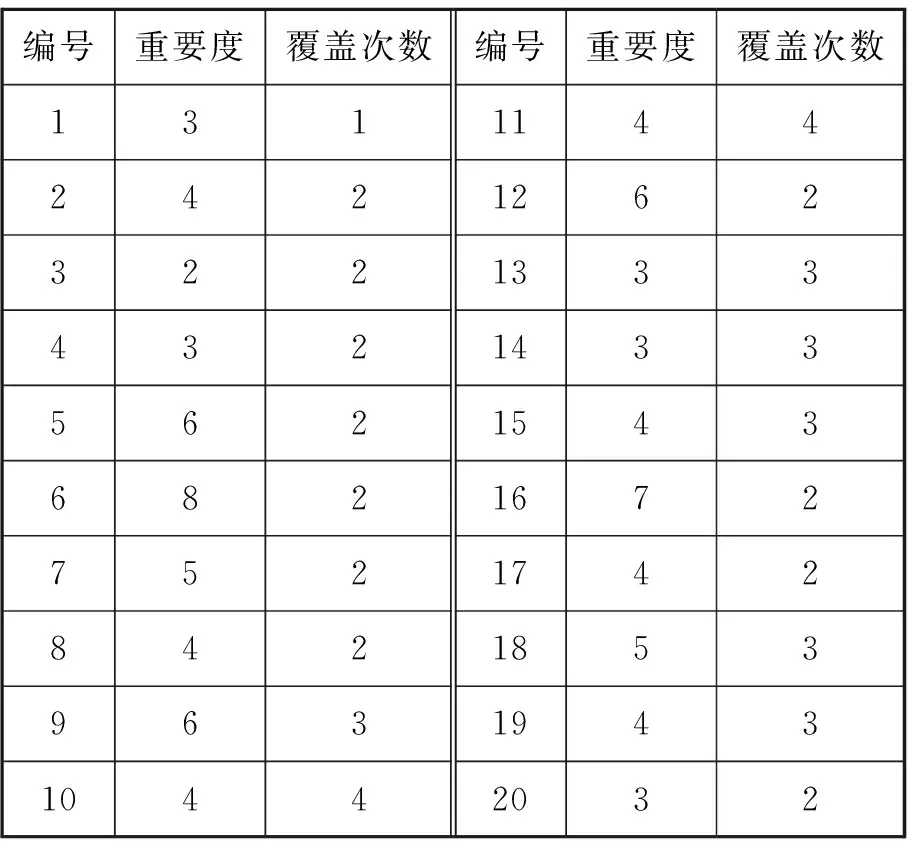
编号重要度覆盖次数编号重要度覆盖次数13111442421262322133343214335621543682167275217428421853963194310442032

通过3次运算发现，运行结果随着δ值的变化而变化，说明目标优先级会对选址-配置结果产生影响。为得到更可靠的结论，分别取δ=0,0.1,0.2,…,1.0，得到不同的选址-配置方案，运行结果见表7。

由运行结果可知，最终的方案均实现了水域单元的全面覆盖和因建筑物、岛屿等遮蔽而存在盲区的重点水域多重覆盖的目标。δ值不同，运行结果不同，说明双目标的优先级会影响最终的选址-配置方案，且随着δ值的不断增大(即成本目标的优先度越来越高，稳定性目标的优先度越来越低)，总成本和稳定性的变化基本上呈递减的趋势，符合模型假设和实际情况。将程序运行20次，结果稳定，说明模型具有可行性。

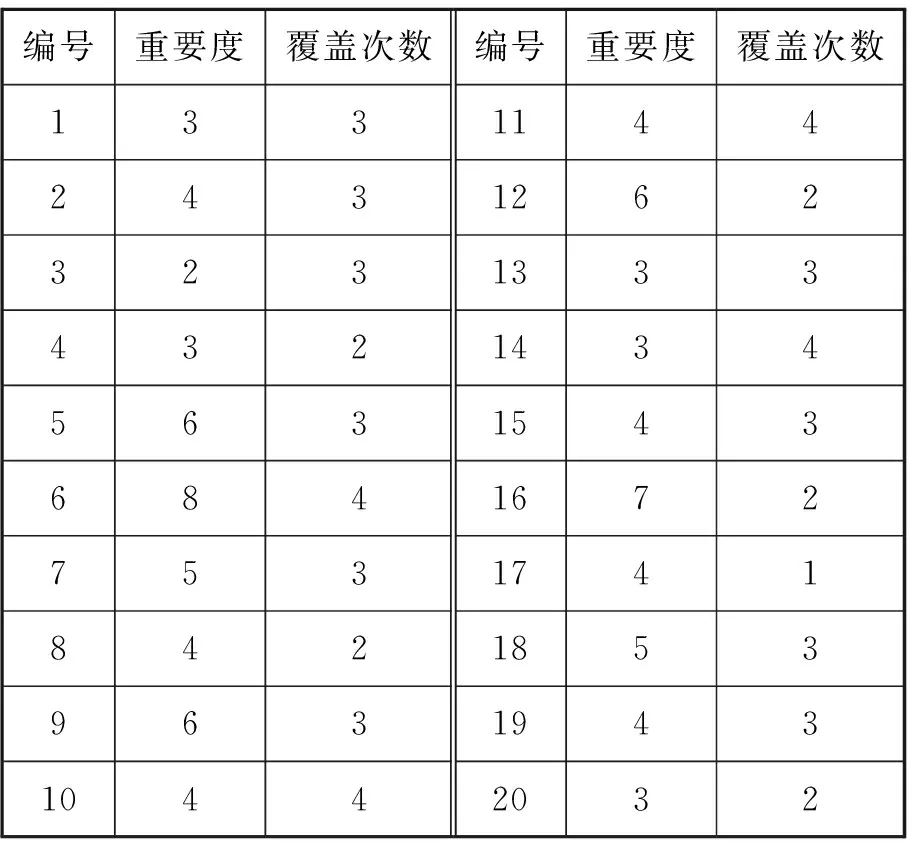
表6 δ=0.2时水域单元覆盖情况

表7 选址-配置结果

5 结束语

1)创新性地将LINGO引入到VTS雷达站选址-配置问题的求解中。运用LINGO建立双目标优化模型并求解出可靠运行结果。结果稳定，易于实现，模型具有可行性。

2)综合考虑水域遮蔽物、雷达盲区、雷达作用距离、建设成本和水域船舶流量对雷达选址-配置的影响，所得结果对实际工作中雷达的选址-配置有指导意义。在具体实施过程中，根据实际情况选择不同的优先级，实施不同的方案。

[1] 易中立. 基于宜昌VTS雷达站的船用雷达交管化研究[D].大连：大连海事大学,2010.

[2] TOREGAS C, SWAIN R, REVELLE C, et al. The Location of Emergency Service Facilities[J]. Operations Research, 1971, 19(6):1363-1373.

[3] CHURCH R L, MEADOWS M E. Location Modeling Utilizing Maximum Service Distance Criteria[J]. Geographical Analysis, 2010, 11(4):358-373.

[4] 史云剑. 谈VTS建设中雷达站的选址[J]. 航海技术,2005(6):37-38.

[5] 曹德胜,吕靖,艾云飞,等. VTS雷达站选址问题优化模型[J]. 北京航空航天大学学报,2014,40(6):727-731.

[6] 艾云飞,吕靖,张丽丽,等. VTS雷达站选址-雷达配置优化模型[J]. 中国航海,2014,37(4):54-58.

[7] 杨松姗,张金中.利用LINGO模型进行锚位数计算的探讨[J]. 港工技术, 2016,53(4):29-30.

[8] 吴希. LINGO软件在货物运输问题中的应用[J]. 中国商论,2016(25):71.

[9] 陈允峰. 利用lingo软件解决最短路问题的两种方法[J].信息技术与信息化,2015(10):141-142.

[10] 吴有平,刘杰,何杰. 多目标规划的LINGO求解法[J]. 湖南工业大学学报,2012,26(3):9-12.

[11] 徐丽蕊. 基于LINGO的城市物流配送路径优化[J].电子设计工程,2013,21(22):52-54.

[12] 曹德胜. 我国VTS绩效评价与雷达站选址研究[D].大连:大连海事大学,2014.