碰撞船舶的船体损伤对推进轴系的影响
董良雄, 施怡然, 杨 意
(浙江海洋大学 港航与交通运输工程学院,浙江 舟山 316022)
船舶在航行过程中遭遇的碰撞事故往往无法预测,且一旦发生就有可能使船舶遭受严重损伤,进而影响船舶推进系统,给船舶碰撞相关研究带来困难。对此,相关人员围绕船体的结构设计情况、船舶管理状态和船体二次损伤(因船体损伤使得艉轴发生碰摩,造成船体轴系损伤)状态进行数值模型分析研究。任孔愚[1]基于大量大型散货船体和沉船事故分析,给出船体结构设计缺陷部位和管理不善的解决方案;陈景杰[2]对船体损伤状况下的结构裂纹类型进行分析和研究,提出通过改善船体材料和增加材料硬度来缓解船体损伤带来的危害;姜金辉[3]分析船舶发生碰撞工况下船体部分结构的改善情况,有利于减弱船体的碰撞损伤。然而,这些研究只是对船体特性进行分析,未对船体损伤引起轴系损伤之后,因处理方式不当而使轴系受到二次损伤进行深入分析。对此,本文在船体损伤工况下,通过改变轴系支撑刚度来模拟实际工况下的不同船体损伤,以期得到不同船体损伤对船舶轴系运动特性的影响,从而减弱或预防船舶航行过程中因船体损伤带来的二次损伤及改进船舶发生意外事故之后的处理措施。
1 损伤船体轴系模拟试验台的构建和分析
船舶在航行过程中遇到风浪、触礁、碰撞或其他复杂环境时,可能会受到不同形式的损伤,这些不可预估的损伤会导致船舶轴系支撑轴承位置发生移动和相对刚度发生变化,并进一步反作用于船体上,造成船体发生耦合振动,对船体造成二次损伤。本文在船舶损伤工况下,通过对船舶轴系作离散化处理,运用弹簧和改变可变支撑刚度来模拟复杂船舶损伤下的轴系运动状态,探究推进轴系在船舶损伤工况下的运动特性。艉轴试验台结构见图1。
图1中:m1和m2为左右轴颈质量;m3和m4为前后艉部结构质量;m5为圆盘质量;c1为转轴在轴承处的阻尼系数;c2为转轴在圆盘处的阻尼系数;c3为艉部结构阻尼系数;k1为弹性轴刚度;k2、k3、k4、k5为前后艉部结构及连接刚度。
2 系统动力学分析模型
转子系统动力学方程为
(1)
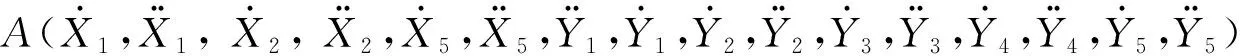
3 船舶损伤下轴系的动力学特性分析
船舶在受到意外损伤时可能会导致船体总体刚度发生变化,进而对推进系统的轴系支撑刚度造成影响,从而改变船舶轴系的运动状态。因此,本文模拟艉轴结构,通过对船体轴系支撑刚度进行一系列的分析,探究轴系在不同船体损伤工况下的运动特性和船体损伤之后如何有效减弱和避免二次损伤。
3.1 可变支撑刚度对艉轴运动特性的影响
在实际航行事故中,船体损伤情况及其给轴系支撑带来的损伤通常不同,因此会给实船轴系损伤研究带来困难。[4-9]本文通过改变船体轴系的支撑刚度来模拟不同工况下的船体损伤。对实船损伤下的轴系作数值分析模型处理,为相关人员分析此类问题提供方便。
取可变支撑k3的刚度为30×106N/m,在该情况下可近似认为模拟试验台支撑为刚性支撑,求解式(1),得到系统响应结果,绘出滑动轴承处的轴心振动分岔图(见图3)。同理,取支撑刚度分别为59×106N/m和88×106N/m,绘制出轴心振动分岔图见图3。
由图3a)可知:当艉轴在支撑刚度为30×106N/m的情况下运转时,转速处于较小的状态(100~150 rad/s),此时油膜力在转子运动过程中起主导作用。随着转速的增大,周期运动状态在150 rad/s转速下发生变化,运动状态变为倍周期运动,且一直持续到205 rad/s。在205~275 rad/s转速范围内,周期运动与倍周期运动交替出现;在570 rad/s转速时艉轴运动周期状态变为3T周期;在570~580 rad/s转速时为4T周期;在580~585 rad/s转速时变化为3T周期;在585~589 rad/s转速时为2T周期运动;在590 rad/s转速时达到周期运动之后进入倍周期运动。由图3d)可知:当转速在600~710 rad/s时,艉轴的运动状态发生较大的变化,由概周期运动转化为混沌运动。
由图3c)可知:当艉轴在支撑刚度为88×106N/m情况下运转时,转速处于较小的状态(100~147 rad/s),油膜力在转子运动过程中起主导作用,系统的稳态响应呈现为周期运动。随着转速的增大,周期运动状态在147 rad/s转速时发生变化,运动状态变为倍周期运动,且一直持续到147 rad/s,而在147~700 rad/s转速时为周期运动与倍周期运动交替出现,在700~749 rad/s转速时为4T周期运动,在750 rad/s转速时艉轴运动周期状态改变为3T周期运动,在751~800 rad/s转速时变化为4T周期运动。由图3e)可知,当转速为800~890 rad/s时,艉轴的运动状态发生较大的变化,转变为概周期运动,而在890 rad/s转速之后由概周期运动转化为混沌运动。
由图3可知,随着船体在损伤情况下的支撑刚度发生改变,船体的轴系系统运动特性也发生变化。例如:在图3a)中,当可变支撑刚度为30×106N/m时,艉轴的运动状态在711 rad/s转速时由概周期运动转化为混沌运动;在图3e)中,当可变支撑刚度为8.8×106N/m时,艉轴的运动状态在转速为890 rad/s时由概周期运动转化为混沌运动。
采用类似方法,观察可变支撑刚度变化对系统运动周期的影响,取艉部可变支撑k3的支撑刚度为1×106N/m、1.5×107N/m、3.0×107N/m、4.5×107N/m、5.9×107N/m、7.4×107N/m、8.8×107N/m和1.14×108N/m,在艉轴轴颈处模拟振动信号,绘出可变支撑刚度大小与临界转速进入混沌运动的关系见表1和图4。
从图4中可看出:在碰撞情况下,船舶轴系的支

表1 可变支撑刚度大小与临界转速进入混沌运动的关系
撑刚度会在一定范围内变化,并会对艉轴的运动特性产生影响:
1) 当支撑刚度为2.0×107~5.9×107N/m时,艉轴振动进入混沌运动的临界转速随着可变支撑刚度的增大而增大。
2) 当可变支撑刚度超过5.9×107N/m之后,可变支撑可视为刚性支撑,支撑刚度继续增大对艉轴进入混沌运动的临界转速的影响很小。
当船舶发生碰撞造成船体受损时,损伤越严重,轴系支撑刚度越小,艉轴进入混沌运动的临界转速越小。因此,应加大对船舶推进轴系的监测力度,同时适当降低航速,以减弱轴系进入混沌运动的趋势,避免轴系受到二次损伤。
3.2 船体在损伤情况下的力传递对艉轴系统的影响
当船体意外受损之后,船体轴系不仅会受到损伤,还可能因其他第二次外力传递受到二次伤害。因此,通过对船舶受损之后轴系的力传递进行研究,为实船损伤的轴系研究提供参考。基于模拟试验台可变支撑的应用,在图1中的m3处加入稳定荷载,通过对不同荷载下艉轴的振幅进行分析来研究船体损伤情况下轴系的力传递。取可变支撑k3的刚度为3.0×107N/m,加入荷载50 N、100 N、150 N和200 N绘制不同荷载下的艉轴振幅图(见图5,各荷载对应不同曲线)。
从图5中可看出:随着m5施加的外力荷载的增加,轴系的运动状态也发生变化:
1) 当在无外力荷载情况下运转时,轴系进入最小幅值的转速为810 rad/s,轴系最小振幅为0.38 mm,最大振幅约为0.85 mm。
2) 当外力荷载增加到50 N时,轴系进入最小振幅的转速为800 rad/s,此时最小振幅增大,但最大振幅减少到0.83 mm。
3) 当外力荷载增加到150 N时,轴系进入最大振幅的转速为750 rad/s,最小振幅约为0.37 mm,最大振幅为0.82 mm。
4) 当外力荷载增加到200 N时,最小振幅改变较小,仍为0.37 mm,在该阶段,外力荷载的增加对轴系运动特性的影响变小,说明此时轴系受到的损伤较为严重。
当船舶发生碰撞时,轴系支撑会因受到外力冲击而提前到达混沌运动状态(不稳定的运动状态),且随时可能使轴系出现剧烈振动或碰摩故障,导致“二次损伤”出现。因此,当船舶发生碰撞时,应合理地操船来减弱外力对船体轴系的损伤。
3.3 实船损伤下的轴系运动特性分析
通过上述数值模拟虽然能对船体损伤下轴系的运动特性进行仿真分析和研究,但因数值仿真精度等原因,与实船损伤下的轴系运动特性略有差异。因此,采用实船损伤轴系数据进行分析研究,以获取真实船体损伤情况下轴系的运动特性。
由文献[10]得知:因碰撞造成船体损伤之后,其前艉轴支撑刚度为7.276 2×108N/m,经造船设计单位提供,在正常运行时前艉轴支撑刚度为9.8×108N/m。基于该数据建立试验模型,取损伤前后可变支撑刚度分别为9.8×106N/m和7.2762×106N/m。取m3=50 kg,轴承外阻尼De=2×103N·s/m,轴承宽度l=0.102 m,轴承半径R=0.067 m,密封间隙c=0.003 m,分别在转速为270 rad/s、440 rad/s和708 rad/s时绘制分析图(见图6)。图6Ⅰ为根据式(1)的数值模拟结果所作的庞加莱映射图,由该图可更清楚地了解船舶损伤之后艉轴系统的周期性运动形态,将轴心的轨迹用一个截面横截,从而根据轨迹在截面上穿过的情况,简洁地判断轴心运动的周期性形态。图6Ⅱ为轴心运动轨迹;图6Ⅲ为艉轴在振动期间的时间历程;由图6Ⅳ可直观地观测出艉轴系统运动的周期数。
当航船处于低速航行状态且轴系转速为ω=270 rad/s时,在图6a)中,由图Ⅰ和图Ⅲ可知系统做4T周期运动,由此可观测出艉轴系统运动的频率为1/4T整倍频率,且由图Ⅰ可知系统此时映射为4个点。由图6b)也可观测到类似的4T周期运动状态,但通过对比2个庞加莱映射图可发现船体损伤下的轴心运动轨迹更加散乱。由此可知,在较低的转速范围内,虽然正常航船和损伤航船在一定转速内的运动周期性变化类似,但因船体损伤造成其运动轨迹不同。
当航船正常航行,且处于轴系临界混沌转速ω=708 rad/s时,在图6c)中:由图Ⅱ和图Ⅲ可知此时系统的状态发生较大的变化,系统此时的响应状态为混沌运动,图Ⅳ中出现多组不同频率值,图Ⅰ中的点数也剧烈增多,系统进入混沌运动状态。此时观测图6d)中的图Ⅰ和图Ⅱ可知,轴心的映射轨迹点更加混乱,且由图Ⅲ可知运动过程中艉轴振幅增加到0.86 mm(图6c)中的振幅约为0.85 mm),由此可知船体受损后轴系的混沌运动状态更加混乱,且有可能对轴系造成二次损伤。
综上所述,当损伤航船在较低的航速下运行时,可有效减弱船体轴系的混沌运动状态,从而降低推进轴系受到二次损伤的概率。当转速ω=270 rad/s时,正常航船与损伤航船的运动特性类似;当转速增加到正常转速ω=708 rad/s时,船体的损伤会加剧船体的混沌运动,从而可能导致轴系受到二次损伤。
4 结束语
船舶在航行过程中会因意外情况而受损,这些损伤可能会使船舶的各系统受到不同程度的损伤。本文基于船舶受损工况,对船体轴系运动特性进行分析和研究,试验结果表明:
1) 在船体受损工况下,艉部结构的运动状态会随着支撑刚度的改变而改变,同时轴系从概周期运动进入混沌运动的临界转速也会发生变化。当支撑刚度达到一定值之后,艉轴从概周期运动进入混沌运动时的临界转速趋于稳定。
2) 在船体受损工况下,因船体损伤而引起的轴系损伤会使船舶碰撞力的传递进一步加剧,相应地会再次作用在推进轴系上,造成二次损伤。因此,在船舶受损状态下,应采取措施地对船舶推进轴系进行保护。
3) 在船体受损工况下,应通过降低转速(如转速为100~708 rad/s较为合理)来保护轴系的运转,以避免或减弱轴系在运行中因转速过高而受到二次损伤。
[1] 任孔愚.大型散货船船体损伤事故及对策研究[J].中国航海, 1996(1):44-55.
[2] 陈景杰.含裂纹损伤船体结构强度分析方法研究[D].大连:大连理工大学, 2011.
[3] 姜金辉,王自力.船舶碰撞同步损伤过程研究[J].智能制造, 2005(6):53-55.
[4] 王正浩,刘大任,尹晓明.转子系统拟周期演变为混沌运动过程分析[J].沈阳建筑大学学报(自然科学版), 2008, 24(4):688-693.
[5] 秦丽.大型船舶推进轴系功率流分析理论与方法研究[D].武汉:武汉理工大学, 2014.
[6] 李忠刚.含转子-轴承-密封系统非线性动力学特性的研究[D].哈尔滨:哈尔滨工业大学, 2007.
[7] VERKO D, ESTAN. Experimental Determination of Stern Tube Journal Bearing Behaviour[J].Brodogradnja, 2010, 61(2):130-141.
[8] LIU Changqing, CHE Chidong, SHEN Xiaohan. Experimental and Numerical Study on Vibration of the Full-Revolving Propulsion Ship Stern[J].China Ocean Engineering, 2015, 29(1):33-48.
[9] LEE T G, KIM J H, JO D H. Composition Containing Inorganic Nanoparticles as an Active Ingredient for Preventing or Treating of Angiogenesis Related Diseases: US9238006[P]. 2016.
[10] 蒋平. 多因素综合效应下大型船舶轴系校中研究[D]. 武汉:武汉理工大学, 2012.

