电力推进船舶复合储能装置容量多目标优化

杨祥国， 孙 盼， 杨 诚， 陈 辉， 孙 俊,杜 枢， 赵霏霏， 杨 凌， 魏斯琦

(1.武汉理工大学 能源与动力工程学院， 武汉 430063；2.中国核动力研究设计院设计所， 成都 610041;3.四川省林业科学研究院， 成都 610066；4.中国电子科技集团第二十九研究所， 成都 610036)

带储能装置的某耙吸式电力推进挖泥船的电力推进系统结构见图1。由图1可知，该挖泥船主要由2台柴油发电机组、2台泥泵、双螺旋桨和其他负载组成。超级电容组和蓄电池组组成复合储能装置，并通过多端口DC/DC变换器与直流母线相连。电力推进船舶运行时的稳定性和经济性与复合储能装置的容量息息相关。

复合储能装置综合效益的发挥与复合储能装置中各储能单元的配比是否合理直接相关。因此，对复合储能装置进行优化配置是复合储能装置在船舶电力推进系统中应用的关键技术之一。[1-4]

目前，针对复合储能装置优化配置的研究大多基于微电网，且通常局限于从单一目标函数对复合储能装置进行容量配置，只考虑应用的某一方面。然而,复合储能装置兼具多种功能，在不同场合对其容量配置的要求存在较大差异。[5-6]若只从某一方面考虑储能装置的容量配置，难以综合发挥最优功效，因此复合储能装置容量的优化配置是一个多目标优化问题,应综合考虑成本、功率平衡、功率平抑和储能装置使用寿命等因素。[7-9]

图1 带储能装置的某耙吸式电力推进挖泥船的电力推进系统结构

1 船舶电力推进系统复合储能装置容量配置的优化建模

1.1 船舶电力推进系统复合储能装置容量配置的优化目标

1.1.1成本目标

成本目标是在满足功能需要的基础上降低成本。复合储能装置的成本目标函数应考虑超级电容和蓄电池的单位容量价格、储能容量、能量转化率及维护成本。[10]对此，建立成本目标函数f1，有

f1=cbEb/ηb+ccEc/ηc+cmPtotal

(1)

式(1)中:cb和cc分别为蓄电池和超级电容的单位容量价格；Eb和Ec分别为复合储能装置中蓄电池和超级电容需优化配置的容量；ηb和ηc分别为蓄电池和超级电容的能量转化率；cm为复合储能装置的维护成本；Ptotal为复合储能装置的总功率。

1.1.2负载功率波动平抑目标

电力推进船舶的负载随工况的变化而变化，负载的不断变化将导致船舶电网产生波动，降低船舶运行的可靠性和安全性；同时，该波动会迅速响应到柴油发电机组，使其偏离最佳工况，经济性降低，排放量增加。为表征储能装置对负载功率波动的平抑效果，以平抑之后船舶负载功率变化差的平方和最小为原则建立目标函数。[11]设定储能装置参与平抑负载功率波动的时间为[t11,t12]，目标函数f2为

(2)

(3)

1.1.3船舶电力推进系统供求平衡目标

对于装载复合储能装置的船舶电力推进系统，要确保任意时刻功率供求平衡。若储能装置容量不足，可能会出现柴油发电机组发电浪费、复合储能装置不能很好地平抑负载功率波动等现象，从而造成船舶运行的可靠性降低、经济性下降；若储能装置容量过大，不仅会严重增加成本，而且可能导致储能装置的使用率降低，影响其性能和使寿命。[12]对此，需建立经过储能装置补偿之后推进系统的供求平衡目标函数。目标函数以各时间段船舶的实际输出功率与补偿之后的输出功率均值偏差的平均和最小为原则，设定储能装置参与供求平衡补偿的时间为[t21,t22]，目标函数f3为

(4)

(5)

式(4)和式(5)中:PO,i为第i时间段内实际的船舶负载功率；Pavg为经复合储能装置平抑之后船舶负载功率的供求差异平均值。

1.2 船舶电力推进系统复合储能装置目标优化的约束条件

对于船舶电力推进系统中复合储能装置的容量优化，在考虑优化目标的同时，还要考虑船舶电力推进系统的能量约束、瞬时功率平衡和储能装置中各储能单元的荷电状态、最大功率限幅等方面的约束，从而保证储能装置容量优化的合理性。[13]

1.2.1能量约束

在船舶电力推进系统中，复合储能装置不仅需满足输出功率的要求，而且需拥有足够的输出能量来满足系统的最大实际需求。

(1)任意时刻蓄电池的储能为

Eb,i+1=Eb,i+ΔEb,i=Eb,maxSOCi+Pb,iT/r

(6)

(2)任意时刻超级电容的储能为

Ec,i+1=Ec,i+ΔEc,i=Ec,i+Pc,iT

(7)

式(6)和式(7)中:ΔEb,i为蓄电池的能量变化量;ΔEc,i为超级电容的能量变化量；Eb,max为蓄电池的额定容量；T为控制周期；r为匹配常数；Pb,i为蓄电池的补偿功率;Pc,i为超级电容的补偿功率;SOCi为荷电状态。

要满足控制周期内船舶电力推进系统最大负载能量的变化量，即

ΔEb,i+ΔEc,i≥ΔEmax

(8)

1.2.2瞬时功率平衡约束

船舶在实际运行时，负载的负荷会随环境和外界条件的变化而变化,但整个电力推进系统的功率必须在任意时刻都处于平衡状态，否则会造成能量的浪费，降低能量使用率。该平衡方程为

(9)

在任意时刻，复合储能装置通过充放电来维持电力推进系统的功率稳定，放电时Pb,i和Pc,i为正，充电时Pb,i和Pc,i为负。

1.2.3复合储能装置中储能单元荷电状态SOC的约束

储能单元的过充过放都会造成储能装置的使用寿命缩短、维护成本增加。对此，通常采用荷电状态(SOC)作为衡量储能装置在充放电过程中是否存在过充和过放情况的指标。荷电状态是指储能装置在充放电结束之后剩余容量与额定容量之比，即

(10)

式(10)中:k为储能装置的类别(超级电容或蓄电池)；Eini为储能单元在充放电前的初始容量；ηch和ηdis分别为储能单元的充放电效率；Pch和Pdis分别为储能装置的充电功率和放电功率；t为充放电的时间；Er为储能单元的额定容量，即需优化的容量。

在储能装置实际使用过程中，其储能荷电状态SOC的上下限并不是理想的0和1，而应根据实际情况进行约束，防止储能单元出现过放情况。因此，在任意时刻都必须对复合储能装置中蓄电池和超级电容的荷电状态SOC的上下限进行严格控制，即

SOCmin≤SOCi≤SOCmax

(11)

1.2.4最大瞬时功率的约束

电力推进船舶作业过程不仅存在负荷突变的情况，而且可能发生电机短路、柴油发电机失效等机械故障。这就需复合储能装置能迅速输出较大的功率对其进行补偿。为避免船舶运行中因机械故障而工作异常，复合储能装置输出的总功率要大于等于最大负载瞬时功率的变化量,即

Pb,i+Pc,i≥ΔPmax

(12)

1.3 船舶电力推进系统复合储能装置的多目标优化数学模型

由以上分析可得出船舶电力推进系统复合储能装置容量优化配置的多目标数学模型，目标函数的数学模型和约束条件的数学模型分别为

(13)

(14)

2 船舶电力推进系统复合储能装置多目标优化方法

船舶电力推进系统复合储能装置的优化配置具有多个优化目标。与单目标优化相比，多目标优化需同时优化多个目标，这些目标之间往往相互矛盾且不兼容，某个优化目标性能的提高可能会导致其他优化目标性能的下降。因此，多目标优化的难度远远高于单目标优化。[14]这里采用自适应惯性权重的粒子群算法对船舶电力推进系统复合储能装置的容量进行多目标函数的寻优，寻找出复合储能装置超级电容和蓄电池的最优容量。

1)根据船舶电力推进系统复合储能装置的性能要求建立多目标函数。

2)根据各目标函数在整个系统中的重要程度，利用适应度离差排序法确定各目标函数的权重，并采用线性加权和法将多目标函数聚合成一个单目标函数。

3)利用自适应惯性权重粒子群算法对复合储能装置超级电容和蓄电池的容量进行寻优。

2.1 适应度离差排序法

多目标函数中各子目标函数在整个系统中的重要程度用权重系数λi表示，λi越大则子目标函数越重要，反之子目标函数的重要性越低。权重系数的选取关系到各目标函数的协调性和整个系统的综合性能，这里采用适应度离差排序法确定权重系数。

离差反映的是估计量与实际量之间的距离，用单项数值与平均值之差表示。对于船舶电力推进系统复合储能装置，离差为储能装置特定容量的储能值与最优值下的目标适应度值的差值，即

δij=fij-fij,i,j=1,2,…,m

(15)

式(15)中:fij=fi(xj)为储能装置在不同配置下目标函数的适应度值；fii为该目标函数在最优化配置下的函数值；m为多目标函数中目标函数的个数。离差越小,说明储能装置的容量配置与最优配置越接近；离差越大,说明两者的差值越大。

适应度值离差排序法的一般步骤为：

1)分别求出多目标函数中各子目标函数的最优解，记为xj。

2)将各子目标函数的最优解xj代入每个目标函数，从而得到相应目标函数适应度值,即

fij=fi(xj),i,j=1,2,…,m

(16)

3)求取不同最优解时各目标函数适应度值的离差,有

δij=fij-fii,i,j=1,2,…,m

(17)

由于fii为某目标函数的最优解(即最小值)，因此离差恒为非负值。

4)求取每个目标函数的离差均值(平均离差),有

(18)

由于δii=fii-fii=0，因此离差均值按(m-1)求取。

5)求取权重系数,有

(19)

由步骤3)可知离差恒为非负值，因此各子目标函数的权重系数都为非负值，且各子目标函数的权重系数的和为1。

6)构造新的目标函数,有

fi

(20)

构造原则为：均差较大的目标函数与较小的权重系数相乘;均差较小的目标函数与较大的权重系数相乘。

2.2 线性加权和法

船舶电力推进系统复合储能装置的容量优化是一个多目标优化问题，具有多个优化目标。线性加权和法即在考虑约束条件的情况下，将这几个优化目标按照其在系统中的重要程度分别乘上相应的权重系数λi，并满足权重系数的和为1，随后进行叠加，从而得到一个单目标函数。

fi(x),x∈X

(21)

式(21)中:X为在满足约束条件的情况下，目标函数可行解的范围；m为目标函数的个数。

3 自适应惯性权重粒子群优化算法

3.1 粒子群优化算法

20世纪90年代，KENNEDY等[15]根据鸟群的觅食行为提出粒子群算法(Particle Swarm Optimization，PSO)。粒子群算法从随机解出发，通过迭代对目标函数进行寻优。

假设一个群体P由n个粒子组成，这些粒子都以一定的速度在一个D维空间内飞行。将这n个粒子表示为x={x1,x2,…,xn}，将其速度表示为v={v1,v2,…,vn}；可用向量X=(xi1,xi2,…,xiD)表示各粒子在空间内的D维位置。在算法中，粒子在飞行过程中不断搜索和调整自身的位置和速度，第i个粒子的速度为V={vi1,vi2,…,viD}，自身经历的最优位置为pi={pi1,pi2,…,piD}，粒子群所经历的全局最优位置为gi={gi1,gi2,…,giD}。粒子的位置和速度的更新公式[5-6]为

(22)

式(22)中:d为空间的维数D；w为动态惯性权重；c1和c2为学习因子，为非负常数，其作用是调节粒子自身的最优位置pi与全局最优位置pg的牵引力度；r1和r2为0～1内的随机数；t为迭代次数。

粒子在D维空间内的搜索过程见图2。粒子更新速度vt+1，id主要由粒子的原始速度vt,id、自身的思考和学习其他粒子经验的过程等3部分决定。粒子的原始速度vt,id具有局部搜索和平衡全局的能力，局部搜索能力和全局搜索能力与vt,id的大小有关。vt,id大,则全部搜索能力弱，局部搜索能力强；vt,id小,则局部搜索能力弱，全局搜索能力强。粒子自身的思考表示粒子自身经验对当前搜索倾向的吸引程度，是对粒子自身所累积经验的利用，受c1r1的随机调整，可避免出现局部极小的情况，提高粒子的全局搜索能力。粒子学习其他粒子经验的过程与种群的领域拓扑结构和群体全局最优位置pg直接相关，受c2r2的随机调整，表示粒子之间的相互协作和信息共享。在这3部分的共同作用下，粒子根据自身经验并利用信息共享机制不断调整自己的位置和速度，从而得到最优的位置和速度。[16]

3.2 自适应惯性权重粒子群优化算法

在自适应惯性权重粒子群优化算法中，惯性权重w起到至关重要的作用，影响着全局搜索能力和局部收敛效果。当惯性权重w较小时，当前局部区域的搜索更加精确，从而有助于提高算法的局部搜索能力；当惯性权重w较大时，算法更易跳出局部极小点，从而有助于提高算法的全局搜索能力。

自适应惯性权重粒子群优化算法可根据目标函数值的变化自适应地调节惯性权重w。若目标值趋于局部优化，则惯性权重w增大；若目标值较为分散，则惯性权重w减小，从而维持搜索范围与搜索精度之间的平衡。惯性权重w进行自适应调节的计算式为

(23)

式(23)中:wmax和wmin分别为惯性权重w的最大值和最小值;f，favg和fmin分别为粒子当前目标值、平均目标值和最小目标值。其求解的流程见图3。

4 计算结果及分析

由于挖泥船通常在内河运行和作业，在正常航行时负载的扰动比在进行挖泥作业时的小很多，因此采样挖泥作业时负载的变化进行计算。某艘负载额定功率为13.2 MW的耙吸式挖泥船在一个作业周期(6 h)内的实际负载功率变化曲线见图4。

由图4可知，挖泥船在作业时，其负载功率变化很频繁，最大可在瞬间达到额定功率的70%。利用采样的负载功率曲线求平均值可得船舶的平均负载功率为5 353 kW。假设在加载复合储能装置之后船舶的负载功率稳定为5 353 kW，则船舶负载的功率波动为0，目标函数f2可忽略不计，变成求解成本目标f1和供求平衡目标f3这2个目标函数。将式(4)～式(10)代入到目标函数和约束条件中，可得到与容量相关的函数，设定超级电容的最大功率为5 MW，蓄电池的最大功率为4 MW；超级电容的荷电状态的最大值为0.9，最小值为0.1，初始值为0.5；蓄电池荷电状态的最大值为0.8，最小值为0.2，初始值为0.5；超级电容成本为20 000元/(kW·h)，蓄电池成本为1 800元/(kW·h)；超级电容的能量转换效率为0.95，蓄电池的能量转换效率为0.85。由于以船舶的一个作业周期来计算，计算时间相对较短，因此复合储能装置的维护成本可视为0。

在采用自适应权重粒子群算法进行计算时，设粒子数为18，学习因子均为2，最大惯性权重系数为0.9，最小惯性权重系数为0.4，迭代次数为250次，可得目标函数f1和目标函数f3的寻优结果见表1。

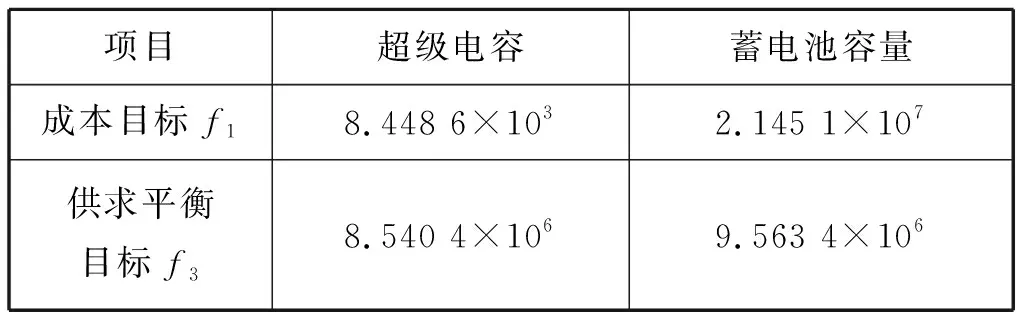
表1 成本目标函数和供求平衡目标函数的寻优结果 W·h

由表1可知:不同的目标函数对超级电容和蓄电池的容量需求差别很大，成本目标是从降低成本的角度考虑，希望蓄电池容量较大，超级电容容量较小；而供求平衡目标则是在满足功率平衡需要的前提下，两者的容量越大越好。

将各目标函数的最优容量解代入到式(16)中求解各目标函数相应的适应值，结果见表2。

表2 各目标函数在不同最优容量解下的适应度值

将利用式(16)求得的各适应度值代入到式(17)和式(18)中,求取各目标函数的离差和平均离差，结果见表3。

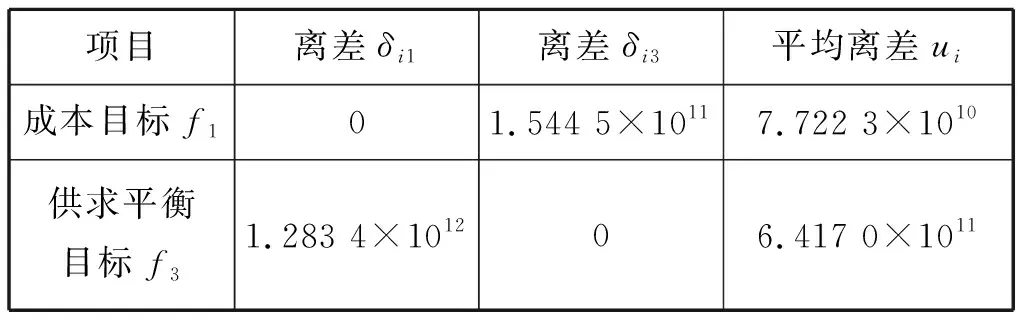
表3 各目标函数的离差和平均离差

表3中:离差越大,说明距离优化结果越远。由式(19)可得到新的权重系数，根据各目标函数的重要程度对权重系数的重要性重新排序，取λ1=0.893，λ3=0.107，λ2=0，则由式(20)可构造新的目标函数f为

(24)

对式(24)进行自适应粒子群优化，迭代次数为50次，目标函数的适应值与迭代次数的寻优关系见图5。

由图5可知，目标函数的适应值会随迭代次数的增加而快速收敛,并在迭代次数超过35次之后保持不变，得到最优适应值为4.256 4×1010。超级电容和蓄电池的容量与目标函数f的关系见图6。

由图6可知，超级电容和蓄电池的容量随目标函数值的变化而不断改变，并最终收敛于最优容量位置,其中超级电容的最优容量为5.283 4×105W·h，蓄电池的最优容量为2.091 2×107W·h。

5 结束语

本文建立复合储能装置容量配置的多目标模型和约束条件模型，并将自适应权重粒子群优化算法与适应度离差排序法相结合对复合储能装置的容量进行优化配置,能很好地发挥出复合储能装置在船舶电力推进系统中应用的综合效益，避免容量过大或过小带来经济性损失和安全性降低等问题。

[1] 陈晨, 王锡淮, 肖健梅. 储能单元在船舶电力推进系统中的应用[J]. 中国航海, 2014, 37(4):25-29.

[2] LINDTJØRN J O , WENDT F, GUNDERSEN B, et al. Demonstrating the Benefits of Advanced Power Systems and Energy Storage for DP Vessels[C]//Dynamic Posi-tioning Conference,2014:14-15.

[3] 陈晨, 王锡淮, 肖健梅. 含储能单元的船舶电力推进系统仿真[J]. 计算机仿真, 2015, 32(1):388-391.

[4] 李勇. 电力推进系统直流储能方法研究[J]. 上海船舶运输科学研究所学报, 2013, 36(4):20-23.

[5] 李成，杨秀，张美霞，等．基于成本分析的超级电容器和蓄电池混合储能优化配置方案[J]．电力系统自动化，2013,37(18)：20-24．

[6] 谢石骁，杨莉，李丽娜．基于机会约束的混合储能优化配置方法[J]．电网技术，2012,36(5)：79-84．

[7] 刘雨声, 鄂飞, 冯昊,等. 破冰船电力推进系统储能容量的优化配置[J]. 上海船舶运输科学研究所学报, 2016, 39(3):47-51.

[8] 郭力, 刘文建, 焦冰琦,等. 独立微网系统的多目标优化规划设计方法[J]. 中国电机工程学报, 2014, 34(4):524-536.

[9] 谭兴国, 王辉, 张黎,等. 微电网复合储能多目标优化配置方法及评价指标[J]. 电力系统自动化, 2014, 38(8):7-14.

[10] 冯江霞, 梁军, 张峰,等. 考虑调度计划和运行经济性的风电场储能容量优化计算[J]. 电力系统自动化, 2013, 37(1):90-95.

[11] 洪海生, 江全元, 严玉婷. 实时平抑风电场功率波动的电池储能系统优化控制方法[J]. 电力系统自动化, 2013, 37(1):103-109.

[12] 易林, 娄素华, 吴耀武,等. 基于变寿命模型的改善风电可调度性的电池储能容量尤化[J]. 电工技术学报, 2015, 30(15):53-59.

[13] 谢石骁, 杨莉, 李丽娜. 基于机会约束规划的混合储能优化配置方法[J]. 电网技术, 2012, 36(5):79-84.

[14] 谭兴国．微电网复合储能柔性控制技术与容量优化配置[D]．济南：山东大学，2014．

[15] KENNEDY J, EBERHART R. Particle Swarm Optimization[C]//IEEE Int Conf on Neural Networks, Perth, Australia, 1995. USA, 1995: 1942-1948.

[16] ZHANG L H, HU S. A New Approach to Improve Particle Swarm Optimization[C]//Lecture Notes in Computer Science, Chicago 2003, USA. Berlin, Germany: Springer-Verlag, 2003: 134-139.