海上风电场区船舶A*避碰寻路算法

薛双飞， 谢 磊， 王树武， 夏文涛， 包 竹

(1.武汉理工大学 能源与动力工程学院，武汉 430063； 2.国家水运安全工程技术研究中心，武汉 430063)

受传输效率和施工难度影响，目前海上风电场的建设大多集中在近海。然而，风电机组的布置通常需占用大片海域，风电场区及其附近的船舶若不能按照合理的路径航行，容易与风电机碰撞，造成风机受损、船舶遇险等事故。随着风力发电技术逐渐成熟，海上风电场的数量和装机规模将不断增加，这势必会影响近海船舶的安全航行。因此，研究在风电机组障碍环境下的船舶避碰航线设计具有重要意义。

船舶避碰航线可参考路径规划方法设计。按照对环境感知情况的不同，路径规划可分为全局路径规划和局部路径规划2类。全局路径规划即掌握全部环境信息，该方法适用于只有在静态障碍物的环境中；而局部路径规划中的环境信息部分未知，该方法适用于动态路径规划。由于风电机通常安装在海上固定的位置，其对船舶航行的影响可认为是已知的，因此船舶在风电场区的路径规划问题属于全局路径规划问题。

A*搜索算法是全局路径规划方法的一种，该算法简单易实现，并能保证全局最优解的收敛性。[1]A*寻路算法过程可分为环境构建、路径点生成和路径优化等3部分。

环境构建就是选择合适的方法描述障碍物信息，是路径规划和解决避障问题至关重要的一环，决定路径的优劣。[2]为方便确定障碍物的位置，现有的A*算法大多采用栅格法将环境信息分割为小方格，若小方格中包含障碍物，则将该方格标记为1(表示不可通过)，否则标记为0(表示可通过)。栅格法不仅可用来标识实体障碍物占有的空间，还可根据障碍物影响特征表示其影响范围，使目标不到达该领域。[3]然而，该方法也存在缺陷，即：格子的存在使得路径不能向任意方向延伸；同时，栅格的细化程度严重影响着算法的复杂度和发现路径的能力。郭耕辰等[4]提出的自适应分片算法在一定程度上突破了格子的限制，但依旧需采用栅格地图来描述环境。

根据环境地图的不同，A*算法生成路径点的方法也存在差异。一般情况下，A*算法采用4邻域节点扩展法或8邻域节点扩展法搜寻下一个最优节点位置。扩展节点的扩充能在一定程度上增加路径的自由度，但会使计算量成倍增加。为提高运算速度，一种稀疏A*算法[5]得到广泛应用，该方法通过在搜索中加入约束条件，有效裁剪搜索空间内的无效点。基于可视图的A*算法[6]也能提高路径规划速度，将当前点、障碍物各顶点和目标点组合连接，保证这些直线均不与障碍物相交，从而获取规划路径。

一般而言，利用A*寻路算法得到的路径是连接一系列散点生成的，在实际中若严格遵循该规划路径，需频繁改变方向，这样就造成方案的灵活性不足。为使A*算法规划出的路径有更强的实用性，单伟等[7]以位置、曲率和斜率作为路径平滑的标准，引入极多项式曲线生成平滑路径，使该路径同时满足机器人几何学特性和动力学特性。该方法可规划出平滑路径，但该路径不能保证远离障碍物。与之相比，基于A*路径规划的关键点优化法能在保证路径安全的同时实现路径平滑。[8]

针对现有A*算法中0-1地图不能准确描述船舶避碰过程的问题，首先在各风机位置已知的情况下，根据船舶避碰要求建立风电场区航行危险度地图；然后利用改进的A*算法，采取8领域节点扩展法生成路径点，初步规划风电场区船舶安全航行路径；最后提取路径拐点，并进行通视性检验，剔除非关键点，进一步使所得路径符合实际情况。

1 风电场区威胁势场建模

风电机组在海面上作为固定障碍物影响着附近船舶的安全航行，船舶需实时评估其所在位置的碰撞风险并及时对航线进行调整，以避免事故发生。风电场区的船舶碰撞风险可通过建立障碍物威胁势场来描述，决定威胁势场大小的因素主要有船舶与风机之间的距离和由于风机遮挡造成的船舶附近雷达阴影区面积2个。

1.1 风机威胁势场

船舶距离障碍物越近，与障碍物发生碰撞的概率就越大，这种关系可用人工势场理论来描述。传统人工势场法中存在斥力场和引力场，目标点对船舶有引力，而障碍物生成斥力。船舶在合力作用下移动，就能不断靠近指定位置。[9]

在对风机势场建模时，只考虑障碍物产生的势力场，按传统人工势场法可得斥力函数为

(1)

式(1)中:kb为斥力增益系数；d为船舶与障碍物之间的距离；d0为障碍物斥力场的作用距离。

对应的斥力为斥力函数的负梯度，其表达式为

(2)

式(2)中：X为船舶当前的位置向量。

上述方法中斥力为矢量，这就可能导致在多障碍物环境下，船舶所受斥力随着与障碍物间距离的减小而减小(见图1)。

显然，这种情况违背了船舶距离障碍物越近，碰撞危险越大(即障碍物威胁势场值越大)的要求。因此，为建立符合障碍物威胁势场性质的模型，需对传统人工势场进行改进。这里简单地用标量表示人工势场中的障碍物斥力，各点的威胁值是多障碍物在此处威胁值的叠加。于是单个障碍物产生的斥力表示为

(3)

由此可得多障碍物下的斥力大小见图2。

1.2 他船威胁势场

在评价风电场区船舶航行的安全性问题时，除了考虑船舶与风机的碰撞风险以外，还要考虑他船与本船的碰撞风险。风机的遮挡使得雷达不能探测到其阴影区内的船舶，因而雷达阴影区随时可能有船舶驶出，威胁本船的航行安全。考虑到风机对雷达电磁波的散射中有80%来自于风机塔身，每个风机叶对电磁波的散射量仅占散射量的5%，且出现在观测雷达位于风机正面或背面的情况下，因此在计算风机遮挡时，可只考虑风机塔身对雷达电磁波的遮挡。

阴影区对船舶航行安全的度量可用遮挡角表示。由于雷达波可认为沿直线传播，在分析遮挡角时，连接船舶与风机两侧所得夹角即为遮挡角α。雷达遮挡角示意见图3。

图3中：O为雷达位置；M为风机中心；r为风机半径；A和B为两处临界目标位置；d为船舶与风机间的距离。由此，遮挡角α的计算式为

α=2arcsin(r/d)

(4)

将船舶与风机间的距离和遮挡角大小一一对应，可评估各位置不可见目标造成的碰撞威胁Fship为

Fship=kα

(5)

式(5)中：k为比例系数，实现从遮挡角到碰撞威胁的转换。到风机的距离与风机遮挡角之间的关系见图4。

2 基于威胁势场的A*算法

搜索地图是影响采用A*算法设计避碰航线效果的重要因素，若能在地图中将约束条件详细地描述出来，便可设计出符合需求的最优路线。由于采用栅格化地图便于确定障碍物和规划对象的位置，因此该方法被广泛应用。

2.1 他船威胁势场

传统栅格化地图中的小方格只存在被标记为障碍物和可行区2种状态，其弊端是得到的航线可能沿着障碍物边缘或扩展的障碍物边缘。本文综合考虑风机威胁势场和船舶威胁势场，使航船与障碍物保持安全距离。

以包含34座风机的上海东海大桥海上风电场一期工程为研究对象(取左上角坐标为(121.95°W，30.82°N)、右下角坐标为(122.04°W，30.72°N)的矩形区)。在该区域航行的船舶多数为长约100 m的小型船舶，因此用100 m×100 m的方块将该区域栅格化。根据小方格相对于风机的位置和遮挡角即可量化该碰撞威胁。任意小方格的总威胁Ftotal是风机威胁Ffan与他船威胁Fship的和，可表示为

(6)

式(6)中：m和n为在影响范围内的风机数。

无论是与风机避碰还是与他船避碰，船舶与障碍物都应保持安全距离。当船舶与障碍物的距离小于安全距离时，船舶将主动远离障碍物，即此时障碍物威胁势场发挥作用。本文中该安全距离参考船舶安全领域要求取值，风机影响范围取半径为7倍船长的圆形区域，被风机遮挡的他船影响范围取半径为14倍船长的圆形区域。[10]

若以长为100 m的船舶为研究对象，则风机威胁势场模型中的d0取值700 m，另取斥力增益kb=10，此时单风机威胁值范围为0～10；而他船威胁势场中取比例系数k=100，此时单风机遮挡影响的他船威胁值范围为3～10。

根据以上约束条件，对各小方格进行计算之后得到的威胁地图见图5，颜色越深表示该处威胁度越大。

2.2 避碰路径点生成

A*算法的核心在于设计一个符合特定问题需求的代价函数[11]，可表示为

f(n)=g(n)+h(n)

(7)

式(7)中：f(n)为从出发点到终点路径上的代价值，在符合航行要求的情况下，f(n)越小，得到的路径越优；g(n)为从起点到当前点n产生的实际代价，是已有各路径点的累积和；h(n)为从当前点到终点代价的估计，又称启发函数，作用是引导路径点不断地接近最终目标。

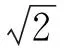
g(n)=g(n-1)+G+T(n)+Ftotal(n)

(8)

估价函数h(n)是保证找到最佳路径的关键影响因素之一。当估价值h(n)小于或等于当前点到目标节点的距离实际值时，搜索点数多、 搜索范围大、效率低，但能得到最优解；当估价值h(n)大于当前点到目标节点的距离实际值时，搜索的点数少、搜索范围小、效率高，但不能保证得到最优解。为得到最优解，用欧几里得距离作为估价函数，即

(9)

在选好合适的代价函数并确定始发点和终止点之后，便可开始A*寻路过程。在栅格地图中利用8邻域节点扩展法的A*算法寻路过程可表述为：

1) 建立open列表和close列表，将起始方格放到open表中，初始化close列表为空。

2) 记当前节点为A，与该点相邻的8个方格为其子节点，将这些子节点放入open表中，同时将A节点移动到close表中(若A节点周围的8个点已在open表中且以A节点作为这8个点中任意一点的父节点减小了该点的F值，则更新该点)。

3) 将F值最小的节点放到close表中，并将该点作为当前节点A。

4) 重复步骤1)～步骤3)，直到把终点放到open表中。

5) 从当前点(终点)开始追溯父节点即为满足需求的路线。

根据以上步骤，采用A*算法对长为100 m的船舶进行寻路，最终结果见图6。由图6可知，船舶从起始点出发，能在障碍物威胁势场的影响下远离风机航行，并能在部分间隔较远的风机间穿行，最终到达目标位置。然而，即便在代价函数中已考虑转弯代价，采用A*算法得到的路径还是存在拐点较多的问题。这是由于在栅格环境中，8邻域搜索法限制路径只能朝8个方向延伸。为减少拐点，还需对该路径进行优化，使其更适合船舶在风电场区航行。

3 基于通视性检查的路径优化

对采用A*算法规划得到的路径进行通视性检查，不仅可减少路径拐点数量，还能缩短路径长度。[12]为减少运算量，这里只对路径点中的拐点做通视性检验。判断某点是否为拐点的依据是看其与相邻两点的连线是否共线。具体流程见图7。

将起始点P1作为当前节点,依次检查当前节点与拐点序列中的其他节点的通视性(即两点连线与障碍物之间的距离是否符合船舶航行安全距离要求)。若能通视,则保留该节点。最后将得到的拐点序列依次连线便得到优化之后的路径(见图8)。由图8可知，优化之后的路径总体走向不变，但拐点数量明显减少。

4 结束语

本文结合人工势场理论和A*算法，提出基于障碍物威胁势场的A*寻路算法。该算法可在保证船舶远离风机障碍的同时，以最短路径到达目标位置。相对于传统的*算法，采用本文提出的方法得到的路径不一定最短，但从船舶避障、操作复杂程度和最终路径长度等角度综合考虑是最优的。

本文提出的方法可为船舶在风电场区航行提供参考，但在威胁地图建模中未考虑风、浪、流等对船舶安全航行的影响。此外，基于通视性检查的关键点优化虽然能在一定程度上缩短路径长度，但各点间以线段连接得到的最终路线并不是符合条件的最短路线。

[1] 黄海威,邓开发. 改进的A*算法在游戏地图寻路中的应用[J]. 信息技术,2015(4):188-191.

[2] 方昕, 吕方兴. 一种改进A*算法的智能机器人路径规划[J]. 信息技术, 2015(9):40-42.

[3] 吴博, 文元桥, 吴贝,等. 水面无人艇避碰方法回顾与展望[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(3):456-461.

[4] 郭耕辰, 冯良炳, 邓亮,等. 基于A*算法与自适应分片的大规模最优路径规划[J]. 集成技术, 2014(2):68-77.

[5] 陈实, 刘纯武, 黄芝平,等. 基于稀疏A*算法的AUV全局路径规划[J]. 鱼雷技术, 2012, 20(4):271-275.

[6] JANET J A, LUO R C, KAY M G. The Essential Visibility Graph: An Approach to Global Motion Planning for Autonomous Mobile Robots[C]// IEEE International Conference on Robotics and Automation, 1995: 1958-1963.

[7] 单伟, 孟正大. 基于改进A*算法的平滑路径设计[J]. 东南大学学报(自然科学版), 2010(S1):155-161.

[8] 王红卫, 马勇, 谢勇,等. 基于平滑A*算法的移动机器人路径规划[J]. 同济大学学报(自然科学版), 2010, 38(11):1647-1650.

[9] 谢朔, 初秀民, 柳晨光,等. 船舶智能避碰研究综述及展望[J]. 交通信息与安全, 2016(1):1-9.

[10] 明力, 刘敬贤, 王先锋. 超大型船舶安全纵向间距计算模型[J]. 中国航海, 2014, 37(4):40-43.

[11] HART P E, NILSSON N J, RAPHAEL B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths[J]. IEEE Transactions on Systems Science & Cybernetics, 1972, 4(37):28-29.

[12] 陈彬, 李靖靖, 宋磊,等. 基于可视图和A*算法的连续模型路径搜索[J]. 交通信息与安全, 2012, 30(3):39-42.