基于改进人工势场法的维修分队机动路线规划方法*

豆超勇,古 平

(1.陆军工程大学石家庄校区,河北 石家庄 050003;2.中国人民解放军73087部队,江苏 徐州 221000)

装备维修保障分队是部队完成装备维修保障任务的主体,也是部队完成装备维修保障任务的中坚力量和具体操作者,地位与作用非常重要。科学合理地维修分队机动路线规划可以有效缩短机动时间,提升其维修效能,具有重要意义[1-2]。

路线规划问题一直都是人们研究的热点。目前运用比较多的方法有蚁群算法、遗传算法等,但其收敛速度相对较慢且规划路线相对较长,无法满足现代化战争对维修分队迅速、高效的机动路线的规划要求[3-4]。人工势场法具有对环境适应性强、鲁棒性好且计算简洁、快速的优点,在机动路线规划方面具有很广泛的应用前景。但传统人工势场法存在目标不可达和局部最小值等问题,使得该方法的应用受限[5-7]。本文在研究维修分队机动路线规划的时候对传统人工势场法进行了改进,解决了目标不可达和局部最小值的问题,对装备维修保障系统中装备维修保障分队的建模与仿真具有积极意义。

1 传统人工势场法

人工势场法(Artificial Potential Field, APF)是美国斯坦福大学的Khatib教授在1986年提出的一种用于解决机器人、无人机等智能体运动路线规划问题的虚拟力场方法。其基本思想是把智能体的运动环境抽象为目标点产生的引力势场和障碍物产生的斥力势场构成的势场空间,在这个空间中,智能体分别受到障碍物的斥力和目标点的引力,并在这两种力的共同作用下向目标点的方向运动,最终到达目标点位置[8]。

将人工势场法引入维修分队机动路线的规划模型,模拟维修分队在战场上受领维修任务后向维修地点机动的过程,具有鲁棒性良好、信息需求低、规划步骤简洁、运动轨迹平滑等优点,有助于装备维修保障系统的科学构建。

1.1 传统人工势场法的引力势场函数

假设维修地点坐标为pg=(xg,yg),那么维修分队机动到位置p=(x,y)时,引力势场函数可以用式(1)表示:

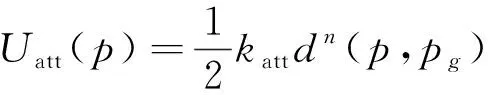
(1)

其中,katt为引力势场正比例系数,katt∈R+,适当增大katt可以增加维修地点引力势场的作用,在一定程度上减小出现极小值的概率;n为引力势场因子,其值大小是不固定的,并且取值的大小可以影响引力势场分布图的形状,本文取值n=2;d(p,pg)表示维修分队到维修地点的距离。所以,引力势场函数可以表示为

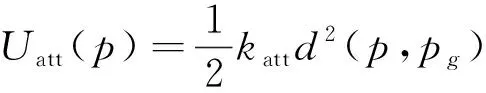
(2)

由于引力函数为引力势场函数的负梯度,所以引力函数可以表示为

Fatt(p)=-Uatt=-kattd(p,pg)

(3)

由式(3)可知,维修分队所受的引力大小与其到维修地点的距离成正比,距离越近引力越小,且可以通过调节引力势场正比例系数katt的大小来改变引力Fatt(p)的大小;维修分队所受的引力方向为维修分队指向维修地点。

1.2 传统人工势场法的斥力势场函数

假设障碍物坐标为po=(xo,yo),那么维修分队机动到位置p=(x,y)时,斥力势场函数可以用式(4)表示:

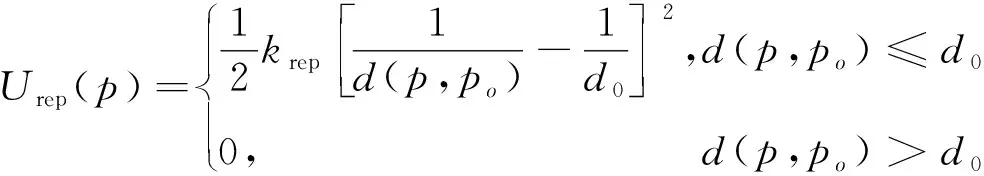
(4)

其中,krep为斥力势场正比例系数,krep∈R+,适当增大krep可以增加障碍物斥力势场的作用,使维修分队与障碍物保持更远的距离,从而确保机动路线更安全;d(p,po)表示维修分队与障碍物之间的距离;d0为受障碍物影响的最大距离,当且仅当维修分队机动到d0范围内的时候才会受到障碍物斥力作用。

由于斥力函数为斥力势场函数的负梯度,所以斥力函数可以表示为

(5)

由式(5)可知,维修分队所受的斥力大小与其到障碍物距离的平方成反比,距离越近斥力越大;当维修分队与障碍物距离d(p,po)趋向于d0时,维修分队所受的斥力Frep(p)也趋向于0;同样,也可以通过调节斥力势场正比例系数krep的大小来改变斥力Frep(p)的大小;维修分队所受的斥力方向为障碍物指向维修分队。

维修分队战场机动路线一般都要经过多个障碍物,产生的斥力势场也会有多个,所以其受到的斥力也应是多个斥力势场产生斥力的合力∑Frep(p)。那么,维修分队在机动过程中受到的引力与斥力的合力可以表示为

F(p)=Fatt(p)+∑Frep(p)

(6)

2 传统人工势场法的改进

在真实的作战环境内,维修分队的机动环境复杂多变,遇到障碍物的位置和数量也不确定,所以采用传统的人工势场法规划维修分队机动路线的时候就可能会出现目标不可达和局部极小值的问题,具体原因分析如下[9]:

1)随着维修分队不断向维修地点机动,其受到的引力会不断减小,而当维修地点附近出现斥力势场比较强的障碍物时,维修分队所受的斥力会因为与障碍物距离变小而增大,从而造成维修分队无法到达维修地点的现象。

2)在维修分队向维修地点机动的过程中,可能会存在某个位置,使得维修分队受到的维修地点引力和障碍物斥力大小相等、方向相反,从而出现维修分队到达该位置后来回震荡或者停止不动的现象,机动路线得到局部最优解。

针对上述两个问题,本文采用了优化斥力势场函数和类似BUG算法的方法来解决。

2.1 改进斥力势场函数

针对由引力变小和斥力变大引起的不能到达维修地点的问题,对斥力势场函数进行改进,具体如式(7)—(9)所示。

其中,m为调节因子,m∈R+。由斥力势场函数可得斥力函数为

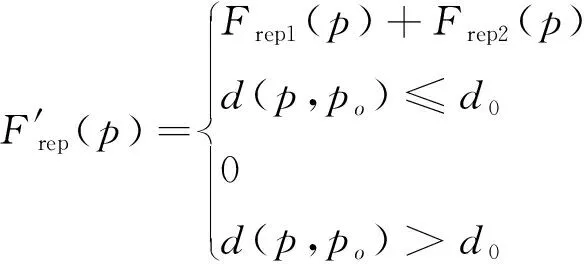
(7)

其中,

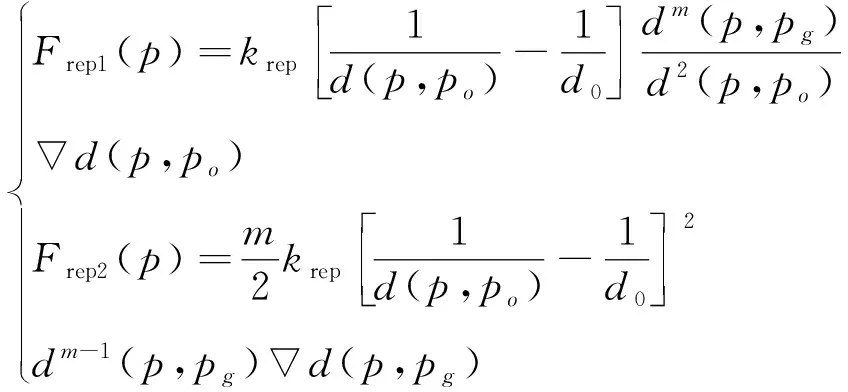
(8)

斥力Frep1(p)的方向为由障碍物指向维修分队;斥力Frep2(p)的方向与引力

(9)

Fatt(p)的方向一致,都为由维修分队指向维修地点,具体如图1所示。

图1 改进斥力函数受力示意图

将Frep2(p)与Frep1(p)相除,可得

(10)

为了便于观察其数值大小,设

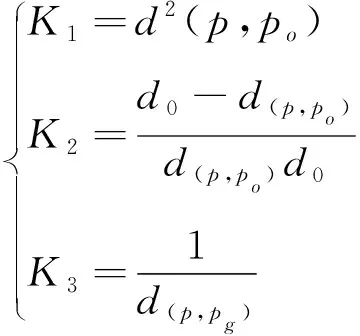
(11)

有

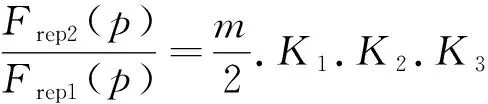
(12)

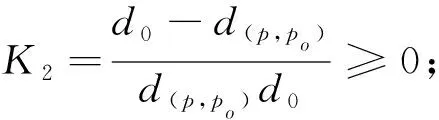
2.2 BUG-人工势场法

为使维修分队从局部最小值中逃离出来,采用了类似BUG算法，即在人工势场法路径规划的基础上增加应激反应,也就是BUG算法中的模拟昆虫沿障碍物爬行的行为[10]。当维修分队机动到局部极小值时,不再考虑维修地点对其产生的引力作用,而是沿着障碍物产生的斥力势场的等势线绕行,直到维修分队逃离局部极小值的区域。具体的算法流程如下所示。

Step1 通过位置传感器获取维修分队当前位置引力和斥力的大小和方向;

Step2 计算维修分队所受的合力,并判断其是否处于局部极小值,如果是,则执行步骤Step3;如果不是,则执行步骤Step5;

Step3 维修分队沿斥力势场等势线绕行机动,默认沿逆时针方向绕行;

Step4 判断维修分队是否已经逃离局部极小值区域,如果是,则结束绕行机动,执行步骤Step5;如果不是,则执行步骤Step3;

Step5 维修分队沿其所受合力的方向继续机动;

Step6 判断维修分队是否到达维修地点,如果是,则结束机动;如果不是,则执行步骤Step1。

其中,判断维修分队是否处于局部极小值可采用如下方法。

条件1:

F(p)=Fatt(p)+∑Frep(p)→0

(13)

条件2:|xj-xi|≪s

(14)

其中,条件1表示维修分队在位置p处受到的合力趋于0;条件2中|xj-xi|表示维修分队从i点机动到j点的直线距离,s则表示维修分队从i点机动到j点的机动路程,那么,条件2则表示维修分队在机动了很长路程后位移却很小。所以,如果符合条件1或者条件2时,就认为维修分队处于局部极小值。

3 仿真结果与分析

为了验证改进算法的先进性和合理性,给出仿真案例如下。

设装备维修保障分队在原点(0,0)位置接收到上级任务,命令其机动至维修地点进行维修作业。

1)根据传统人工势场法设定斥力势场函数,在如图2所示障碍物位置情况下通过不断仿真找出满足目标不可达情形的维修地点位置(4750,5380)。

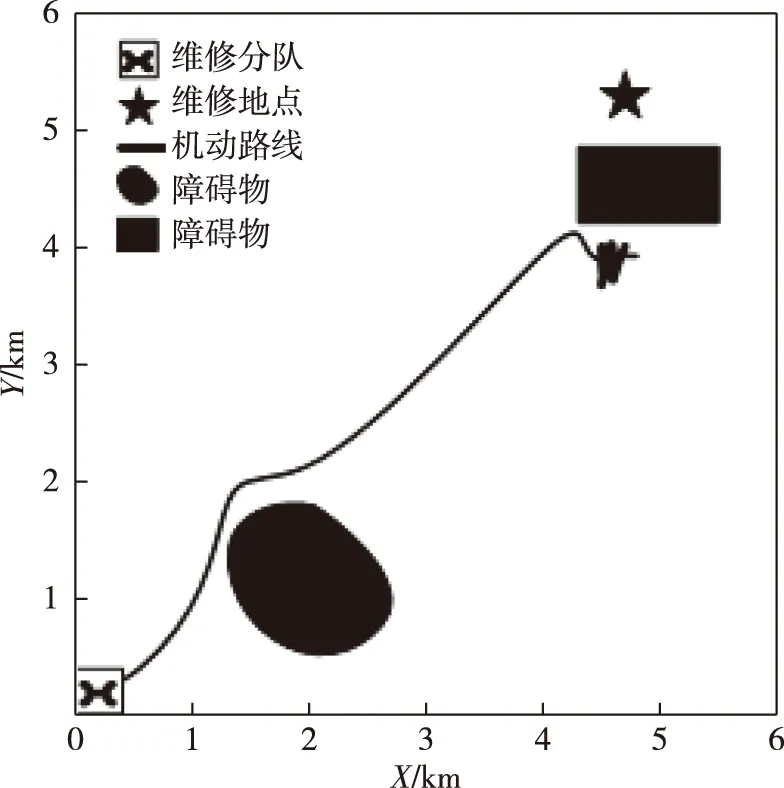
图2 传统人工势场法规划路线一

由图2可以看出,在维修分队向维修地点机动的过程中,其受到的引力会不断减小,而当维修地点附近出现斥力势场比较强的障碍物时,维修分队所受的斥力会因为与障碍物距离变小而增大,从而造成维修分队无法到达维修地点的现象。

2)根据改进人工势场法设定斥力势场函数,并设定与图2所示障碍物和维修地点位置相同的仿真条件进行仿真,得出图3。

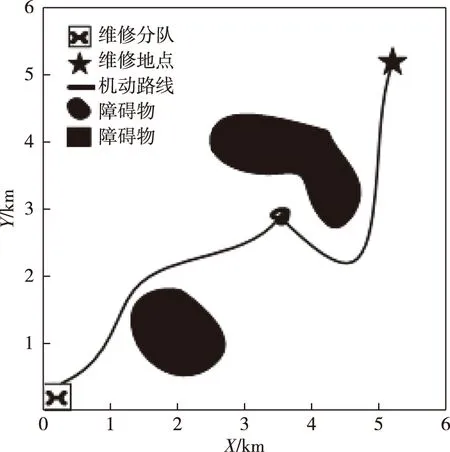
图3 改进人工势场法规划路线一

由图3可以看出,在维修分队向维修地点机动的过程中,改进后的斥力势场函数中,斥力随着维修分队不断向维修地点靠近而变小,维修分队所受合力的方向也一直都指向维修地点或其附近,并最终顺利到达维修地点。

3)根据传统人工势场法设定势场函数,在如图3所示障碍物位置情况下通过不断仿真找出满足局部最小值情形的维修地点位置(5380,5380),如图4。

图4 传统人工势场法规划路线二

由图4可以看出,在维修分队向维修地点机动的过程中,存在某个位置,使得维修分队受到的维修地点引力和障碍物斥力大小相等、方向相反,从而使维修分队到达该位置后来回震荡或者停止不动的现象,机动路线得到局部最优解。

4)根据改进人工势场法设定势场函数和增加BUG算法的应激反应,并设定与图4所示障碍物和维修地点位置相同的仿真条件进行仿真,得出图5。

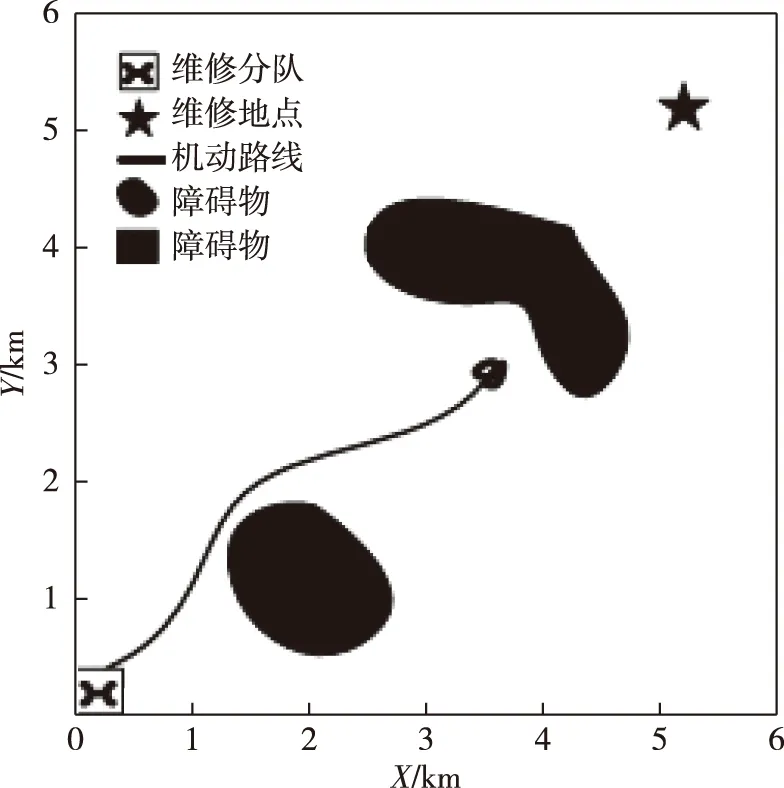
图5 改进人工势场法规划路线二

由图5可以看出,在维修分队向维修地点机动的过程中,改进人工势场法在维修分队出现局部极小值的情况时,模拟BUG算法中沿障碍物爬行的行为沿着障碍物产生的斥力势场的等势线逆时针绕行,直到维修分队逃离局部极小值的区域,然后继续在所受合力的影响下继续机动,并最终顺利到达维修地点。

4 结束语

本文对人工势场法在装备维修保障系统维修分队机动路线规划建模与仿真中的应用进行了尝试,并针对传统人工势场法的不足进行了改进,通过仿真实验验证了改进人工势场法的可行性,对人工势场法在装备维修保障系统建模与仿真领域的拓展应用起到了一定作用。