双向通航港口船舶调度优化模型与算法
张新宇, 李瑞杰, 林 俊, 陈 向
(1. 大连海事大学 航海动态仿真与控制交通行业重点实验室, 辽宁 大连 116026; 2. 龙岩学院 机电工程学院, 福建 龙岩 364012)
海上运输是国际贸易中最主要的货物运输方式,近年来国内外各港口为适应不断拥挤的海上交通,或扩大建设规模,或不断拓宽航道,从单向航道逐步发展到双向航道,甚至是复式航道。双向航道在减少船舶在港待航时间、提高航道利用率和缓解通航压力等方面相对单向航道有很大优势。在港口实际操作中,双向通航港口船舶进出航道需考虑众多因素,涉及多个部门之间的协调,目前缺少一个协调高效的优化调度方法。同时,针对双向通航港口船舶调度优化的研究相对很少,相关研究主要有双向通航安全、港口船舶调度优化建模和调度模型求解算法等。
在双向通航安全方面:GAAFARY等[1]从船舶操纵控制方面分析土耳其海峡双向通航的可行性;OZGECAN等[2]对航行条件复杂且交通拥挤的伊斯坦布尔海峡的船舶交通进行风险分析:OZGECAN等[3]研究一种关于船舶进出伊斯坦布尔海峡顺序的调度算法。这些研究大多针对海峡或船闸的通航安全,并不完全适于解决一般双向通航港口的船舶调度问题。
港口船舶调度模型主要用来提高船舶通过港区可航水域的效率和码头资源调度效率。FILIPOWIC[4]将受限水域抽象为包括多个节点的图形结构,利用种群学习算法实现过往船舶对不同节点的选择来平衡或缓解局部航段的拥挤,达到均衡交通流的效果;徐国裕等[5]在船舶调度中引入优先级,用船舶种类、吨位、吃水、装载状况和泊位距离等参数推定综合权重,应用工作排序理论建立单向水道船舶进出港最佳排序模式;王金涛[6]利用容量转换和协同决策思想建立多目标船舶调度模型,对单向航道船舶调度问题进行优化。这些提高航道使用效率的调度模型或基于受限水域、交汇水域,或基于单向航道,并不适用于双向通航港口的船舶调度。在码头资源调度优化方面,IMAI等[7-8]针对泊位优先权、连续泊位等泊位分配问题开展一系列研究。尽管船舶调度优化模型方面的研究成果较多,但主要针对的是泊位和岸桥等码头资源的调度,而港口船舶作业是一个连续的过程,满足码头作业效率最大化可能导致船舶进出航道顺序不合理,降低船舶整体的调度效率。为此,ZHANG等[9]对单向航道和泊位资源协调调度进行优化建模,结果表明协调航道和泊位等港口资源形成统一的船舶调度方案,确实能提高船舶调度效率。
因此,本文在对多个港口进行调研的基础上,分析港口双向通航船舶调度需求,建立双向通航港口船舶调度优化多目标数学模型,设计多目标遗传算法获取最佳调度方案。
1 问题描述
航道实施双向通航是有条件的,双向通航港口船舶调度必须考虑单向通航与双向通航的转换问题。船舶在港作业是一个连续的过程,一个安全可行的船舶调度方案应能提前预知并避免船舶在航道上面临紧迫形势或进港之后没有泊位停靠的问题。双向通航港口船舶调度的关键在于确定船舶通航模式(单向/双向)、协调各港口资源、合理安排船舶进出航道的顺序和时间,在保证安全的情况下使尽可能多的船舶尽快进出港,提高船舶进出港效率。
2 模型建立
2.1 模型假设
影响港口船舶调度的因素多且复杂,本文提取关键因素,作以下假设。
1) 针对某时间段内出现的船舶调度问题进行建模。
2) 港口有多个锚地且容量无限。
3) 进港船舶在锚地等候进港,出港船舶在泊位等候出港(基于此,进港船舶的航行距离为锚地到泊位的距离,出港船舶的航行距离为泊位到航道起点的距离)。
4) 航道水深满足船舶进出港要求。
5) 船舶申请进出港时刻,引航员、拖船和泊位等已分配好并准备就绪。
6) 采用双向通航港口规则,其中对单向通航和双向通航的规定为:除下列情况只允许单向通航外,其它均为双向通航。
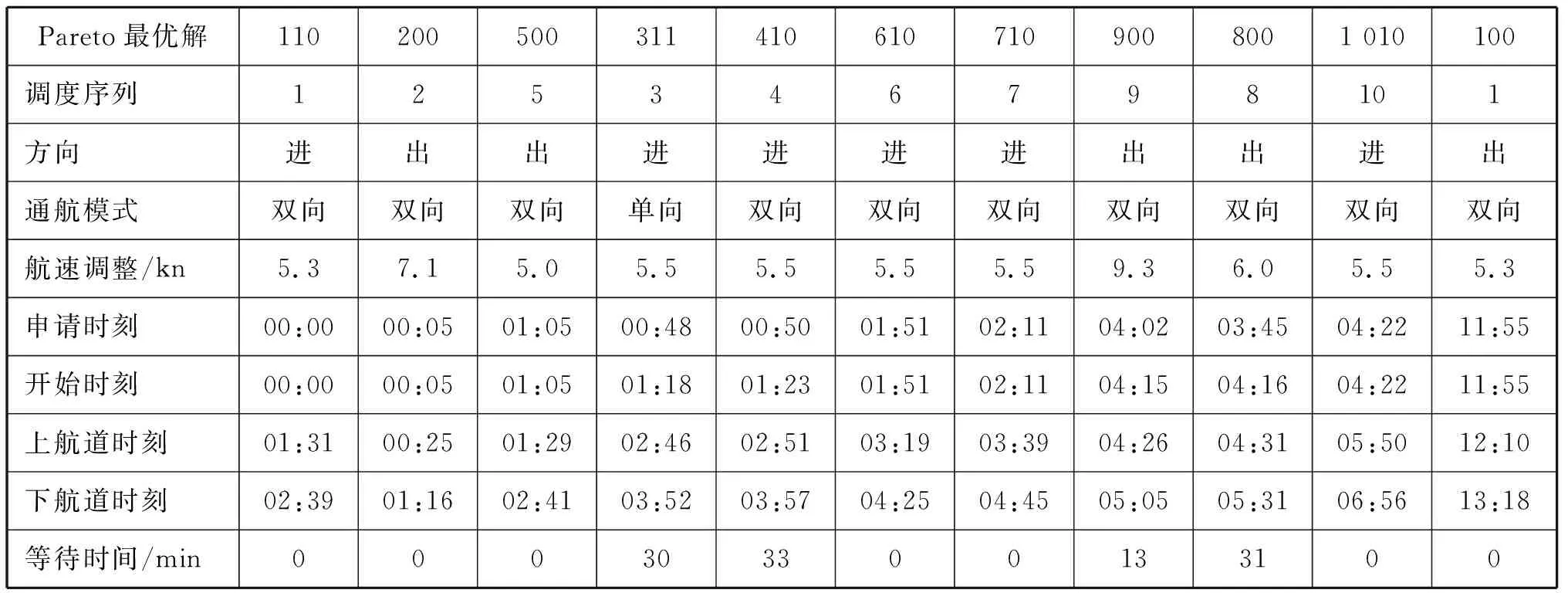
(1) 视程 (2) 风力≥W1; (3) 单船船宽≥Y1; (5) 拟相对航行的两船船宽之和≥Y2。 经调研发现,由于港口船舶调度涉及众多部门,对调度结果的期望各不相同。在形成统一的船舶调度方案时,从整体上看,总调度时间和总等待时间越短,表明调度效率越高。因此,从高效性出发,建立总调度时间最少和总等待时间最少的目标函数。 minT1=max(fi)-[Ijmin(t1j)+ (1) (2) 式(1)和式(2)中:总调度时间T1是最迟完成调度时刻与最早开始调度时刻的差值;总等待时间T2包括所有进港船舶在锚地等待进港时间和出港船舶在泊位等待出港时间。前者为开始进港时刻与申请进港时刻之差;后者为开始出港时刻与申请出港时刻之差。 2.3.1模式转换约束 由于双向通航是有条件的,不可避免地会出现单向通航的情况,因此模式转换约束是双向通航港口船舶调度的必然要求。根据假设中的通航规则,建立单向/双向通航模式转换约束为 (3) 2.3.2连续性约束 船舶在港作业是一个连续的过程,一旦开始调度时刻确定,在船舶航速、船舶当前位置、船舶到达航道和泊位的距离已知的情况下,船舶到达航道、泊位的时刻即可确定。 2.3.2.1 开始时刻约束 式(4)为船舶i开始进港时刻不得早于其申请进港时刻,且船舶i进港时,其所停靠的泊位必须是空闲的,否则船舶i必须在锚地等待。式(5)为船舶i开始出港时刻不得早于其申请出港时刻。 2.3.2.2 航行时刻约束 通常情况下,船舶到达航道起点、航道终点、靠泊和离泊时须向交通管理中心(Vessel Traffic Service, VTS)报告。在建模时,选择航道起点、航道终点和泊位等作为关键点,主要计算船舶上航道时刻、下航道时刻、到达泊位时刻、靠好泊位时刻和完成调度时刻等。计算方法分别为 (12) 2.3.3安全性约束 2.3.3.1 任意2艘船舶之间的安全约束 为保证船舶在航道中安全航行,任意2艘船舶之间必须保持一定的安全间距,包括纵向安全间距和横向安全间距。纵向安全间距根据船舶航向的异同分为异向安全间距和同向安全间距。[10]通过从空间到时间的转换,将安全间距转换为安全时间间隔,在连续性约束的基础上调整船舶调度开始时刻,以避免形成紧迫形势。从空间到时间转换主要考虑单向/双向通航模式、船舶进出港方向、相遇位置和泊位远近。 2.3.3.2 不同通航模式转换下的安全约束 单向通航涉及同向安全间距和异向安全间距,双向通航涉及同向安全间距和横向安全间距。 双向通航港口船舶调度多目标遗传算法流程见图1。 由于港口船舶调度的实际情况十分复杂,采用模拟数据验证模型的合理性和算法的有效性。在对多个港口进行调研的基础上,模拟港口数据建立船舶调度基础数据库,模拟港口的航道条件、到港船舶等情况进行调度试验。 调度基础数据库中建立4个锚地的信息、34个泊位的信息和50艘船舶的基本信息。 为对调度方案进行可行性验证,设置调度试验的参数如下。 1) 港口参数:航速最低5 kn,最高10 kn;船舶数量10艘;V=5 000,W=6;调度期间为0:00—12:00,E=2,C=6;g0=5,g1=5。 2) 遗传算法参数:种群大小为200代,父代与子代之间的代沟为0.9,交叉概率为0.9,变异概率为0.05,终止代数为200代。 图2为港口船舶调度试验结果。由图2可知,有3个Pareto最优解,其中,最小总调度时间为733 min,最小总等待时间为107 min,平均每艘船舶的等待时间约为10 min。由种群均值的变化可知,种群在不断地寻找最优解;由种群进化图可知,第一目标值在20代左右收敛,第二目标值在60代左右收敛。这说明双向通航港口船舶调度多目标遗传算法能有效搜索双向通航情况下船舶进出航道的调度方案。 表2按照调度时间先后的序列给出Pareto1解的详细调度方案。 1) 一般安全性检验:航速调整是针对同向先后航行的船舶调整其航速,避免船舶在航道上追越,如编号为4的船舶紧随编号为3的船舶进港上航道,编号为4的船舶的航速不应超过编号为3的船舶的航速,航速由7.7 kn调整为5.5 kn。只有船舶申请进出港之后才可对其进行调度,如按照同向安全时间间隔的约束,编号为5的出港船舶在编号为2的船舶上航道之后的一个同向安全时间间隔之后(00:30)即可上航道,但由于编号为5的船舶此时尚未申请调度,因此不能安排其出港,直到其申请出港时(01:05)方可安排出港。 2) 双向通航安全性检验:双向通航进港船舶与双向通航出港船舶之间只需在航道上保持规定横向安全距离即可,彼此上航道时刻不受约束,如编号为1的进港船舶在01:31时刻上航道(航道起点处),编号为2的出港船舶可在00:25时刻上航道(航道终点处)。但是,同是双向通航进港或双向通航出港的船舶,先后2艘船舶上航道时刻之间至少保持1个同向安全时间间隔,如编号为2及5的双向通航出港船舶和编号为4及6的双向通航进港船舶均满足要求。 3) 双向通航与单向通航转换的安全性检验:当调度中出现单向通航的船舶时,不允许反向的单向通航船舶或双向通航船舶进出航道,但允许同向的单向通航船舶或双向通航船舶进出航道,且同向航行的船舶上航道时刻之间至少保持1个同向安全时间间隔,既保证安全又提高调度效率。如编号为3的单向通航船舶进港时,在上航道至下航道期间(02:46—03:52)均没有单向通航出港船舶或双向通航出港船舶,但编号为4的双向通航进港船舶可紧随其后,相应地上航道时刻之间保持1个同向安全时间间隔(5 min)。 表2 Pareto最优解调度优化方案 以上分析表明,所研究的调度方案具有可行性,双向通航港口船舶调度多目标遗传算法能有效求解双向通航港口船舶调度优化模型,求解结果满足模型中的目标要求和约束条件,并在保证船舶安全航行的情况下有效提高其进出港效率,从而验证模型的合理性和算法的有效性。需指出,在实际操作中,港口调度部门可根据实际需求选择相应的Pareto最优解。例如,若要求总调度时间最短,则可选择Pareto3解作为调度方案。 本文研究双向通航港口船舶调度问题,建立以总调度时间和总等待时间最少为目标,以单向/双向通航转换、连续性和安全性为约束的双向通航港口船舶调度优化数学模型。针对双向通航船舶调度问题多约束、多目标和大规模的特点,设计双向通航港口船舶调度多目标遗传算法,搜索船舶进出航道的最佳调度方案。试验结果表明,本文提出的双向通航港口船舶调度优化方法具有合理性和可行性,符合港口船舶调度规律,且能在保证船舶安全航行的前提下有效提高港口船舶调度效率。但是,本文所建模型相对简单,需进一步加以完善。此外,如何在电子海图上进行调度试验来验证本文所提出优化方法的可行性也是今后研究的方向。 [1] GAAFARY M M, MOLESH M. Ship Hydrodynamics and Optimal Control During Two-Way Traffic - A Proposed System of Navigation in Suez Canal [J]. Ocean Engineering and Coastal Resources, 2008,1:37-45. [2] ULUSCU O S, OZBAS B, ALTIOK T, et al. Risk Analysis of the Vessel Traffic in the Strait of Istanbul[J].Risk Analysis, 2009,29(10):1454-1472. [3] ULUSCU O S, OZGECAN S. Transit Vessel Scheduling in the Strait of Istanbul[J]. Journal of Navigation, 2009,62(1):59-77. [4] FILIPOWIC W. Vessel Traffic Control Problems [J]. Journal of Navigation, 2004,57(1):15-24. [5] 徐国裕,郭涂城,吴兆麟.单线水道船舶进出港最佳排序模式[J].大连海事大学学报, 2008,34(4):150-153. [6] 王金涛.基于单向航道的船舶调度优化模型与算法研究[D].大连:大连海事大学, 2014. [7] IMAI A, NISHIMURA E, PAPADIMITRIOU S. Berth Allocation with Service Priority [J]. Transportation Research Part B, 2003,37(5):437-457. [8] IMAI A, SUN X, NISHIMURA E, et al. Berth Allocation in a Container Port: Using a Continuous Location Space Approach [J]. Transportation Research Part B, 2005,39:199-221. [9] ZHANG Xinyu, LIN Jun, GUO Zijian, et al. Vessel Transportation Scheduling Optimization Based on Channel-Berth Coordination [J]. Ocean Engineering, 2016,112:145-152. [10] LIN Jun, ZHANG Xinyu, YIN Yong, et al. Optimization of Ship Scheduling Based on One-Way Fairway [J]. Lecture Notes in Computer Science,2014:479-486.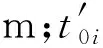
2.2 目标函数
2.3 约束条件
3 算法设计
4 模型与算法验证
4.1 基础数据
4.2 调度试验
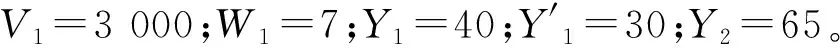
5 结束语

