p-调和方程在次线性增长下的Liouville定理*

王新敬

(西北工业大学 应用数学系,西安 710129)

调和方程的Liouville定理是经典的结果.经典的Liouville定理是说当调和函数有界时,那么就有函数是常数.在各种条件下研究偏微分方程的Liouville定理是人们关注的热点问题.文献[1]给出了具有非负Ricci曲率的Rieman流形上的非负调和方程的解是常数.文献[2]中作了进一步推广,得到流形上次线性增长的调和方程的解也是常数.文献[3]得到了有界的p-调和方程的Liouville定理.

文中研究p-调和方程的弱解的Liouville定理.受到文献[2]的启发并借助文献[3]中的证明思想,建立n中p-调和方程

-Δpu∶=-div(|u|p-2u)=0

(1)

的弱解在满足次线性增长时的Liouville定理.

1 记号和准备知识

用Br(x)⊆n表示以x为中心,r>0为半径的球.注意到式(1)是散度型椭圆方程.现给出式(1)的弱解的定义.

下面给出要用到的不等式[4-5]:

‖f‖Lq(Ω)≤C‖f‖Wk,p(Ω),

关于文中用的更多的Sobolev空间的知识可参见文献[4-6]等.

2 主要结果和证明

为证明式(1)的Liouville定理,先给出要用到的两个引理.

证明: 关于指标k作迭代

并注意到

则立即得到

引理2 若u为p-调和方程(1)的弱解,则对所有的λ≥0,R>0和σ>0,存在正常数C使得

特别地,对所有的k,n∈N,有

证明: 取BR(0)相对于BR+σ(0)的截断函数ξ满足0≤ξ≤1,ξ在BR(0)上取值为1,在BR+σ(0)外取值为零,且|

对(1)关于xk微分，再乘以|uk|λukξ2,然后在区域上积分,利用分部积分后得到

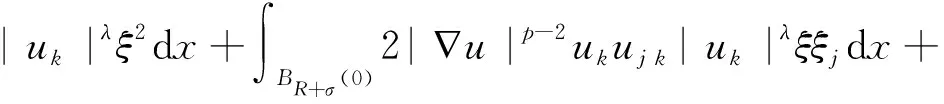
|uk|λukujξξjdx,这里j=1,…,n.

关于指标k求和,利用p>1和Hölder不等式,可得到

(2)

将式(2)移项,有

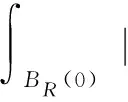
易得

特别地,取合适的λ,即λ=pkn-1-p,对所有的k,n∈N,有

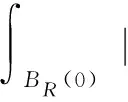
文中的主要结果是

定理1 假设u为满足(1)的弱解,且u满足次线性增长条件

则u为常数,其中r(x)是x到原点的距离.

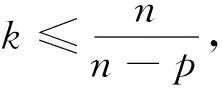
选取w=|代入,利用引理2,得到

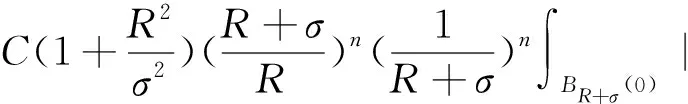
(3)

由式(3),利用引理1,得到

(4)

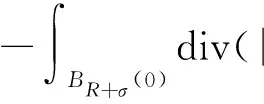
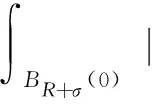
其中ξ为引理2中给出的截断函数.利用Hölder不等式,

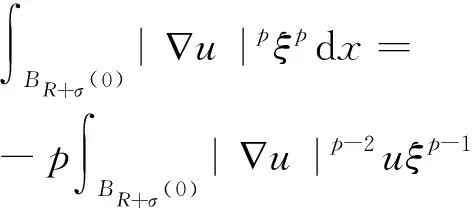
(5)

由式(4)和式(5)可得

(6)

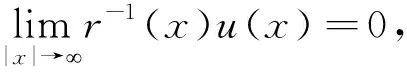
3 结 论

文中利用迭代技巧建立了全空间上p-调和方程的弱解在满足次线性增长时的Liouville型定理,其结果是对于经典的Liouville定理的推广,把原来经典的解的条件是有界性减弱建立为次线性增长,这对于具有同样类型条件的问题具有一定的指导意义.

参考文献：

[1] YAU S.Harmonic Functions on Complete Riemannian Manifolds[J].Communications on Pure and Applied Mathematics,1975(27):201.

[2] CHENG S.Liouville Theorem for Harmonic Maps[J].Proceedings of Symposia in Pure Mathematics,1980(36):147.

[3] BIRINDELLI I,DEMENGEL F.Some Liouville Theorems for thep-Laplacian[J].Electronic Journal of Differential Equations,2002(8):35.

[4] EVANS L.Partial Differential Equations[M].Washington D.C.:American Mathematical Society,1998.

[5] GILBARG D,TRUDINGER N.Elliptic Partial Differential Equations of Second Order[M].Berlin:Springer-Verlage,1983.

[6] LI P.Geometric Analysis[M].Cambridge: Cambridge University Press,2012.

[7] TOLKSDORFF P.Regularity for a More General Class of Quasilinear Elliptic Equations[J].Journal of Differential Equations,1984(51):126.