椭偏法光学材料折射率测量精度分析*

武月月，弥 谦

(西安工业大学 光电工程学院,西安 710021)

椭偏法是一种先进的测量薄膜参数的方法,在科研上应用范围非常广[1-2].许多研究者对椭偏法测量光学参数的影响因素方面进行了研究.现阶段测折射率不仅有椭偏法还有V棱镜法[3-4]、最小偏向角法[3-5]和迈克尔逊干涉法[6]等方法,这些方法对待测样品的表面加工要求比较高,大量的光学材料制造会在测定材料性能的时间和效率上带来很多麻烦.前期的研究者在椭偏法测量折射率大部分倾向于单一波长和多角度入射,所以侧角误差大.文献[7]用椭偏法测量了入射光波长0.632 μm,入射角50°～85°时某合金钢的光学常数.结果表明:用椭偏法测量合金钢光学常数时采用较小入射角能获得更精确的样品光学常数.文献[8]采用WJZ-II型椭偏仪,入射光波长为635 nm测量,入射角为70°测量光学材料,对实验进行改进,将光接收器的光电探头前面放置一个2 mm的小孔光阑和加工了一个一维可调位移平台,可调平台为60 mm×60 mm的钢结构体,折射率测量精度达到1×10-3.文献[9]用高效光学实验室的常规仪器完成椭偏法测量薄膜厚度与折射率.对实验测量时的若干问题进行讨论,对材料测量时入射角为70°,折射率测量精度达到1×10-3.

基于实现高精度测量光学材料折射率的原因,文中采用椭偏法测光学材料的折射率,对实验仪器的选取和实验过程进行设计,得出实验数据;对实验中的光强强度变化误差、入射角精度以及起偏器与检偏器转动误差等方面进行误差分析,实现低成本高精度测量光学材料参数.

1 测量原理与装置

使用椭偏法测量光学材料折射率的原理如下:一束波长λ的入射光,通过起偏器,得到一束电场矢量的线偏光,入射到待测样品表面,i0为入射角,入射光经过待测样品变成线偏振光[10],n0、n为环境和材料的折射率,i1为折射角.根据椭圆偏振光与折射率的关系求出光学材料的折射率.

根据偏振光[11]原理,对待测样品表面反射和折射进行分析,图1是光在样品界面上的反射与折射示意图[12].

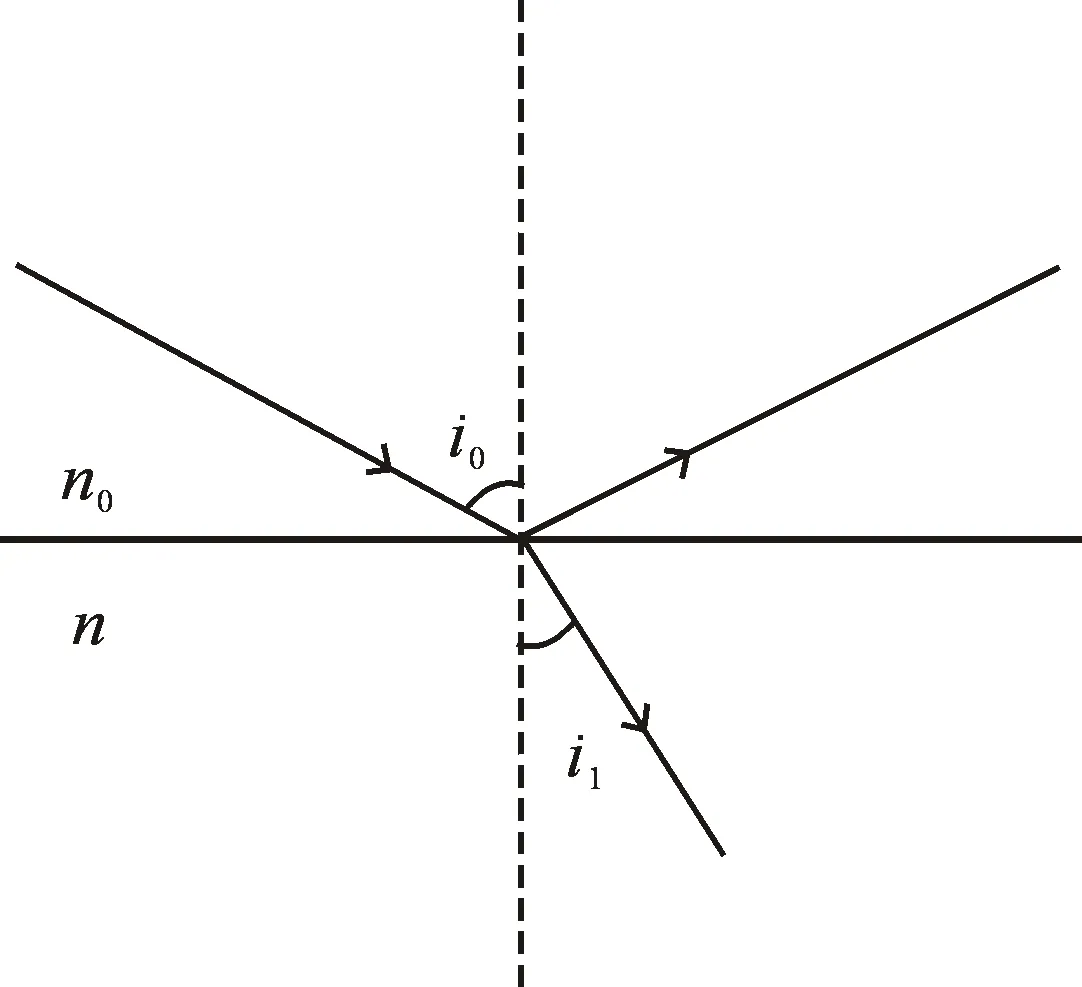
图1 样品表面光路图

在光学材料界面发生反射与折射,光束通过被测样品,在其表面发生反射和折射,rp为p方向上的反射系数;rs为s方向上的反射系数.根据菲涅尔公式[13]得

(1)

则两个方向的反射系数之比ρ可表示为

(2)

式中:Ψ为检偏角;Δ为p分量和s分量相移之差.在椭偏法中称为椭偏参数.椭偏参数利用椭偏法直接测量得出.

根据反射系数ρ与折射定律n0sini0=nsini1,可得折射率n为

(3)

式(3)表示待测样品折射率与偏振角Ψ和入射角i0的关系,在实验测量时固定入射角的角度,通过测量偏振角进而计算出光学材料折射率.

基于椭偏法原理,用计算机模拟偏振角的精度与入射角的关系,材料的折射率n取1.6～1.9和2.4～2.7范围之间,折射率以0.000 1幅度变化,分别选取10°～80°之间的角度入射,图2为偏振角的精度随入射角的变化图.

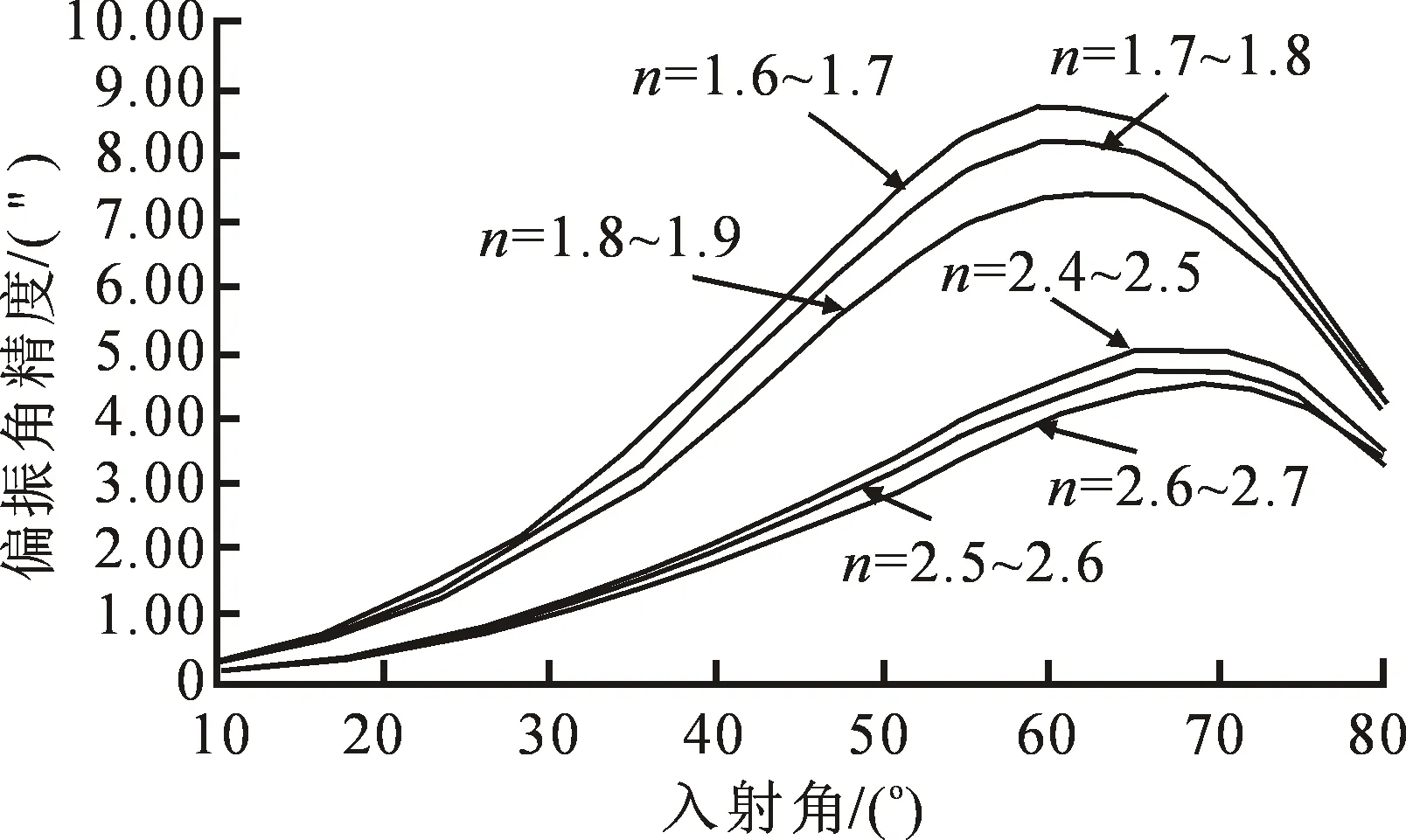
图2 偏振角的精度随入射角的变化图

基于以上的模拟验证,得出结果如下:在实验测量时,折射率在1.6～1.9之间,选取60°作为固定入射角;折射率在2.4～2.7之间,选取70°作为固定入射角,此时偏振角变化幅度大,灵敏度高.

实验框架图如图3所示.光源经准直扩束成一束准直光源,光源经过起偏器岀射一束线偏光,线偏光以一定的入射角经过待测样品反射出一束偏振光,检偏器检测偏振光,探测器接收光强的变化,转动检偏器,当发光强度为零时,记录此时检偏器上透光方向转动的角度.对一个点进行多次读取,多次测量,对测量结果进行误差分析,包括系统误差和偶然误差,分析此时折射率误差精度.本实验系统光源选取He-Ne激光,波长为632.8 nm,光束的相干性和方向性强;起偏器、检偏器选用格兰棱镜,与其他偏光板相比,其透过率和偏光纯度更高;选取SC103型步进电机,其驱动器细分数设置为64,旋转台的转角为0.009 °;被测材料选用平面K9玻璃;选取DH-JG2型光电探测器.

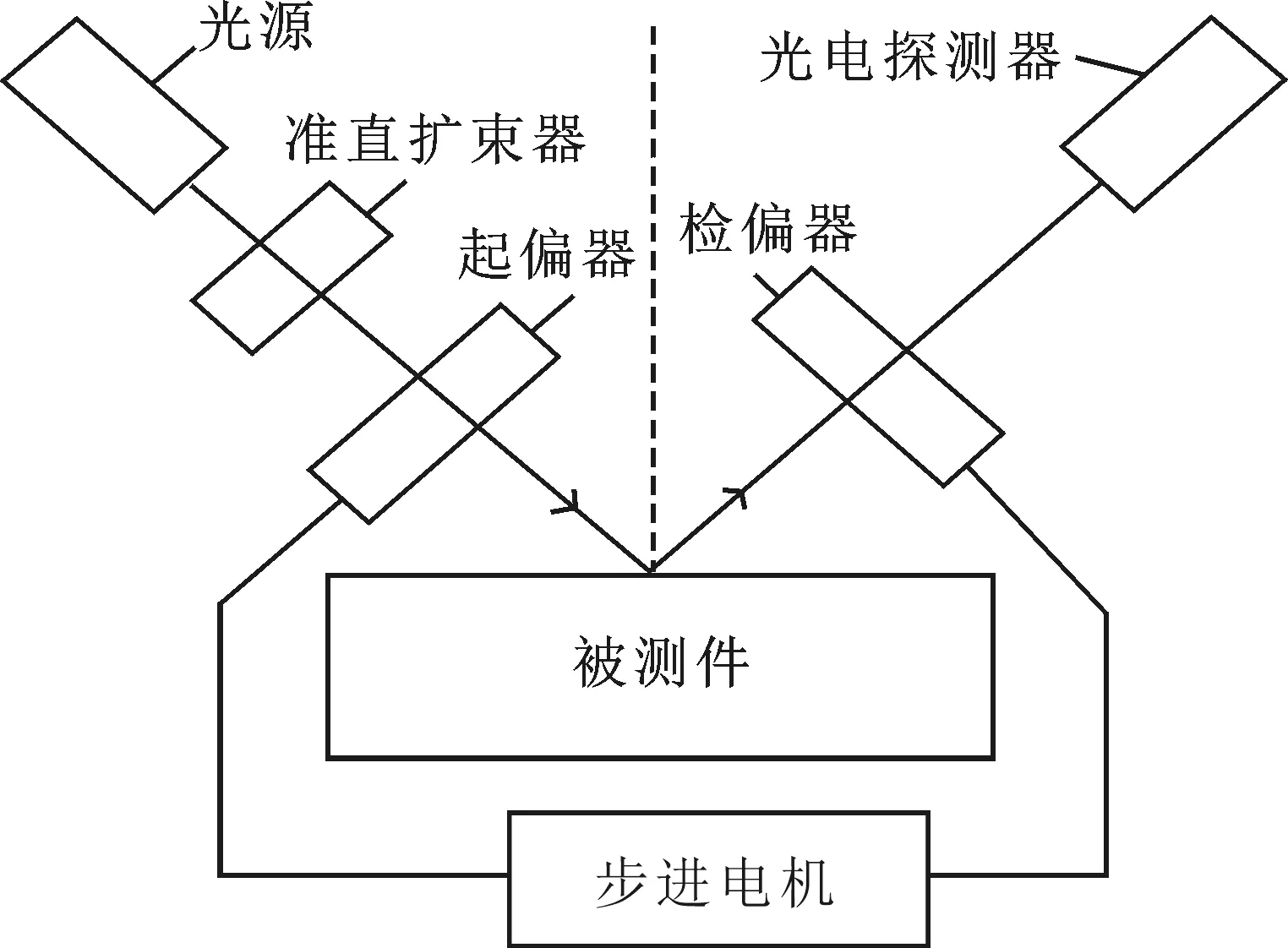
图3 实验系统框架图

2 测量结果与分析

2.1 材料折射率测量

以平行于平板玻璃表面的方向为x轴,垂直于平板玻璃表面的方向为y轴,建立直角坐标系.通过步进电机调整起偏器偏振方向,使入射到待测表面的光束是一束s光与p光夹角为45°的线偏光;线偏光以60°入射经待测样品反射,由于s光与p光的反射率不同,所以只会影响反射光的偏振方向,出射光仍为线偏光.

使用步进电机控制器控制电动转台进行精密转动检偏器.探测器接收到光信号强度,记录发光强度变化时对应此时的检偏角大小,当检偏器的偏振方向与反射光振动方向垂直时,发光强度为零.当发光强度为零时,确定检偏器的位置,测量此时的检偏角.

波长为632.8 nm时,通过对这些数据进行拟合,得到检偏角与发光强度的拟合曲线图,如图4所示,从图4中可以看出检偏角与发光强度成正弦曲线分布,拟合曲线图中看出检偏角与发光强度存在一定的正弦关系.进行多次测量,对多次测量结果进行均方根误差计算.测量发光强度为零时所对应的检偏角、材料折射率和折射率误差Δn见表1,表1仅列举了均方根误差较小的两次测量结果.材料折射率三次测量的均方根误差依次为3.67×10-4、9.16×10-4和2.08×10-4,比较多次测量结果得出折射率测量误差为9.16×10-4.

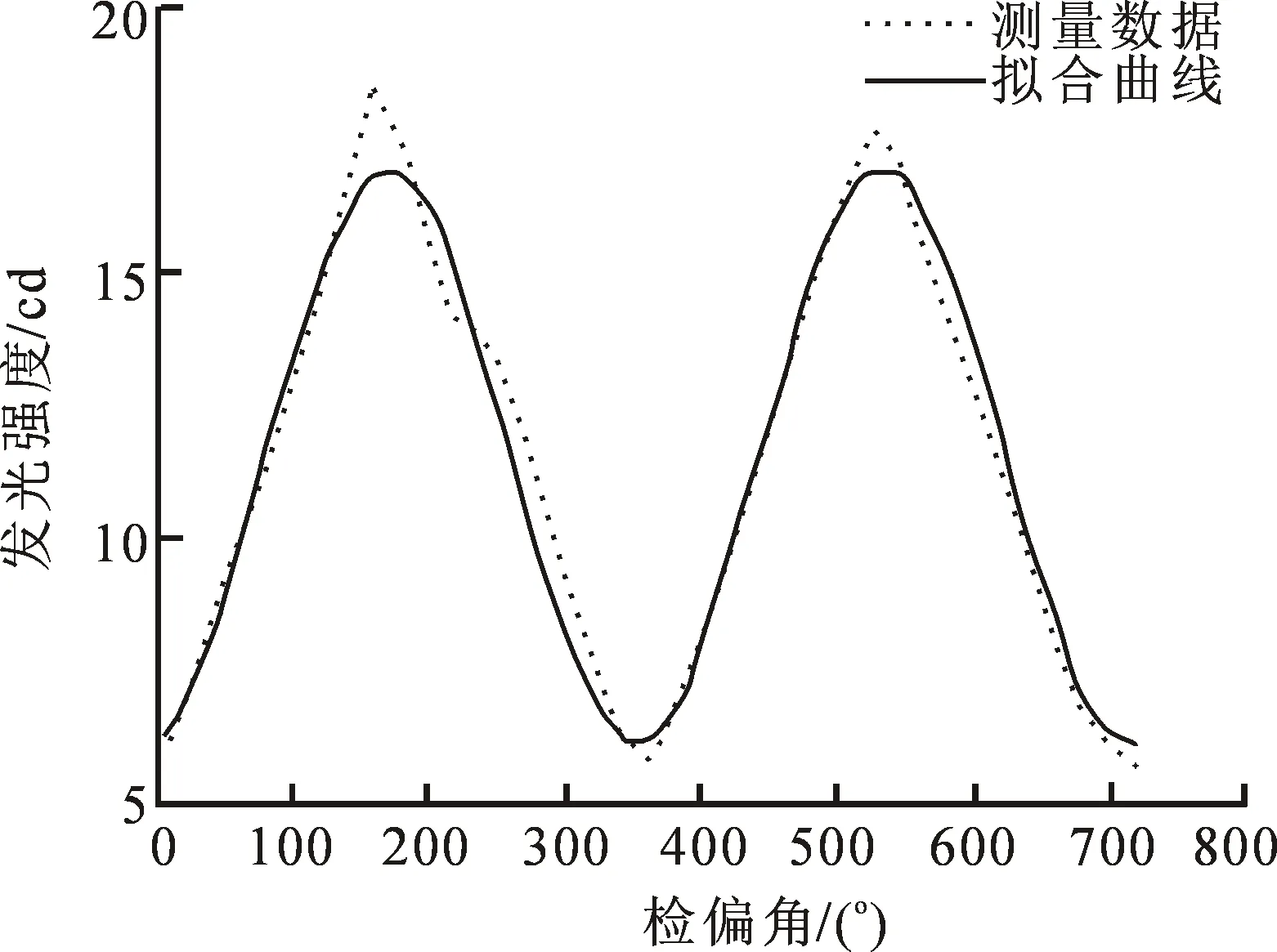
图4 检偏角与发光强度拟合曲线图

2.2 测量误差分析

为了证明此种方法的准确度,根据式(3)中特定波长下的折射率,对椭偏角进行反推.反推结果与实验测量的线偏角的均方根误差为16″.可以看出,实验测量的结果与本文提到的方法反推结果一致.对测量精度高的原因做了如下分析.

发光强度的变化会影响检偏角的测量,但是在测量时,选取的点是消光位置处的检偏角,消光位置处发光强度为零,一般情况下,强度变化不大,所以在消光点处发光强度变化不考虑.

玻璃空间角度[14]的变化会影响入射角的误差,由于在微调玻璃角度时,对角度误差进行测量,验证与所定基准线是否存在着微小的误差.把玻璃材料按实验装置固定后,用激光笔垂直照射到玻璃材料,反射光在墙上,找基准点,测量基准点到待测材料距离和基准点到反射点的距离,对反射光的微小角度计算,所测的左右偏转的角度为0.048°，影响入射角的法线位置,进而影响入射角大小,标准入射角为60°时,折射率误差为±4.008 1×10-4,考虑玻璃空间角度偏差,折射率误差为±2.644 6×10-4,通过对比,两者的折射率误差为±1.363 5×10-4，得出玻璃空间角度偏差影响折射率的误差比较大,实际的入射角为59.952°.

采用PRS103精密旋转台对待测材料的入射角进行调节,驱动方式为微分头,读数方式为游标读数.其测角精度达到10″,最小刻度为1°,最小读数为5′.入射角为60°时,折射率误差为±4.008 1×10-4,考虑精密旋转台误差时,折射率误差为±3.922 8×10-4,两者的折射率误差为±0.085 3×10-4.

从以上分析得出，玻璃空间角度和旋转台转角会影响入射角的变化,由于旋转台定位误差可以通过实验和数据处理进行校准,考虑玻璃空间角度的变化对折射率测量的影响,在不考虑误差的情况下,计算时所考虑的检偏角实际上是有误差情况下的检偏角,通过误差计算得出,入射角为59.952°的精度比60°更高.

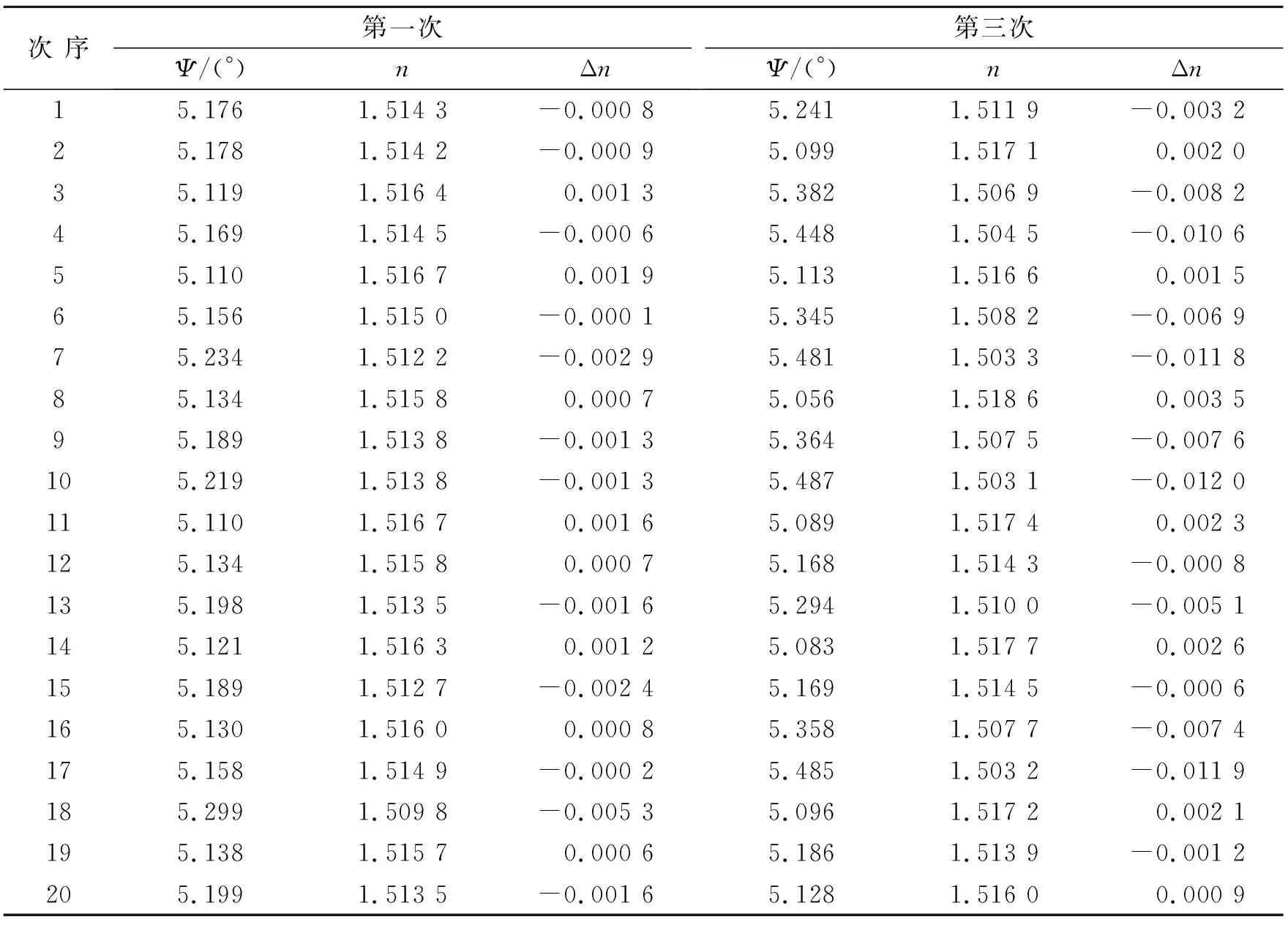
表1 椭偏法测量数据

细分误差和归零误差会引起起偏器与检偏器的转动误差.细分误差的每一个细分角转动过程中由于摩擦等各因素,会造成转动误差.细分误差引起起偏器出射光的偏振方向是否为45°,经过待测样品反射后,影响s光与p光反射情况,从而会对检偏器检测反射光的偏振方向产生影响.从入射角误差分析得出,入射角为59.952°的误差精度高,理论上的检偏角为5.274°,根据步进电机自身固有的细分误差±14″进行分析,得出实验测量偏振角为5.278°或5.270°,推算出两者的折射率误差为±1×10-4.由于存在归零误差,通过多次测量,对归零误差值进行修正,这属于系统误差.

3 结 论

基于椭偏法测量光学材料折射率的原理,对实验仪器的选取和实验过程进行设计,对实验中的发光强度变化误差、入射角精度以及起偏器与检偏器转动误差等方面进行分析，得到结论为

1) 为了提高测角精度,折射率在1.6～1.9之间,入射角固定为60°;折射率在2.4～2.7之间,入射角固定为70°,此时偏振角变化幅度大,灵敏度高.

2) 通过测量数据拟合,检偏角与发光强度成正弦曲线分布.折射率与偏振角和入射角有关,消光位置处的发光强度对检偏角影响不大,光学材料空间角度和旋转转角引起入射角的变化,细分误差和归零误差引起起偏器与检偏器的转动误差.折射率测量误差为9.16×10-4,测角精度为±30″.

参考文献：

[1] 徐均琪,冯小利.多层薄膜光学常数的椭偏法研究[J].光电工程,2009,36(2):29.

XU Junqi,FENG Xiaoli.Optical Constants of Multi-layer Thin Films Investigated by Spectroscopic Ellipsometry[J].Opto-Electronic Engineering,2009,36 (2):29.(in Chinese)

[2] 张俊莲,黄佐华,朱映彬.椭偏测厚仪确定薄膜真实厚度的分析[J].大学物理,2008,27(1):56.

ZHANG Junlian,HUANG Zuohua,ZHU Yingbin. Analyses of Determining Film Thickness by an Ellipsometer[J].College Physics,2008,27(1):56.

(in Chinese)

[3] 王芳.红外光学材料折射率测试技术研究[D].南京:南京理工大学,2004.

WANG Fang.Research on Measurement of Refractive Index of Infrared Optical Materials[D].Nanjing:Nanjing University of Science and Technology,2004.(in Chinese)

[4] 陈强.光学材料折射率的干涉测量技术研究[D].成都:电子科技大学,2003.

CHEN Qiang.Research on Interferometric Measurement of Refractive Index of Optical Materials[D].Chengdu:University of Electronic Science and Technology,2003.(in Chinese)

[5] 孟庆华,向阳.高精度测量光学玻璃折射率的新方法[J].光学精密工程,2008,16(11):2114.

MENG Qinghua,XIANG Yang.A Novel High Precision Method for Measuring Refractive Index of Optical Glass[J].Optics and Precision Engineering,2008,16 (11):2114.(in Chinese)

[6] 李宏,张金锋,尹新国.迈克尔逊干涉仪测空气折射率[J].牡丹江师范学院学报(自然科学版),2013(2):14.

LI Hong,ZHANG Jinfeng,YIN Xinguo.Measurement of Air Refractive Index with a Michelson Interferometer[J].Journal of Mudanjiang Teachers College(Natural Sciences Edition),2013(2):14.

(in Chinese)

[7] 武颖丽,吴振森.合金钢材料光学常数的椭偏测量及其修正[J].光学技术,2008,34(5):772.

WU Yingli,WU Zhensen.Measurement of Optics Constants of Alloy Steel by Ellipsometry[J].Optical Technology,2008,34(5):772.(in Chinese)

[8] 姚志,丁洪斌,杨华.椭偏法测量薄膜参数的实验改进[J].物理与工程,2013,23(5):42.

YAO Zhi,DING Hongbin,YANG Hua.Experiment Improvement in Measuring Thin Film Parameters by Ellipsometry [J].Physics and Engineering,2013,23(5):42.(in Chinese)

[9] 何龙庆.椭偏法测量薄膜厚度与折射率实验的若干探讨[J].南京晓庄学院学报,2012(6):26.

HE Longqing. Some Explorations of Measuring the Refractive Index & Thickness of Films Based on Ellipsometry[J].Journal of Nanjing Xiaozhuang College,2012(6):26.(in Chinese)

[10] 张恒.基于光度法及混合法的自动椭偏仪研究[D].广州:华南师范大学,2005.

ZHANG Heng.Study of Automatic Ellipstic Polarization Based on Spectrophotometry and Mixing Method[D].Guangzhou:South China Normal University,2005.(in Chinese)

[11] 王益朋.薄膜厚度的椭圆偏振光法测量[D].天津:天津大学,2010.

WANG Yipeng.Measurement of Film Thickness by Ellipsometry Polarization[D].Tianjin:Tianjin University,2010.(in Chinese)

[12] 张蓓蓓.基于椭偏光谱仪的石英晶体参数研究[D].曲阜:曲阜师范大学,2013.

ZHANG Beibei.Research on the Parameters of Quartz Crystal Based on Spectroscopic Ellipsometry[D].Qufu:Qufu Normal University,2013.

(in Chinese)

[13] 张建彬.高精度消光式椭圆偏振测量仪的研究与实现[D].广州:华南师范大学,2005.

ZHANG Jianbin.Research and Implementation of High Precision Extinction Elliptic Polarization Measuring Instrument[D].Guangzhou:South China Normal University,2005.(in Chinese)

[14] 王江.一种光源空间角度的测量方法[J].电子学报,2011,39(11):2692.

WANG Jiang.A Method for Measuring Light Source Angles[J].Acta Electronica Sinica,2011,39(11):2692.(in Chinese)