基于检测行为的牛结核病动力学模型分析

南瑶瑶，张 磊，侯 强

(中北大学 理学院， 太原 030051)

牛结核病是由牛型结核分枝杆菌引起的一种人兽共患的慢性传染病，在世界范围内广泛存在。它不仅影响奶牛养殖业的发展,更重要的是会导致交叉感染而使人类的健康受到严重威胁。患牛结核病的动物潜伏期一般为10～45天，有的长达数月或数年[1]。在潜伏期的染病动物是具有传染性的，而且牛结核病疫苗对牛没有完全的保护作用，因此牛结核病的净化仅靠免疫是不够的[2]。目前对动物疫病的防控措施除了免疫接种和消毒，检测扑杀也是疫病防控最重要的措施。在已有的研究中，关于免疫对动物疫病传播影响的研究较多，理论结果和应用性结果都取得较大的进展[3-6]。关于检测扑杀的动力学模型研究还比较少，已有的研究主要集中在扑杀措施对具体动物疫病传播的影响方面[4,7]。遗憾的是，在已有的研究中没有注意到扑杀前检测行为的作用和影响。因此，本文基于牛结核病传播的特征，考虑检测的真阳性率和假阳性率，建立时滞动力学模型，分析模型的稳定性和分支情况，研究检测行为会导致哪些复杂的动力学现象，并阐述这些现象背后的流行病意义。

1 模型的建立

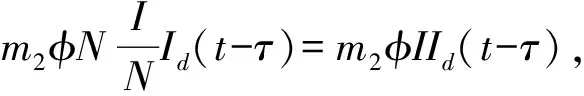
(1)

其中：A表示单位时间内种群的输入率；β表示传染率；μ表示动物的淘汰率；φ表示一个染病个体引起的检测比率；c表示被发现染病动物的捕杀率；m1表示假阳性率；m2表示真阳性率。

模型(1)的初始条件为

(2)

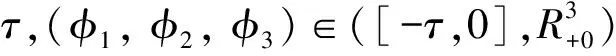
2 平衡点和基本再生数

根据下一代矩阵法，系统的基本再生数为

(3)

地方病平衡点满足下面方程：

(4)

当Rc>1时，模型有地方病平衡点：

3 平衡点的稳定性

定理2 如果Rc1,无病平衡点是不稳定的。

证明模型(1)在无病平衡点E0处的Jacobian矩阵为

特征方程为：(λ+μ)(λ-βS0+μ)(λ-m1φS0+μ+c)=0。由此可知：λ1=-μ<0。由Rc1，存在正根，无病平衡点不稳定。

构造Lyapunov函数：

对L关于模型(1)求导：

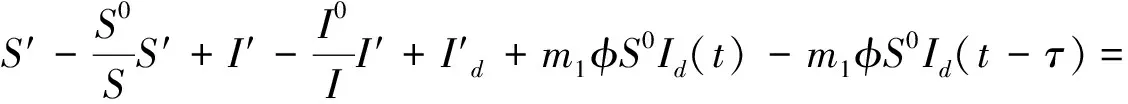
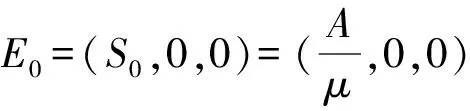
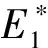
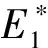
特征方程为

(λ-m1φS*e-λτ-m2φI*e-λτ+μ+c)(λ2+λ(-βS*+μ+βI*+μ)+βI*μ-βS*μ+μ2)=0

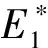
构造Lyapunov函数：

对L关于模型(1)求导：

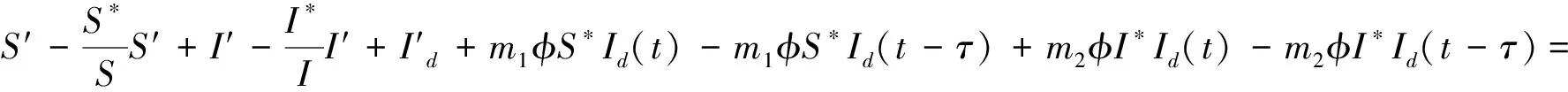
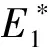
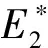
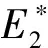
特征方程为λ3+aλ2+bλ+c=0，这里：

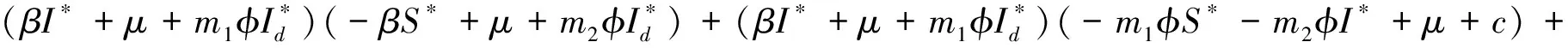
(-m1φS*-m2φI*+μ+c)β2S*I*

构造Lyapunov函数：

对L关于模型(1)求导：

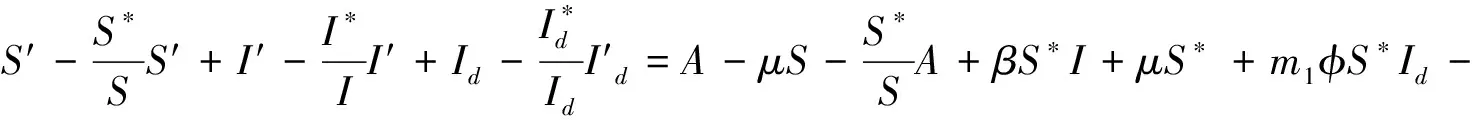
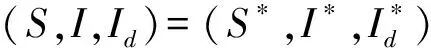
当τ>0时，模型(1)的特征方程为

λ3+a1λ2+a2λ+a3-e-λτ(b1λ2+b2λ+b3)=0

(5)

其中：

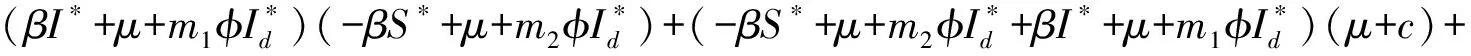
b1=m1φS*+m2φI*

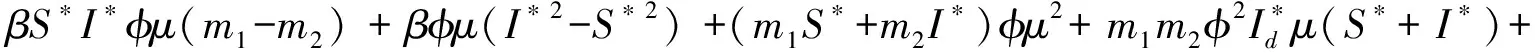
考虑纯虚根λ=ix,x>0代入特征方程后分离实部和虚部可得:

a3-a1x2=(b3-b1x2)cosxτ+b2xsinxτ

a2x-x3=b2xcosxτ-(b3-b1x2)sinxτ

(6)

两端平方相加可得

(7)

(8)

特征方程有纯虚根λ=ix,x>0则等价于f(μ)=0有正根μ=x2。这里容易得到

f′(μ)=3μ2+2M1μ+M2

(9)

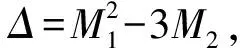
解方程(6)可得

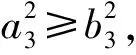
证明验证发生Hopf分支的穿越条件，根据方程(5)可得

4 数值模拟和讨论

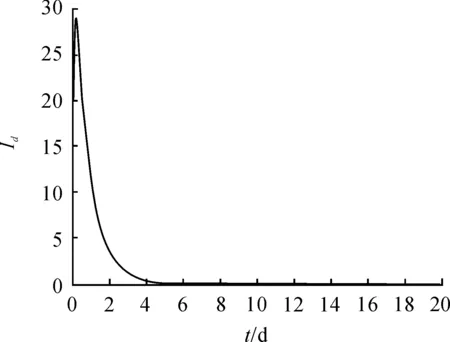
图1 τ=0

图3 τ=0.335

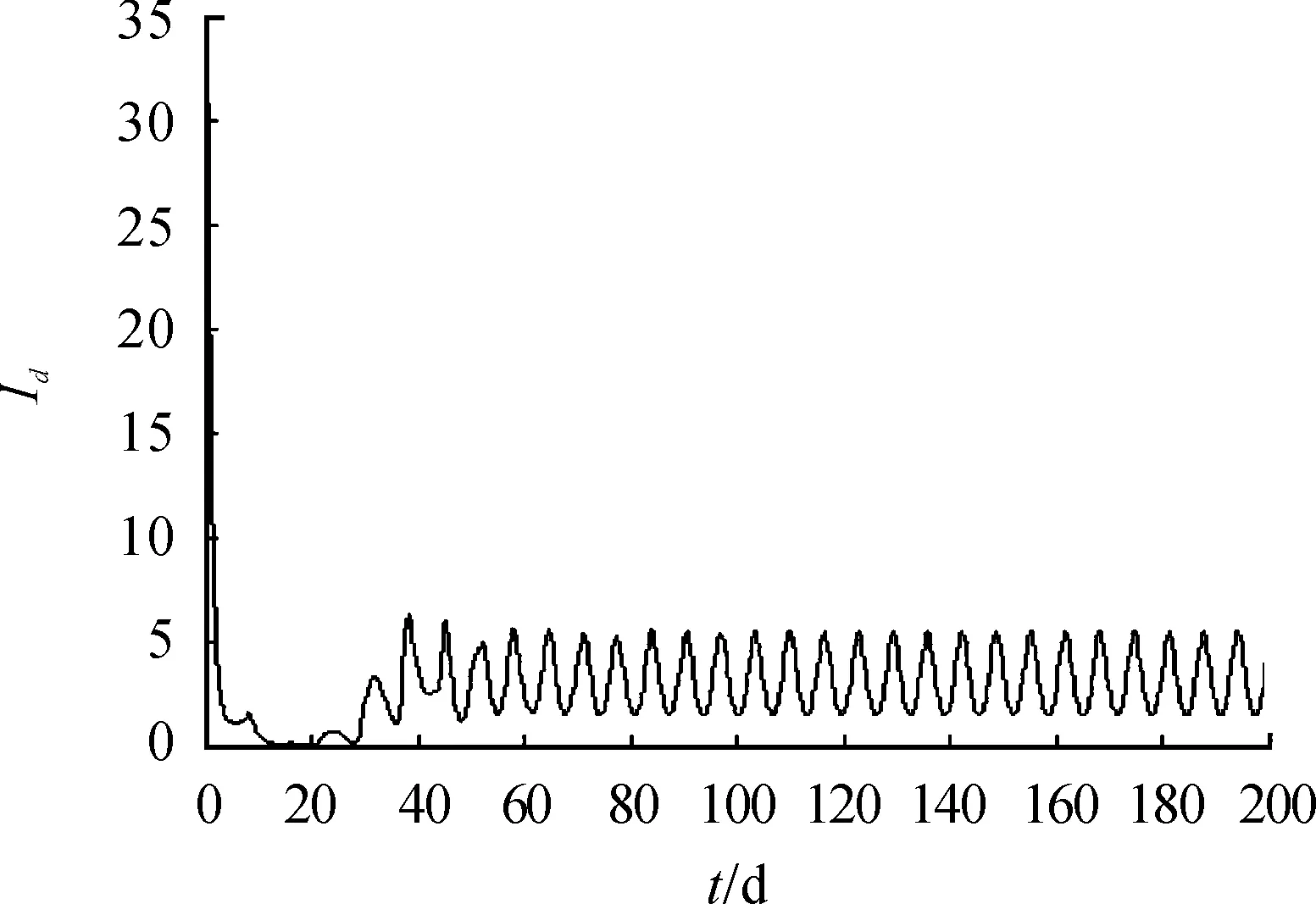
图4 τ=7.5

本文基于牛结核病传播和检测的具体特点，建立时间迟滞动力学模型。通过分析模型，发现检测不会影响模型的动力学性质，但在检测过程中的时间迟滞对动力学性质有显著影响。周期震荡行为的出现会严重影响防控措施的有效执行(例如疫病在周期运行的最低点，人们会误认为疫病开始消失)。因此，在对动物进行检测扑杀时，应尽量减少数据统计时间，避免时间迟滞的影响，使牛结核病得到更好的控制。

[1] 马洪宝.牛结核病诊治[J].中国畜禽种业,2017,13(4):125-126.

[2] 谭伟,谢志勤,谢芝勋.牛结核病疫苗研究概述[J].中国奶牛,2014(15):27-32.

[3] BREBAN R,DRAKE J M,STALLKNECHT D E,et al.The role of environmental transmission in recurrent avian influenza epidemics[J].PLoS computational biology,2009,5(4):e1000346.

[4] FERGUSON N M,DONNELLY C A,ANDERSON n R M.The foot-and-mouth epidemic in Great Britain:pattern of spread and impact of interventions[J].Science,2001,292(5519):1155-1160.

[5] ZINSSTAG J,DüRR S,PENNY M,et al.Transmission dynamics and economics of rabies control in dogs and humans in an African city[J].Proceedings of the National Academy of Sciences,2009,106(35):14996-15001.

[6] KEELING M J,GILLIGAN C A.Metapopulation dynamics of bubonic plague[J].Nature,2000,407(6806):903-906.

[7] GULBUDAK H,MARTCHEVA M.Forward hysteresis and backward bifurcation caused by culling in an avian influenza model[J].Mathematical biosciences,2013,246(1):202-212.

[8] BREBAN R.Role of environmental persistence in pathogen transmission:a mathematical modeling approach[J].Mathematical biosciences,2013,66:535-546.

[9] GUO Hongbin,LI Michael Y,SHUAI Zhisheng.Golbal dynamics of a general class of multistage models for infectious diseases,SIAM[J].Applied Mathematics,2012,72(1):261-279.