偏心对磁流变制动器性能的影响
黄 金,王 西
(重庆理工大学 机械工程学院, 重庆 400054)
磁流变液是一种由磁性颗粒、基液和添加剂组成的新型磁智能材料[1],在无外加磁场作用时,表现为一种流动性良好的牛顿流体,施加磁场后,磁流变液立刻表现出类似固体的Bingham塑性流体性质,其黏度可在几毫秒内增加几个数量级,且整个变化是可逆的[2]。一旦撤去磁场,磁流变液又迅速恢复为牛顿流体。基于磁流变液的这种力学特性,其可用于离合器、制动器等器件及传动装置。
磁流变器件是将磁流变液的流变特性运用到磁流变装置中,常见的有磁流变离合器(制动器)、磁流变阀、磁流变阻尼器等[3]。磁流变离合器是利用磁流变液作为传递动力的媒介通过电流来控制传递转矩大小的传动装置,而磁流变制动器是在磁流变离合器的基础上,将从动圆筒(外圆筒)固定作为制动圆筒,这时磁流变液产生制动转矩来抑制主动圆筒(内圆筒)的转动。目前国内外对磁流变离合器及制动器已进行了大量研究。Huang等[4]分析了圆筒式磁流变离合器和制动器的工作原理,推导了转矩传递模型,并介绍了关键尺寸的设计方法。EJ Park等[5]设计了一种磁流变制动器,这种制动器是将旋转盘沉浸在磁流变液中,同时建立有限元模型,分析了系统中磁场、流体流动和传热性能,认为设计2个旋转盘为最佳方案。李志华等[6]对圆筒磁流变制动器进行了有限元分析,得出了转筒厚度对作用于磁流变液的磁场影响。王建等[7]采用永磁体代替通电的励磁线圈,并应用ANSYS有限元分析软件对磁场进行优化,对比了有无隔磁环的影响。Tang等[8]分析表明,对磁流变液施加磁场方向的外在压力,由于挤压强化效应,磁流变液的剪切屈服应力可得到很大的提高。
虽然针对磁流变离合器及制动器国内外已进行了大量研究,但都集中在圆盘或圆筒式的磁流变液工作间隙方面,而对楔形工作间隙的磁流变液离合器及制动器性能研究较少。笔者对偏心式磁流变制动器的具体结构、工作过程及实施方案进行了一些研究[9],本文主要从理论上研究在内圆筒和外圆筒不同心时,磁流变液的剪切应力,以及偏心结构下磁流变液所能传递的制动转矩,同时对装置的制动时间进行了分析。
1 剪切应力
图1为两偏心圆筒的截面示意图,其中O1为内圆筒圆心,O2为外圆筒圆心。将外圆筒固定,内圆筒以角速度ω顺时针转动,两圆心之间的距离为e,内圆筒半径为R1,外圆筒半径为R2,则两圆筒之间的间隙即磁流变液的工作间隙:
h=ΔR(1+εcosθ)
(1)
式中:ΔR=R2-R1;偏心率ε=e/ΔR。

图1 两偏心圆筒截面示意图
在磁流变液内取一微元,微元应力分析如图2所示。

图2 微元应力分析
(2)

(3)
式中:p为切向压力;τ为剪切应力。对式(2)积分有
(4)
式中c1为积分常数。
在磁场作用下,磁流变液可用Bingham模型来描述:

(5)
γ=0τ<τ(H)
(6)

由式(4)和(5)得角速度为
(7)
式中c2为积分常数。
结合边界条件,
r=R1处,ω(r)=ω
(8)
r=R1+h处,ω(r)=0
(9)
可求出积分常数:
(10)
(11)
将式(10)代入式(4),可得内圆筒表面r=R1处的剪切应力为
(12)
当h/R1<< 1时,方程(12)可简化为
(13)
这时,运用一维雷诺方程,即可得压力p沿θ方向的分布为
(14)
式中h0为磁流变液间隙内压力最大处(即P=Pmax处)的厚度。由式(1)和(14)可得:

(15)
式中c3为积分常数。
运用Sommerfeld 积分变换对式(15)进行变换,Sommerfeld将γ定义为
(16)
由式(13)得
(17)
(18)
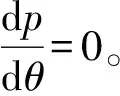
(19)
再由γ=0时,p=0;γ=π+β时,p=0,应用式(19)可确定β值。
(20)
2 制动转矩
磁流变液在各层间传递的转矩均相等,同时作用于内外筒的转矩也相等。由式(13)知,该偏心磁流变制动器所能产生的制动转矩M可表示为
(21)
式中:假设整个工作腔内的磁流变液都受到磁场作用,L为磁流变液的实际长度,根据式(1)、(19)得

(22)
在偏心工作间隙内的磁流变液在由大端流向小端时会对磁流变液的链状结构产生挤压,考虑到偏心挤压强化效应会增大10%的磁流变液剪切屈服应力[10],因此对式(21)进行修正
(23)
再次积分得
(24)
3 制动时间
制动器轴的力矩平衡关系式为
(25)
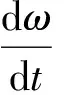
当量摩擦阻力矩Meq可表示为
(26)
式中:η∑为被制动传递系统的总传动效率;Mb为作用在制动器轴上的制动转矩。
在整个制动过程中的平均制动转矩Mm为
Jeqω-Meqtb=tbkMmax
(27)
式中:tb为制动时间;k为制动器接合时间系数,取0.5 由式(24)(25)可得出制动时间为 (28) 将式(22)代入式(26)可得: (29) 探究偏心率ε对剪切应力的影响。选用牌号为MRF-122EG的磁流变液,黏度η=0.042 Pa·s,假定偏心率ε=0.1,内圆筒半径R1=49 mm,转速ω=50 rad/s,外圆筒半径R2=50 mm,磁场强度由0~300 kA/m变化。如图3所示,一方面磁流变液的剪切应力随磁场强度的增加而增大,在0~200 kA/m时,转矩增长速率较快,而在200 kA/m之后,速率变缓,这是由于磁流变液内的磁性颗粒逐渐达到磁饱和,磁链的剪切应力不再随磁场增加而增大;另一方面,偏心后,磁流变液的挤压强化使磁流变液的剪切应力比未偏心时增大了9%左右。 图3 偏心对剪切应力的影响 磁流变制动器在未偏心时,装置所传递的制动转矩为[11]: 如图4所示,在200 kA/m时,未偏心能产生的制动转矩为47.55 N·m,而偏心挤压强化后,能产生51.33 N·m的转矩;整个过程中,磁流变制动器产生的制动转矩提高了8%左右。 图4 偏心对转矩的影响 验证偏心率对制动时间的影响,比较偏心和未偏心时的制动时间。同样假设偏心率ε=0.1,结合时间系数k=0.7,传动效率ηΣ=0.98,制动器轴传递的转矩Mb=15 N·m,当量转动惯量Jeq=0.5 kg·m2。同样未偏心时,式(27)中: 当无外加磁场作用时,制动器只能依靠磁流变液的黏度来制动,这时未偏心的制动器制动时间为59.79 s,而偏心率为0.1的制动器制动时间为53.22 s。如图5所示,在200 kA/m时,未偏心的制动器制动时间为0.74 s,而偏心挤压强化后的磁流变制动器制动时间为0.68 s。综合来看,偏心磁流变制动器的制动时间比未偏心的制动时间缩短了10%左右。 图5 偏心对制动时间的影响 基于Bingham模型和一维雷诺方程,对磁流变液在两偏心圆筒间的剪切应力进行分析,并建立了数学模型,同时比较了偏心制动圆筒的制动性能和普通同心圆筒的制动性能,得出以下结论: 1) 偏心挤压强化后磁流变液的剪切应力比同心时的剪切应力综合增大了9%左右。 2) 磁流变制动器的制动转矩在考虑了楔挤压强化效应后,偏心圆筒磁流变制动器比同心圆筒磁流变制动器产生的制动转矩提高了8%左右。 3) 在磁流变液产生流变效应后,偏心圆筒磁流变制动器比同心圆筒磁流变制动器制动时间缩短了10%左右。 [1] 唐龙,卢利平,岳恩,等.磁流变液的研究与应用[J].重庆理工大学学报,2013,27(12):44-48. [2] 王鸿云,郑惠强,李泳鲜.磁流变液的研究与应用[J].机械设计,2008(5):1-4,8. [3] 熊超,申小海,郑坚,等.磁流变器件设计中的关键技术[J].磁性材料及器件,2008,39(4):37-39. [4] HUANG Jin,ZHANG Junqian,YANG Yan,et al.Analysisand design of a cylindrical magnetorheological fluid brake[J].Journal of Materials Processing Technology,2002:559-562. [5] PARK E J,STOIKOV D,LUZ L F D,et al.A performance evaluation of an automotive magnetorheological brakedesign with a sliding mode controller[J].Mechatronics,2006,16(7):405-416. [6] 李志华,朱丰友,郭林超.圆筒式磁流变制动器结构设计[J].机械设计与研究,2008,24(6):49-51. [7] 黄金,王建,陈松.圆筒式磁流变制动器磁路设计与优化分析[J].机械传动,2017,41(7):106-110. [8] TANG X L,ZHANG X Z,TAO R.Structure-Enhanced yield strength of MR fluids[J].Journal of Applied Phy-sics,2000,87(5):2634-2638. [9] 黄金,王西,周轶.一种偏心式磁流变制动器[P].中国专利:ZL201720304157.2.2017-11-17. [10] 黄金,袁发鹏,周轶.圆盘与圆筒复合温控式磁流变传动性能研究[J].重庆理工大学学报(自然科学),2017,31(2):39-45. [11] 黄金,廖林清,林昌华.圆筒式磁流变离合器的设计分析[J].功能材料,2006(5):760-761,764.
4 结果与讨论



5 结论

