一种高效的顶点偏心率计算方法

刘 冬，杜 明，王志军，周军峰

(东华大学 计算机科学与技术学院，上海 201620)

0 引言

在无向图G=(V,E)中，任意两个顶点u、v间的最短路径dist(u,v)指的是从u到v的路径的最小长度。从u出发的一条最长最短路径则是顶点u的偏心率，得知顶点的偏心率有助于分析图的其他特征，比如图的中心性、半径和直径等。顶点的偏心率越小，它在图中的中心性越高，表示该顶点距离其他顶点更近。在一些实际的应用场景里，偏心率求解是十分重要的，比如寻找社交网络中有影响力的人、流行病关系网络中的关键顶点或网络拓扑图中的重要站点等。

现有偏心率求解的算法主要分为近似算法[1-5]和精确算法[6-13]。针对精确算法，文献[13]提出了ECC算法，该算法在图中设置了参考顶点池，并构建参考顶点的全局BFS索引，计算顶点x的偏心率时，选取距离x最近的参考顶点，然后按照该参考顶点索引将所有顶点分为两个部分，最后分别计算出x对这两个部分的局部偏心率，局部偏心率的最大值则为x的偏心率。该算法虽然避免了使用大量的BFS遍历来求解偏心率，但由于其索引构建代价高和顶点计算规模大的问题，所以导致该算法在大图中计算效率较低。

针对上述算法中存在的问题，本文提出一种基于子图划分思想的偏心率求解算法。其主要思想是：首先选定K个参考顶点，将图划分为以这K个点为中心、互不相交的子图，并构建基于参考顶点的局部BFS索引。在计算前，利用顶点合并策略对图中的顶点进行合并以降低计算规模，并对参考顶点索引进一步优化。在计算时，利用索引先得出待计算顶点对每个子图的局部偏心率范围，并基于索引进行剪枝，在较小范围内计算偏心率。实验表明，本文提出的算法降低了索引构建的规模，改进了求解偏心率的效率，比现有求解偏心率的算法更加高效。

1 背景知识及相关工作

1.1 问题定义

1.1.1 数据模型及基本概念

给定一个无向无权图G=(V,E)，其中V= {v1,v2,… ,vn}是图中的顶点的集合，e(u,v)∈E表示u、v之间存在一条边，边的权值默认为 1，|V|用来表示图中的顶点个数，|E|用来表示图中的边个数。如图1所示。

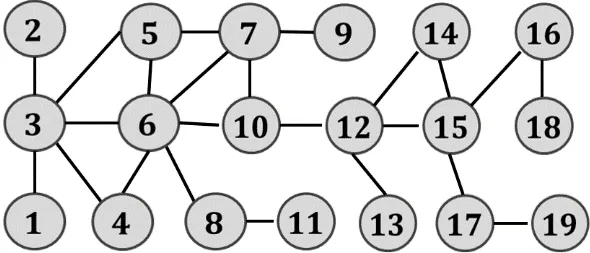
图1 无向无权图 G = (V, E)Fig.1 undirected and unweight graph G = (V, E)

定义1最短路径：对于图G中的任意两个顶点u、v（∀u,v∈V），u、v间的最短路径是从u到v的路径中最短的一条，记做d(u,v)。

定义 2偏心率：对于图G中任意顶点u，其偏心率值是从u出发的一条最长最短路径的长度，记做ecc(x)，且有ecc(u) ≥d(u,v) ,∀v∈V。如图2所示，顶点上方的数字表示该顶点的偏心率值。

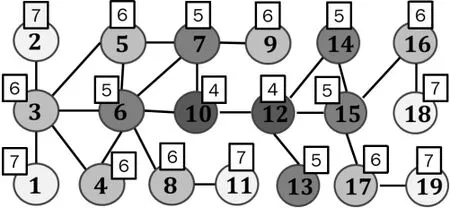
图2 所有顶点的偏心率值Fig.2 Eccentricity of all vertex

定义3偏心率不等式：对图G中任意三个顶点u、v和w，总满足d(u,v) ≤d(v,w) +d(w,u)。对图G中任意两个顶点u、v，有

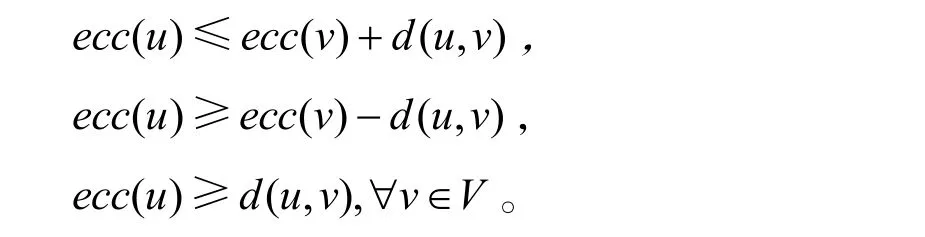
定义4局部偏心率：设V1为图G的一个子顶点集，即V1∈V，对 ∀x∈V,x的在V1上的局部偏心率记做pecc(x|V1) ，则有pecc(x|V1) ≤ecc(x)，另外，pecc(x|V) =ecc(x)。

推论1将图G的顶点集V的划分为V1,V2两个子集，即V=V1∪V2，根据定义4，对∀x∈V，有ecc(x) ≥pecc(x|V1),ecc(x) ≥pecc(x|V2)， 当pecc(x|V1)≥pecc(x|V2)时,ecc(x) =pecc(x|V1)，否则，ecc(x) =pecc(x|V2)。

证明：因为V=V1∪V2，且ecc(x)≥d(x,v),∀v∈V， 则 有pecc(x|V1) ≥d(x,v) ,∀v∈V1和pecc(x|V2)≥d(x,v) ,∀v∈V2， 所 以ecc(x)=max{pecc(x|V1),pecc(x|V2)}。

推论2设V1,V2为V的子集，有V=V1∪V2，对∀u,v∈V，则当pecc(u|V2) ≥pecc(v|V1) +d(u,v)时，有ecc(u) =pecc(u|V2)。

证明：根据推论1，可以得出，对∀u,v∈V，有pecc(u|V1) ≤pecc(v|V1)+d(u,v)；当pecc(u|V2)≥pecc(v|V1) +d(u,v)时，有pecc(u|V2) ≥pecc(u|V1)，根据推论2，ecc(u) =max{pecc（u|V1）,pecc(u|V2)}，则ecc(u) =pecc(u|V2)。

如果给定的图G存在孤立顶点，即存在孤立顶点u，使得u与其他任意顶点间，导致所有顶点的偏心率变成+∞，所以本文使用数据集均为为连通图或图的最大连通分量。

1.1.2 PLL算法

1.2 相关工作

现有偏心率求解的算法可以追溯到2011年，Frank W. Takes等人[7]根据三角不等式推导，首次提出了偏心率不等式，为之后研究偏心率求解的问题提供了思路。

K. Henderson提出了 OPEX算法[8]。该算法提前设立一个阈值 t，根据顶点的排序结果进行BFS遍历，并使用遍历结果收敛其他顶点的偏心率范围。当所有顶点偏心率范围的差值小于等于2t时结束，当t=0时，该算法的结果为精确值。Frank W. Takes等人[10]基于之前提出的偏心率范围，提出了偏心率求解算法，该算法反复选取最大上限和最小下限的顶点进行BFS遍历，根据遍历的结果收敛其他顶点的偏心率范围。以上两个算法由于大量使用BFS遍历，导致计算效率低下，不适用于较大规模的图。

针对上述问题，Wentao Li等人[13]提出了ECC算法，其基本思想是，首先构建图的PLL查询索引，避免大量使用BFS遍历。其次从图中选择前K个最大度的顶点作为参考顶点，同时构建参考顶点的全局BFS索引，如图3所示。接着在计算时选择距离待计算顶点最近的参考顶点，并将对应的索引划分为前后两个部分W1、W2，分别得出待计算顶点对于这两个部分的局部偏心率作为全局偏心率范围。最后，沿着索引逐渐向前扩展W2，使得u的全局偏心率下限向上收敛；缩小W1，使得u的全局偏心率上限向下收敛，当偏心率上下限相等时可得出顶点u的偏心率值。ECC算法存在以下两点问题：1）参考顶点索引构建代价高；2）索引过长，计算时的索引平均查找代价较高，即改变W1、W2的次数较多，导致偏心率计算的效率较低。

图3 参考顶点6和15的全局BFS索引Fig.3 The whole index of reference node 6 and 15

2 偏心率求解算法ECC-DIS

2.1 子图划分策略

针对现有算法参考顶点索引构建代价高，索引过长的问题，提出了子图划分的策略及相应算法SGR（Subgraph Refpool）。其主要思想是，首先选定K个顶点作为参考顶点，其次围绕这K个顶点向外扩展，将整个图G划分为互不相交的K个子图，最后每个子图构建基于参考顶点的局部BFS索引，相当于每个顶点只参与一次索引构建，索引规模是ECC算法的1/K。相应的算法如下：

算法1：SGR(G,K)

输入：G=(V,E)，K

输出：参考顶点的局部偏心率及其索引peccz，Lz， ∀z∈refpool

初始化：W←V，Q=∅，Qz=∅，dis=2，/*Q和Qz的存储结构都是，key是顶点编号，value是最短路径长度*/

1) forif r om 1to Kdo

2)z←W中度最大的顶点

首先，从未被划分的顶点中选择度最大的顶点作为参考顶点z，设z的未划分邻居顶点为t，将(z,0)和(t,1)加入到参考顶点索引Lz中，上述流程执行K次，得到K个子图(第1-9行)。接着，分别使用 BFS遍历围绕这 K个参考顶点向外拓展，将遍历到的顶点划分到各自的子图中，并构建相应的索引，当覆盖所有顶点时，子图划分完成（第10-20行）。

例如，对图1的G，假设需要选取2个参考顶点，首先选取度最大的顶点6作为参考顶点，将6的邻居顶点划分完成后，接着选取剩余度最大的顶点为15作为参考顶点，然后通过子图划分可将图划分为2个部分，如图4所示，根据子图划分结果构建参考顶点的局部BFS索引，如图5所示。从划分结果可以看到，图G被划分成了 2个不相交的子图。由于每个顶点只参与了一次构建，所以索引规模是ECC算法的1/2。

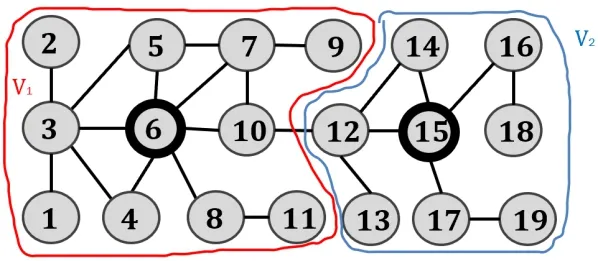
图4 子图划分结果（K=2）Fig.4 The result of subgraph partitioning

图5 参考顶点6和15的局部BFS索引Fig.5 The partial index of reference node 6 and 15

2.2 单个顶点偏心率求解算法

基于子图划分的思想，提出了相应的偏心率求解算法EccComp（Eccentricity Computation）。该算法首先根据子图划分所构建的索引，得出待计算顶点对于每个子图的局部偏心率范围。然后基于索引进行剪枝，在较小范围内计算偏心率。该算法的伪代码如下：

算法2：EccComp(G,K,PLL,Lz,x)

输入：G=(V,E)，K，PLL，Lz，x

输出：顶点x的偏心率ecc(x)

//Lzi= {v1,v2,… ,vT}，d(z,x)用PLL索引查询

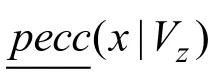
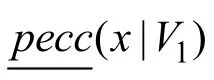
图6 计算顶点12的偏心率Fig.6 Computing the eccentricity of vertex 12

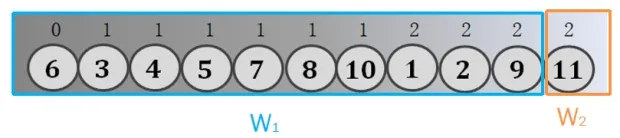
图7 参考顶点6的索引划分Fig.7 Partitioning the index of reference node 6

2.3 基于顶点合并策略的优化

在无向无权图G=(V,E)中，存在一些特殊的“末端”顶点，这些顶点可以分为两类，第一类是在初始图中度为1的顶点（比如图4中的顶点1），第二类顶点是在合并图中所有度为1的顶点后，度数变为1的顶点（比如图4中的顶点8），这里的“合并”并不是将图中的顶点删除，而是暂时忽略合并的顶点和该顶点相连的边，接受合并的顶点称为根顶点，如图9所示，顶点3为顶点1的根顶点。不难看出，第一类顶点到任意顶点的最短路径必经过其根顶点，因为它们只有一个邻居顶点；第二类顶点则不同，它们有多个邻居顶点，最短路径不一定会经过其根顶点。根据以上分析，提出了顶点合并策略及算法，在根顶点的偏心率计算完成后，可直接推理出第一类顶点的偏心率，比较根顶点的偏心率和合并顶点深度的关系能判断第二类顶点的偏心率是否与根顶点相关。该策略减少了偏心率计算的顶点规模，改进了偏心率计算的效率。相应算法如下：

算法3：NodeMerge(G,di)

输入：G=(V,E),di∈(1,n),

输出：合并顶点表NodeM[v]，合并顶点深度Deep[v] ,∀v∈V

1)Q← ∅,W←V

首先，根据给定的初始图G=(V,E)，从所有顶点中查找di∈(1,n)为1的顶点（第1-4行），将它们合并到未访问的邻居顶点j中，可知顶点j为它们的根顶点，修改顶点j的合并顶点深度Deep[j]。接着，将dj减1，并判断j的剩余度数是否为1，若为1，说明j也属于“末端”顶点，同样，将j合并到其未访问的邻居顶点中，并修改邻居顶点的合并顶点深度。最后，反复执行上述合并流程，直到图中不存在度为1的顶点为止，W是非合并顶点集，表示只需要计算在W中的顶点偏心率（第5-17行）。

例如，对图1中的G=(V,E)进行顶点合并。首先，合并图中度为1的顶点，如图8所示。其次，根据合并的结果，继续合并新产生的“末端”顶点。最后，反复合并新的度为1的顶点，当图中不存在该类顶点时，合并流程停止，合并结果如图9所示，顶点后面括号中代表合并的顶点，合并后偏心率计算的顶点规模由19个变为9个。

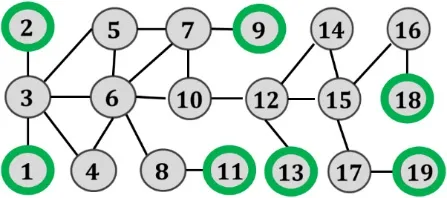
图8 合并度为1的顶点Fig.8 Merging the vertex of degree is 1

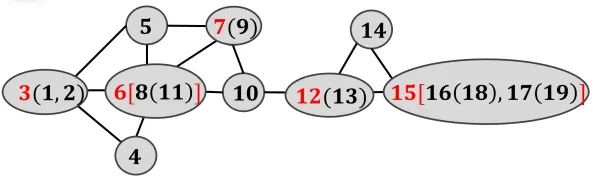
图9 合并结果Fig.9 The result of merge

2.4 偏心率计算方法

结合上述三个算法，设计出求解所有顶点偏心率的完整算法ECC-DIS（Eccentricity Distribution）。具体思想是，首先使用顶点合并策略，降低偏心率计算的顶点规模。其次划分出以K个参考顶点为中心、互不相交的子图，并对每个子图构建基于中心顶点的索引。在计算时利用索引先得出待计算顶点x对于每个子图的局部偏心率范围，最后基于索引进行剪枝，在较小范围内计算偏心率。ECC-DIS算法的执行流程如下：

算法4 ECC-DIS(G,K)输入：G=(V,E),K

输出：ecc(v),∀v∈V

初始化：Q=∅

首先，构建G=(V,E)的PLL查询索引，使用NodeMerge算法合并图中的“末端”顶点，通过SGR算法划分子图以及构建参考顶点索引（第1-3行）。其次，计算非合并顶点集W中顶点w的偏心率值，如果顶点w的合并顶点表NodeM[w]不为空，表示w是根顶点，则需要判断ecc(w)是否等于w的合并顶点深度Deep[w]，若不相等，表示NodeM[w]中被合并顶点x的偏心率ecc(x)=ecc(w)+ 1 ，并且根据ecc(x)可以继续得出NodeM[x]中被合并顶点的偏心率值（第5-15行）；若相等，表示距w最远的顶点可能会在以w为根顶点的路径内，即无法判断出该路径内的顶点偏心率是否与ecc(w)相关，此时将NodeM[w]中的所有顶点重新加入到非合并顶点集W中，表示它们的偏心率需要计算（第16-18行），最后，继续计算W中的顶点偏心率，直到W为空集（第4行），返回所有顶点v的偏心率ecc(v)（第19行）。

3 实验分析

3.1 实验环境

本次实验所采用硬件平台是Intel(R) Xeon(R)Silver 4208 CPU @ 2.10GHz，gcc版本为 4.8.5，操作系统版本为Red Hat 4.8.5-39。用于实验比对的算法有（1）现有偏心率求解方法ECC；（2）本文提出的算法ECC-DIS算法。以上实验算法均采用C++语言实现。

3.2 数据集

本次实验使用了11个真实数据集，Gowalla、Email-EuAll、Dblp、Web-Google、Youtube、WikiTalk-temporal、Skitter、Wikitopcat和 WikiTalk来源于斯坦福大型网络数据集[15]；05citeseerx描述的是蛋白质交互网络；Dbpedia数据集描述的是知识图谱。表1列出了这些数据集的基本信息，所有图都被转化成了无向无权图，其中，|V|和|E|分别是数据集的顶点个数和边个数，Merged Node为顶点合并的个数。从表中可以看到，大部分数据集的顶点合并个数在3%-40%之间。

表1 数据集统计信息Tab.1 Statistics for the dataset

3.3 性能分析与比较

3.3.1 偏心率计算的总时间对比

表2中展示了ECC算法和ECC-DIS算法在偏心率计算时的时间比较，其中ECC算法分为三个部分Refpool、EccOneNode和Total；ECC-DIS分为 SGR和 EccComp，分别是参考顶点构建方法、偏心率求解方法和两者的总时间，所有时间均用秒(s)表示，具体实验结果分析如下所示。

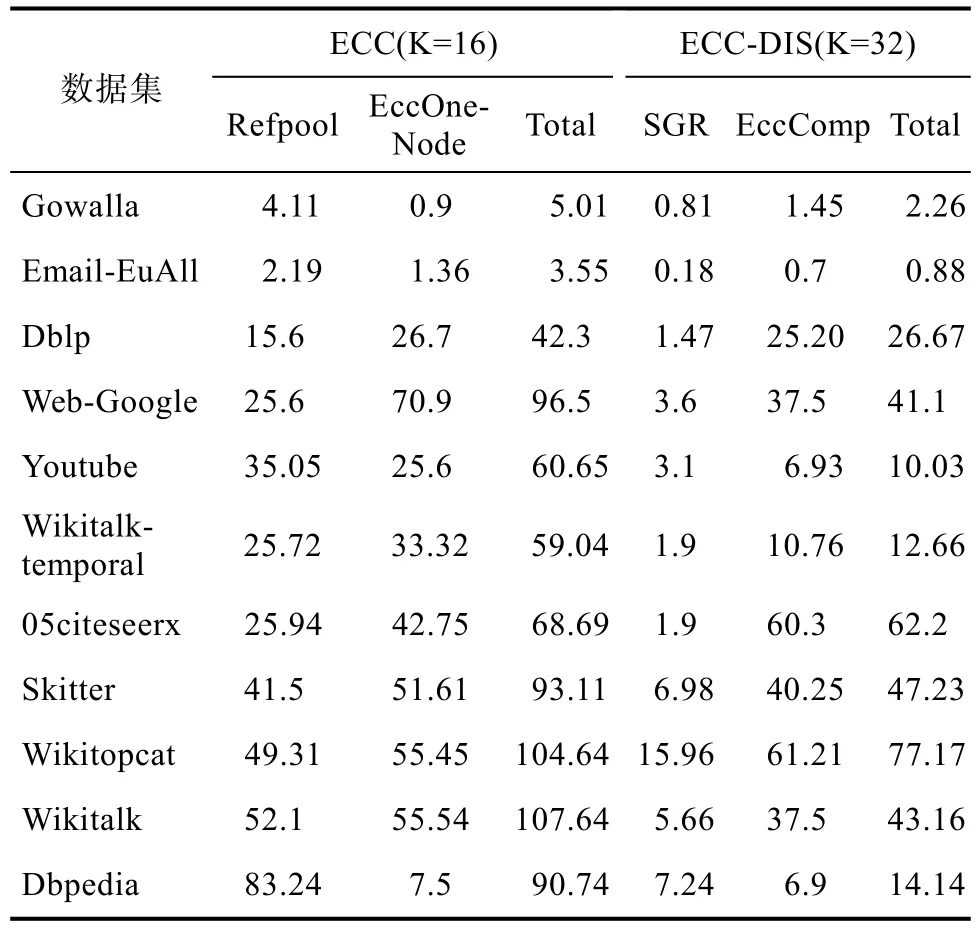
表2 偏心率计算的时间比较/sTab.2 Time comparison of eccentricity computation

在构建参考顶点索引的时间上，SGR算法比已有的Refpool算法快了3倍到13倍左右。在偏心率求解的时间上，除了在 Gowalla数据集上EccComp算法和EccOneNode算法的时间相近；在其他数据集上，EccComp算法比 EccOneNode算法快了1.2倍到3.6倍左右，这是因为切换子图的开销比较大，所以计算偏心率的时间并没有优化太多。在算法的总时间上，ECC-DIS算法比ECC算法快1.2倍到6.4倍左右。

3.3.2 参考顶点索引规模及构建时间对比

表3展示了Refpool算法和SGR算法的参考顶点平均索引规模和索引构建时间。其中，取K=16，参考顶点平均索引规模表示K个参考顶点索引内元素的平均个数，索引构建时间的单位是秒(s)。

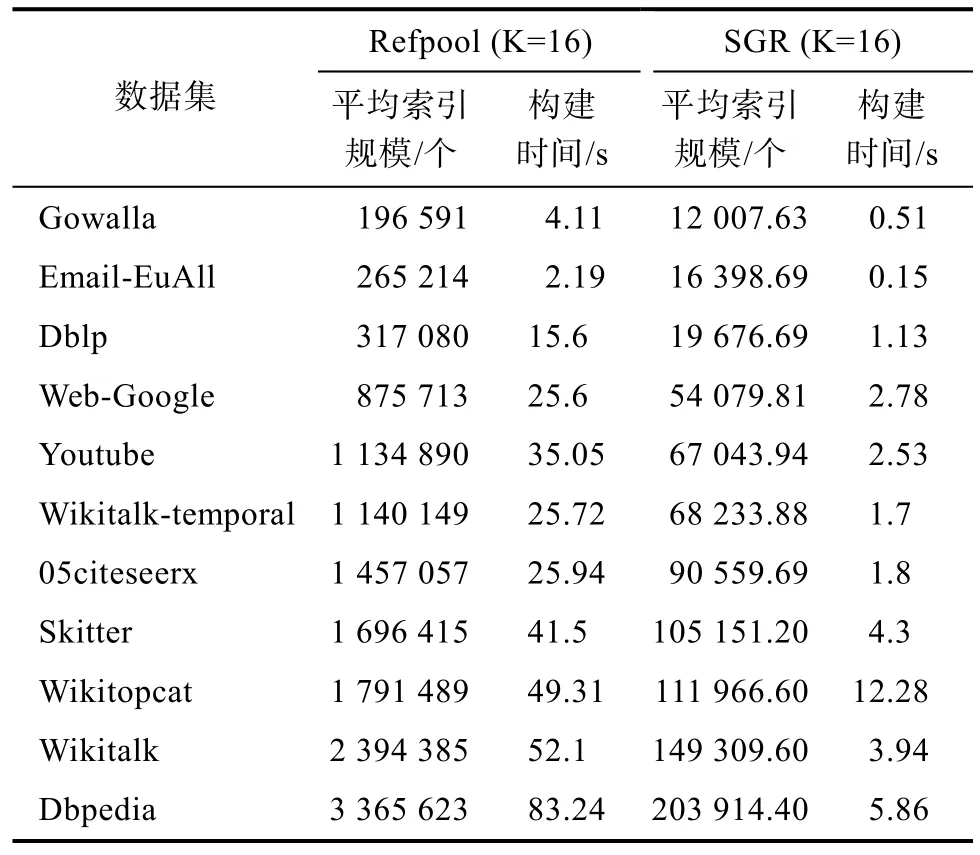
表3 不同数据集上的索引规模及构建时间Tab.3 Index size and build time on different data sets

由实验结果可知，在 K=16的情况下，SGR算法比 Refpool算法的索引规模小了 16倍到 17倍左右，在索引构建时间上，算法加速倍数在 4倍到15倍之间，因为SGR算法不仅需要对顶点进行K次排序来选出K个参考顶点，还需要根据子图划分构建索引，导致加速倍数总低于索引优化倍数。

3.3.3 参考顶点索引平均查找长度对比

图10展示了ECC算法和ECC-DIS算法在计算偏心率时参考顶点索引的平均查找长度，其中ECC算法中的K=16，ECC-DIS算法中的K=32，图的横坐标是不同数据集，纵坐标是计算偏心率时每个顶点的索引平均查找长度。

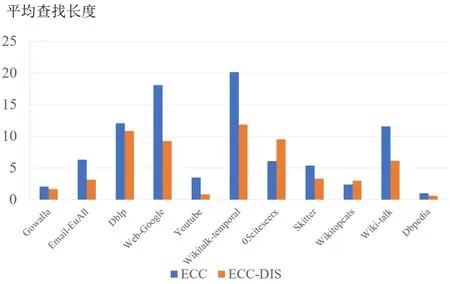
图10 不同数据集上索引平均查找长度/个Fig.10 The average search length of index in different dataset

由实验结果可知，在05citeseerx和Wikitopcat数据集上，ECC-DIS算法与ECC算法的索引平均查找长度相近，在其他数据集上，ECC-DIS算法的索引平均查找长度普遍要比 ECC算法的平均查找长度少，优化倍数在1.2倍到4倍之间。

4 结论

本文针对现有偏心率求解算法中存在的索引构建代价高、计算效率低的问题，提出了基于子图划分的偏心率求解方法ECC-DIS，降低了参考顶点的索引的规模和构建时间，通过对顶点进行合并，提高了偏心率的计算效率。实验结果表明，ECC-DIS算法中的索引规模是现有算法的 1/K，在偏心率计算的总时间方面，ECC-DIS算法比现有算法快了1.4倍到6倍左右。