静止轨道共位卫星东西位置保持优化控制

石善斌,韩秋龙,吕斌涛

(1.解放军信息工程大学 测绘学院,河南 郑州 450052;2.北京跟踪与通信技术研究所,北京 100094)

0 引言

多星共位是指在通常仅放置1颗卫星的窗口(经纬度±0.1°)内保持2颗或以上的卫星[1]。主要用于解决逐渐增加的静止轨道卫星与有限的轨道弧段间的矛盾。随着静止轨道卫星数量的增多,多星共位将会更广泛地应用。由于摄动因素的影响,共位星群需进行定期的南北保持和东西保持,在满足卫星间相互隔离的前提下使其不超出位置保持窗口[2]。其中,共位卫星的东西保持常采用太阳指向近地点策略对其偏心率矢量进行控制,但该方法主要确定了在1 d中对卫星进行控制的最优时刻,而对其他位置保持参数(如控制周期、偏心率控制圆半径等)及共位卫星保持参数未作优化[3、4]。本文基于静止轨道多星共位任务中东西位置保持中能量消耗与保持参数间关系的分析,提出了共位卫星东西位置保持参数的优化设置方法。

1 倾角、偏心率隔离

对地球静止轨道卫星,其运动特性通常采用同步根数：平经度漂移率D、偏心率矢量e、倾角矢量i和平恒星时角(平赤经)L描述,有

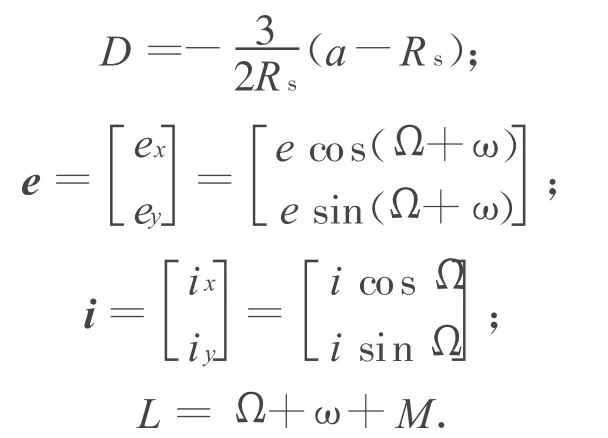
式中：Rs为地球静止轨道半长轴;a,Ω,ω,M分别为卫星的轨道半长轴、升交点赤径、近地点幅角和平近点角。

从轨道隔离的角度来看,只要任意两星间能实现隔离,就可实现多颗卫星的共位运行。倾角、偏心率隔离方法的基本原理是：所有卫星共同占用整个经度保持范围,保持任意两星的偏心率矢量差Δe和倾角矢量差Δi不为0,利用Δi使卫星在不同的轨道平面产生法向方向的隔离,利用Δe产生径向和经度向的隔离,使两星轨道平面交叉处也产生隔离,从而保证任两星间的相互隔离[5]。

本文以常用的子午面内倾角、偏心率隔离方法为例,讨论静止轨道共位卫星东西位置保持参数的优化设置方法。子午面内倾角、偏心率隔离方法要求各共位卫星间的Δe,Δi平行,由Δe产生共位卫星的最小间隔距离为Rs|Δe|。子午面内倾角、偏心率隔离方法倾角与偏心率矢量隔离设置分别如图1、2所示。图中：S1,S2,S3为3颗卫星。

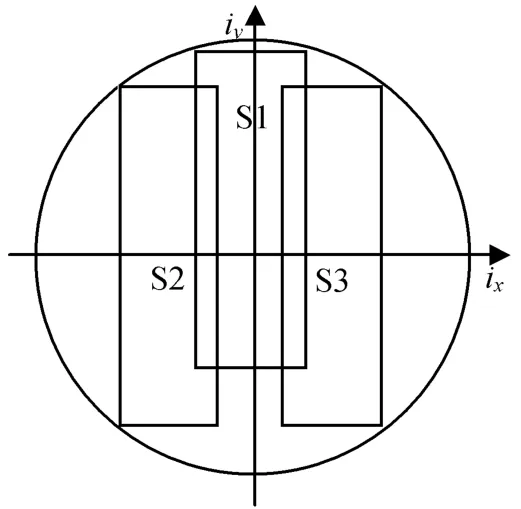
图1 倾角隔离Fig.1 Inclination vector control box

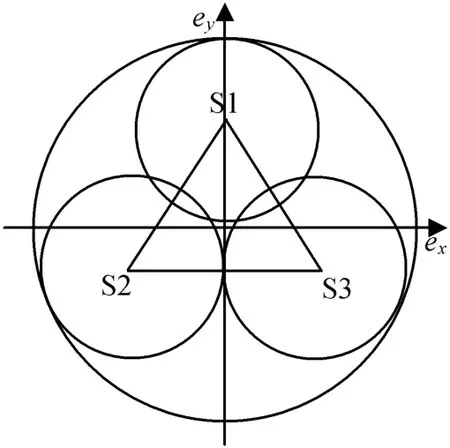
图2 偏心率隔离Fig.2 Eccentricity vector control circle

2 东西位置保持

静止轨道卫星在东西向的漂移由两部分组成：一是地球形状摄动使卫星平经度产生漂移,另一是太阳光压产生的偏心率摄动,引起卫星的经度日周期振荡。卫星经度位置保持控制是,给定定点经度位置为λs和位置保持半宽Δλs,使卫星不漂移出控制范围

2.1 平经度保持策略

静止轨道卫星的平经度主要受地球非球形引力的田谐项的影响。平经度保持主要是利用东西机动校正卫星的漂移率,将一颗地球静止轨道卫星保持在一较窄的轨道窗口内。由于共位星群中卫星的相对距离较近,所受田谐项加速度基本相同。且在较小的轨道窗口(如1°)内卫星所受田谐项加速度近似相等,可认为卫星所受的地球椭状摄动力在轨道保持周期内为一常值。在地球非球形摄动的作用下,共位星群整体的经度漂移运动与一颗静止轨道卫星相同,为一漂移极限环(如图3所示),可表示为

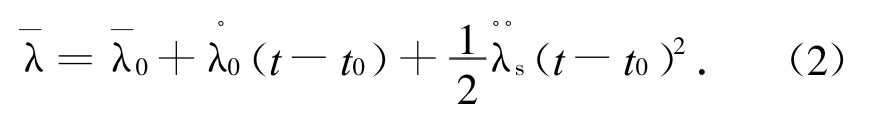
每次经度控制所需平经度漂移率的修正量

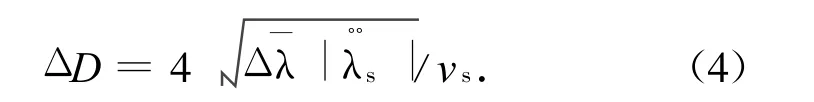
图3 经度漂移极限环Fig.3 Mean longitude evolution

2.2 偏心率保持策略

卫星轨道偏心率矢量主要受太阳光压的影响。在太阳光压作用下,卫星的平偏心率增量垂直于阳光,指向太阳视运动方向。1 d内平偏心率增量近似为常值,平偏心率矢量的端点跟随太阳视运动,1年内在赤道坐标面上描绘成一个偏心率摄动圆。摄动圆圆心位于通过初始平偏心率矢量的太阳光方向。因此,在太阳光压作用下,平偏心率增量虽为常值,但平偏心率并不一定为常值,而取决于初始平偏心率的指向及其幅值。

在静止轨道卫星偏心率矢量保持策略中,太阳指向近地点策略是一种较常用的方法。如图4所示,太阳指向近地点策略使卫星的平偏心率矢量在控制周期内始终保持在偏心率控制圆内,并使控制圆圆心至平偏心率矢量端点连线的平均方向指向太阳方向。该方法在卫星面质比稳定时有很强的周期性,每次偏心率控制的增量基本相同并与太阳方向垂直,利于卫星测控的实施。

图4 太阳指向近地点策略Fig.4 Sun pointing perigee strategy

由图4可知：太阳在1个保持周期T转过的角度nST与太阳滞后角β满足关系

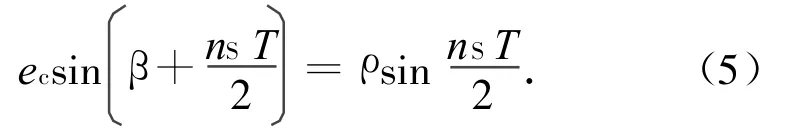
式中：ec为卫星控制圆半径;ρ为卫星摄动圆半径;nS为太阳视运动平均速度,且nS=0.017 2 rad/d。

由式(5)可知：当β+n S T/2=π/2时,偏心率保持周期最长,且

当T确定时,可由式(5)求出偏心率的控制目标为：

a)太阳滞后角

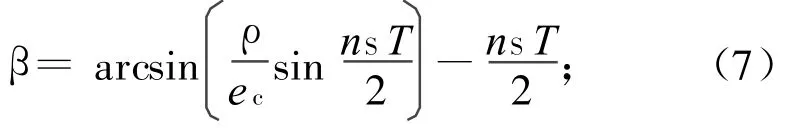
b)每次偏心率修正量约为

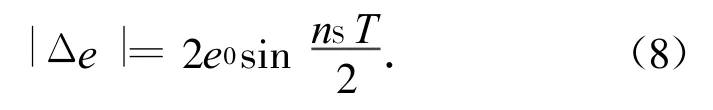
当偏心率保持周期已定时,对偏心率摄动圆半径为ρ的卫星,可将其偏心率控制在半径最小为ecmin的控制圆内,且

2.3 东西保持机动

切向推力和径向推力均属于平面内机动。采用切向推力的机动称为切向控制(亦称东西控制或经度控制),可改变卫星的经度漂移率和偏心率矢量。径向推力的机动仅改变卫星的偏心率矢量,但同样大小的径向推力,只能达到切向推力的一半效果。与径向控制相比,切向控制的效率更高[6]。因此,静止轨道卫星的东西保持机动主要依靠切向推力实现,很少采用径向推力。

切向控制对静止轨道根数的影响可用轨道机动增量表示。切向推力Δvt引起的平经度漂移率和偏心率矢量分别为

式中：vS为静止轨道速度;sb为推进时刻卫星恒星时角;Δvt为切向推进速度,向东为正,向西为负。

由于切向机动不仅能引起偏心率矢量的变化,而且可导致轨道漂移率(半长轴)的变化,因此为优化地面测控工作并减少燃料消耗,理想状态的东西保持通常使卫星平经度保持控制周期与偏心率保持周期相同,利用平面内机动燃料消耗最优准则,同时对卫星的偏心率矢量和平经度进行保持控制[5]。

3 保持参数优化设置

本文将共位卫星东西位置保持优化的目的确定为：在满足多星共位任务和减少测控工作量的前提下,使东西位置保持所消耗的能量最小。

东西位置保持控制所需的速度冲量主要用于平经度和偏心率矢量的保持控制。由平面内机动燃料消耗最优准则可知：静止轨道卫星在1年中用于东西位置保持所需速度冲量的总量Δvew为平经度和偏心率矢量保持控制所需速度冲量较大的部分,可表示为

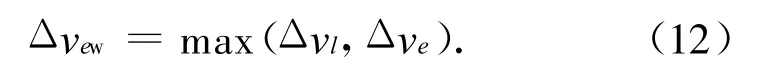
式中：Δve,Δvl分别为共位卫星平经度和偏心率矢量的保持控制平均1年所需的速度冲量,且

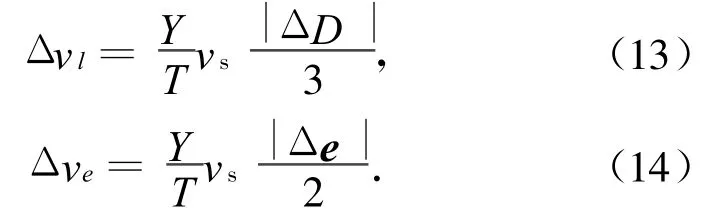
此处：Y为1年的天数(约365.25 d);|Δe|为每次东西位置保持卫星偏心率矢量的增量;|ΔD|为每次东西位置保持卫星平经度漂移率的改变量。

将式(3)、(4)、(10)代入式(13),有

将式(8)代入式(14),并综合式(11)有

由此可知：Δvew主要与定点位置的平经度漂移率、卫星偏心率控制圆半径ec,T和卫星的偏心率摄动圆半径相关。因此,本文主要讨论了这些参数对Δvew的影响,从而对共位卫星东西位置保持参数选择进行优化。

假设条件1：在±0.1°的定点窗口内,共位3颗面质比相同的卫星,偏心率摄动圆半径ρ=5.5×10-4,卫星偏心率矢量保持差值|Δe|=0.000 2。根据式(12)仅考虑二阶田谐项,可计算其中1颗卫星以不同保持周期在不同定点位置的Δvew,结果如图5所示。

由式(15)可知：平经度保持控制年度所需的速度冲量仅与定点位置平经度加速度相关。仅考虑二阶田谐项时,静止轨道卫星在不同定点位置平经度保持年度所需的速度冲量如图6所示。当卫星的定点位置确定时,平经度保持控制年度所需的速度冲量唯一确定,与保持周期无关。比较图5、6可发现：当周期不长(如图5中T=7,14 d)时,东西位置保持所需速度冲量为平经度保持所需速度冲量;当周期变长时,东西位置保持所需速度冲量在较大处的增幅较大。这主要是保持周期和定点位置平经度漂移率影响卫星偏心率矢量的结果。因此,研究东西位置保持的优化设置主要应考虑偏心率保持控制。

图5 不同定点位置和东西位置保持周期的年度速度消耗Fig.5 Δv for different longitudes with different EWSK durations

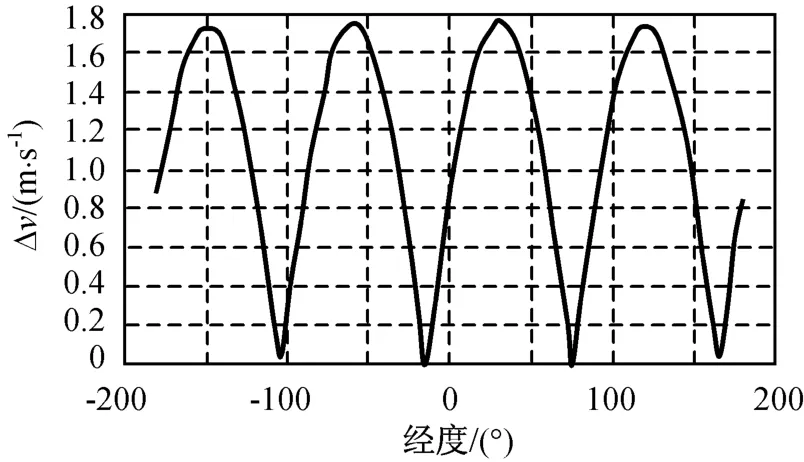
图6 不同定点位置平经度保持年度所需的速度冲量Fig.6 Δv for different longitudes with different cycle longitude keeping durations

根据式(16),偏心率保持控制所需的速度冲量主要与控制周期和偏心率控制圆半径两个参数相关。当T确定时,偏心率控制圆半径ec越大,卫星在1年中用于偏心率控制的速度冲量就越小。

偏心率引起卫星经度日周期性东西漂移幅度为2e。为保证卫星不超出东西保持窗口,当东西位置保持T确定时,要求将所有共位星群中卫星的偏心率矢量限制在一个半径为emax偏心率保持圆内,即

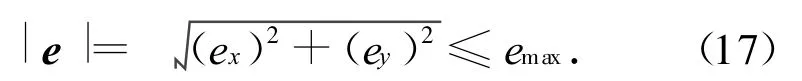
由式(9),偏心率控制圆的半径ec满足

式中：ex,ey分别为偏心率矢量在x、y轴的分量。

由此可知：ec的取值范围为。当偏心率限制圆半径emax确定时,共位星群中增大各卫星的偏心率控制半径,必然会减小各卫星的偏心率控制圆圆心距,使卫星相对距离减小(不考虑倾角隔离的影响)。

假设条件2：共位3颗面质比相同的卫星偏心率摄动圆半径ρ=5.5×10-4,在定点窗口东经116°±0.1°(=-0.001 99(°)/d2)内实施共位。以T=21 d为例,计算其中一颗卫星东西位置保持所需的年速度消耗和共位卫星偏心率产生的最小间隔与偏心率控制圆半径的关系以及与偏心率矢量差产生最小间隔的关系,结果分别如图7、8所示。为使卫星不超出东西位置保持窗口,并满足21 d进行1次偏心率控制的条件,共位星群中各卫星的控制圆取值范围均为[9.88×10-5,3.94×10-4]。

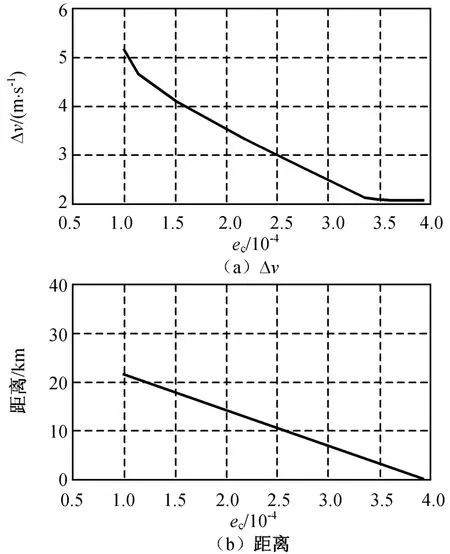
图7 不同偏心率控制圆半径的年速度消耗和卫星最小间隔Fig.7 Δv and minimum distance of satellites with different radii of eccentricity control circle

由图7可知：增大卫星的偏心率控制圆半径降低卫星能量消耗的同时也使共位卫星间偏心率产生的最小相对距离减小。当各卫星偏心率控制圆半径大于一临界值ecc时(图7中ecc=3.5×10-4),由于平经度保持所需速度冲量大于偏心率控制所需速度冲量,则年度速度消耗主要为平经度保持所需速度消耗,继续增大偏心率控制圆半径也不会减少能量的消耗,但共位卫星间最小距离仍会逐渐减小。

图8 不同偏心率矢量差的年速度消耗和卫星最小间隔Fig.8 Δv and minimum distanceof satellites with differentΔe

当emax确定时,共位卫星间的偏心率矢量差|Δe|的大小和卫星的偏心率控制圆半径密切相关,对年速度消耗和卫星最小间隔的影响与偏心率控制圆半径的影响相反。|Δe|也存在一临界值|Δe|c(图8中|Δe|c=0.9×10-4),当|Δe|≤|Δe|c时年度速度消耗主要为平经度保持所需速度消耗。

实时多星共位任务时,为保证卫星之间存在一定的安全距离,需满足星群中各卫星间的|Δe|大于一个允许的最小值Δemin,即

因此,当控制周期和偏心率摄动圆半径确定时,为减小共位卫星东西位置保持的能量消耗,应在式(17)、(19)的约束下,使共位星群中卫星的ec尽可能大,直至临界值ecc。

根据式(16),卫星T变化时对其能量消耗产生直接影响。由式(1)、(4)可得T的变化和偏心率限制圆半径满足关系

在某一定点位置,增大卫星的保持周期,会使共位星群的偏心率限制圆半径emax减小。若欲保持ec不变,则需减小|Δe|,减小卫星间的最小距离(不考虑倾角隔离的影响);若欲保持卫星间的|Δe|不变,则需相应减小卫星的ec,从而对卫星东西位置保持所需能量产生影响。

根据假设条件2,为保证卫星间存在一定的最小距离,设置卫星偏心率控制圆圆心距|Δe|=0.000 2(卫星间由此产生的隔离约8.4 km),各卫星的偏心率控制圆半径选择允许范围内的最大值。计算一颗卫星东西位置保持周期与最低年度速度消耗的关系,结果如图9所示。由图可知：当东西位置保持周期小于一临界值Tc时(图9中Tc=19 d),偏心率限制圆较大,平经度保持所需速度冲量大于偏心率控制,年度速度消耗主要是平经度保持所需速度消耗(图9中约为2.06 m/s);当周期大于Tc时,平经度保持所需速度冲量小于偏心率控制所需速度冲量,年度速度消耗主要体现为偏心率控制所需速度消耗,最低年度速度消耗随东西位置保持周期的增大而开始快速增大。

图9 不同东西位置保持周期的最低年度速度消耗Fig.9 Δv minimum for different EWSK durations

从能量最省的角度考虑,应选择东西位置保持周期T≤Tc,可使卫星东西位置保持所需能量最小。为便于测控任务的实施,常将保持周期设置为7 d的整倍数,如7,14 d。若为减少卫星生命周期测控任务的工作量,并考虑能量的消耗最小,则应选择T=Tc。

b)由式(15)、(16),将Tc作为保持周期在上述条件下计算各卫星的偏心率控制圆半径的临界值ecc,在能量消耗最小的情况下使偏心率矢量差最大。

用上述方法,根据假设条件2,可算得Tc=19 d,ecc=3.438 6×10-4,由ecc,|Δe|的关系可得|Δe|=2.372 6×10-4(卫星间由此产生的隔离约10 km),大于Δemin=0.000 2。

该方法在满足卫星隔离条件的前提下,考虑了减少测控实施的次数,并使卫星东西位置保持所需能量最小。但当卫星面质比较高(即卫星偏心率摄动圆半径较大)或位置保持半宽较窄时,无法获得Tc。

同样在定点窗口东经116°±0.1°内实施共位,计算不同偏心率摄动圆半径时的Δvew和不同平经度保持环半宽的Δvew分别如图10、11所示。由图10可知：当ρ增大时,Δvew有较大提高。当ρ=11×10-4时,对不同的东西保持周期,其偏心率保持所需速度冲量Δve均大于平经度保持所需速度冲量Δvl,Δvew主要为Δve并随ρ的增大而增大。由图11可知：当位置保持半宽Δλs减小时,Δvew有较大提高,且当Δλs小于某一值,对不同的东西保持周期,Δvew主要是Δve并随Δλs减小而增大。这时,只有根据实际情况尽可能采用较短的T,并设置共位星群卫星间偏心率矢量差为Δemin,才能使所需Δvew较小。

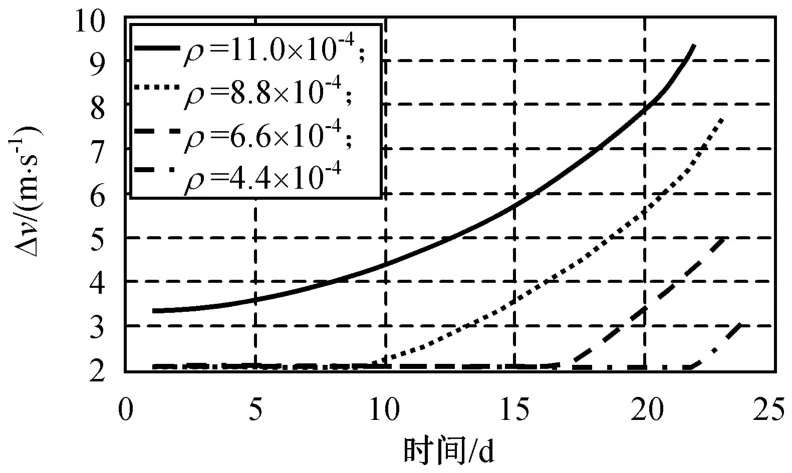
图10 不同偏心率摄动圆半径时东西位置保持周期的年度速度消耗Fig.10 Δv f or different EWSK durations with dif ferent radii of eccentricity control circle

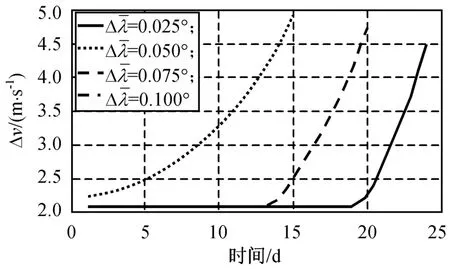
图11 不同平经度保持环半宽时东西位置保持周期的年度速度消耗Fig.11 Δv minimum for dif ferent EWSK durations with differentΔλ

4 结束语

本文通过对共位卫星东西保持参数对其能量消耗影响的分析,提出了一种共位卫星保持的优化方法。该方法在满足卫星隔离条件的前提下,考虑了减少测控实施的次数,并使卫星东西位置保持所需能量最小。采用此方法,不但利于静止轨道多星共位任务的规划设计,而且可对单一静止轨道卫星的东西位置保持进行优化。

[1]SRINIVASAMURTHY K N.Strategy analysis for collocation of INSAT-2 satellites[J].Acta Astronautica,2002,50(6)：343-349.

[2]LEE B S.Analysis of a station-keeping maneuver strategy for collocation of three geostationary satellites[J].Control Engineering Practice,1999,30(7)：153-161.

[3]EMMA B P,PERNICKA H J.Algorithm for autonomous longitude and eccentricity control for geostationary spacecraft[J].J.Guidance Control Dynam,2003,26(3)：483-490.

[4]ROMERO P,GAMBI J M.Optimal control in the east/west station-keeping manoeuvres for geostationary satellites[J].Aerospace Science and Technology,2004(8)：729-734.

[5]SOOP E M.地球静止轨道手册[M].王正才(译).北京：国防工业出版社,1999年.

[6]章仁为.卫星轨道姿态动力学与控制[M].北京：北京航空航天大学出版社,1998.