夹芯的典型参数对夹层板受迫振动影响分析

卫洪涛,孔宪仁

(哈尔滨工业大学 卫星技术研究所,黑龙江 哈尔滨 150086)

0 引言

蜂窝夹层板因其高比硬度和比刚度在工业领域获得了广泛应用,尤其是航天器大量采用蜂窝夹层结构用于外壳面板、承载结构,研究蜂窝夹层结构的振动响应对研究整个航天器的动力学响应意义重大。对蜂窝板自由振动的研究获得了大量成果,由不同假设前提可建立不同的位移场,进而通过虚位移原理和变分方法得到夹层板的运动方程以预测蜂窝夹层板自由振动[1]。研究多针对蜂窝板的自由振动进行建模分析[2、3]。文献[2]用一阶和高阶剪切理论,通过汉密尔顿方程推导了四边简支蜂窝夹层板的自由振动运动方程,假设解为纳维解的简化形式,代入运动方程,用解得的代数方程组得到夹层板的低阶基频,另还研究了蜂窝胞元构造、夹心层高度及蜂窝胞元大小对蜂窝夹层板自由振动基频的影响。文献[3]用汉密尔顿方法推导了一阶剪切理论蜂窝夹层板的自由振动运动方程,用类似文献[2]的方法求解夹层板基频,讨论了经典理论和一阶剪切理论模型在求解蜂窝板不同阶次振动频率时的差别,以及蜂窝芯剪切模量和蜂窝夹芯密度对蜂窝板低阶频率的影响。本文从受迫振动角度分析了蜂窝夹层板受迫振动响应,比较了经典假设和一阶剪切理论两种方法的计算结果,用一阶剪切理论运动方程研究了蜂窝夹芯层泊松比对整板振动响应的影响。

1 位移场定义

采用经典板假设和一阶剪切理论研究夹层板的受迫振动,蜂窝夹层板的坐标系如图1、2所示。图中：h为蜂窝夹芯的沿y向的壁板边长;θ为蜂窝夹芯倾斜壁板与ox轴的夹角;t为蜂窝夹芯胞元的壁板厚度;l为蜂窝夹芯胞元的倾斜壁板边长。

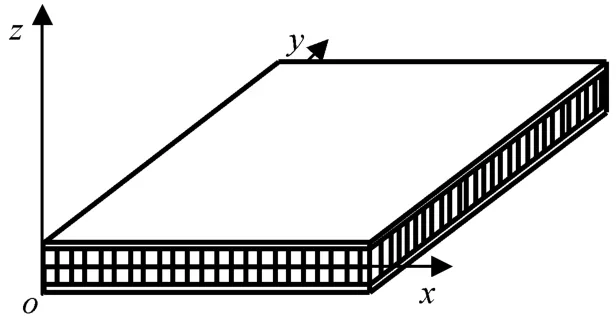
图1 蜂窝夹层板坐标系Fig.1 Coordinate of sandwich panel

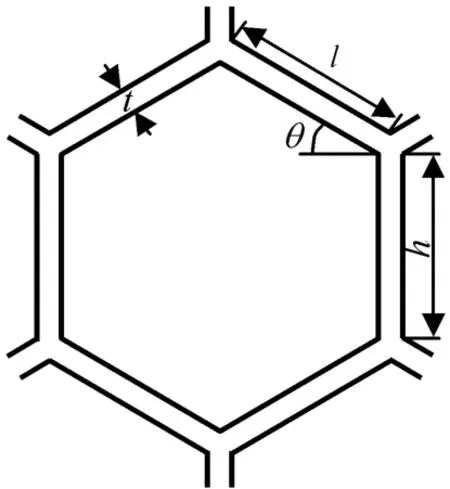
图2 蜂窝夹芯胞元示意Fig.2 Cell of honeycomb core

经典板假设位移场可表示为

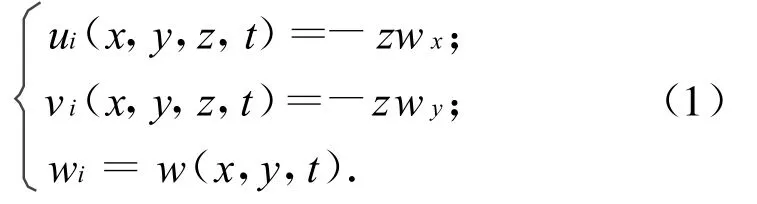
式中：ui,vi,wi分别为蜂窝夹层板各层任意点x、y、z向的位移;x,y,z为坐标。此处：i=1,2,3。

一阶剪切理论夹层板位移场可表示为

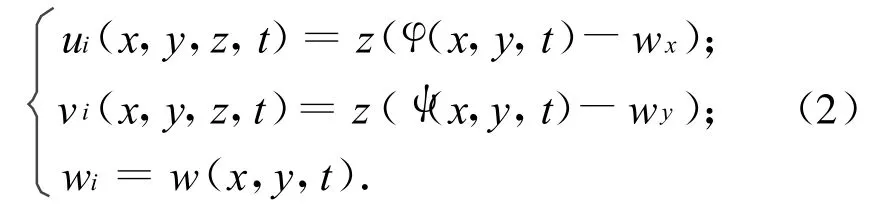
式中：φ(x,y,t),ψ(x,y,t)分别为平面xoz、yoz内夹层板中面垂线弯曲后的角度。

2 夹层板运动方程

由虚位移原理,对整个夹层板可得

式中：σix,σiy,σixy,σixz,σiyz为 蜂窝夹层板各层应力;εix,εiy,εixy,γixz,γiyz为蜂窝板各层应力对应的应变;ρi为蜂窝夹层板各层的密度;q(x,y,t)为蜂窝夹层板面板所受的均布载荷;δ为变分符号。将式(3)代入位移场,经变分运算并在z向积分得运动方程为

a)经典板假设

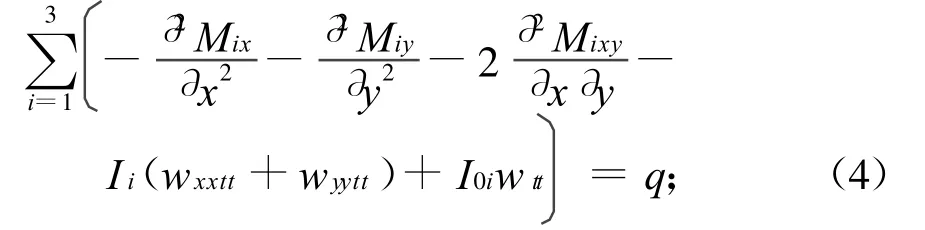
b)一阶剪切理论

式中：Qixz,Qiyz分别为蜂窝夹层结构各层在平面xoz、yoz的剪切力;σix=[Ei/(1-(μi)2)](εix+μiεiy);σiy=[Ei/(1-(μi)2)](εiy+μiεix);σixy=[Ei/(2+μi)]γixy;Mij为蜂窝夹层板各层力矩,且Mij=,Ii,分别为各层密度及其与z2乘积在各层内z向的积分,且。此处：Ei,μi分别为蜂窝夹层板各层的弹性模量和泊松比;j=x,y,xy。

3 数值仿真及典型算例

工程上关注的低阶振动频率可用伽辽金方法近似获得。对四边简支的蜂窝夹层板,满足边界条件的近似解为

a)经典板假设

b)一阶剪切理论

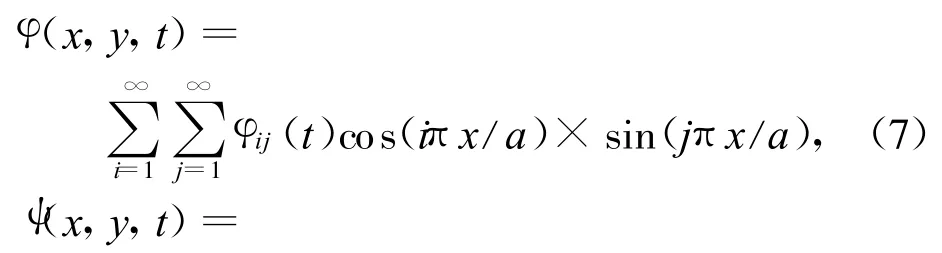
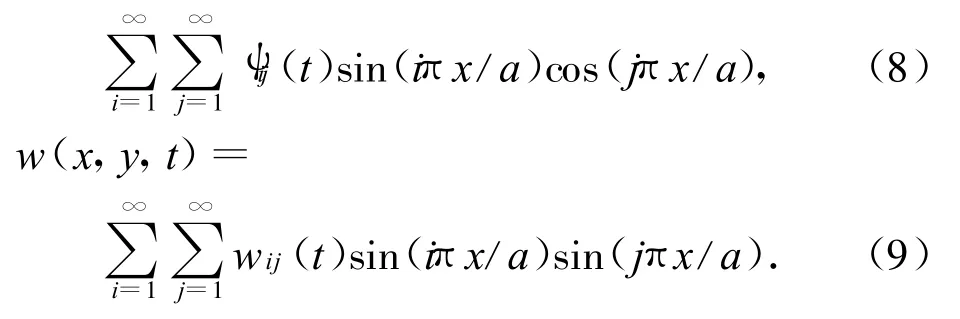
式中：a为蜂窝夹层板长。令i=j=1,即得低阶的振动频率。运用伽辽金方法的步骤为：

a)将应力-应变关系代入运动方程,蜂窝夹芯层弹性模量取文献[2]数值;

b)将满足边界条件的解代入运动方程,同时在式(5)的3个分式两边分别乘cos(πx/a)sin(πx/b),sin(πx/a)cos(πx/b),sin(πx/a)sin(πx/b)(经典板假设理论乘sin(πx/a)sin(πx/b));

c)在整个板面进行面积分,得由φ(t),ψ(t),w(t)表示的偏微分方程(经典板假设理论是用w(t)表示的一个等式)。

这样可得有3个未知数的偏微分方程组,本文用Matlab/Simulink软件求数值仿真解。步骤为：

a)建立Simulink模型,偏微分方程组的未知数为φ(t),ψ(t),w(t);

b)选择一适当的外加载荷幅值及仿真外加激励力的频率范围;

c)用Matalb软件中的m文件控制Simulink仿真,根据所选的幅值在选择的频率范围内进行批量仿真;

d)返回步骤b),改变外加载荷幅值,重复步骤b)、c)可得蜂窝夹层板不同外加载荷幅值的幅频响应图。

设典型铝蜂窝夹芯板的面板及正六边形蜂窝芯的材料均为铝,各参数为：a=1 m,宽b=1 m,铝密度ρ=2 780 kg/m3,芯层厚度hc=24.4 mm,面板层厚度d=0.3 mm,面板弹性模量E s=70 GPa,l=4 mm,t=0.04 mm。比较经典理论与一阶理论间的差异,并用一阶理论研究泊松比对振动频率的影响。

为便于比较,令芯层厚度为0,改变面板层厚度,比较两种方法。令hc=0 mm,在d分别为0.1,0.2 mm(其他参数不变)条件下,两种板假设理论获得的夹层板幅频响应如图3、4所示。由图可得夹层板的一阶基频。

比较发现：经典理论和一阶剪切理论所得的蜂窝夹层板基频相差10-1Hz量级,表明一阶剪切理论模型可靠。

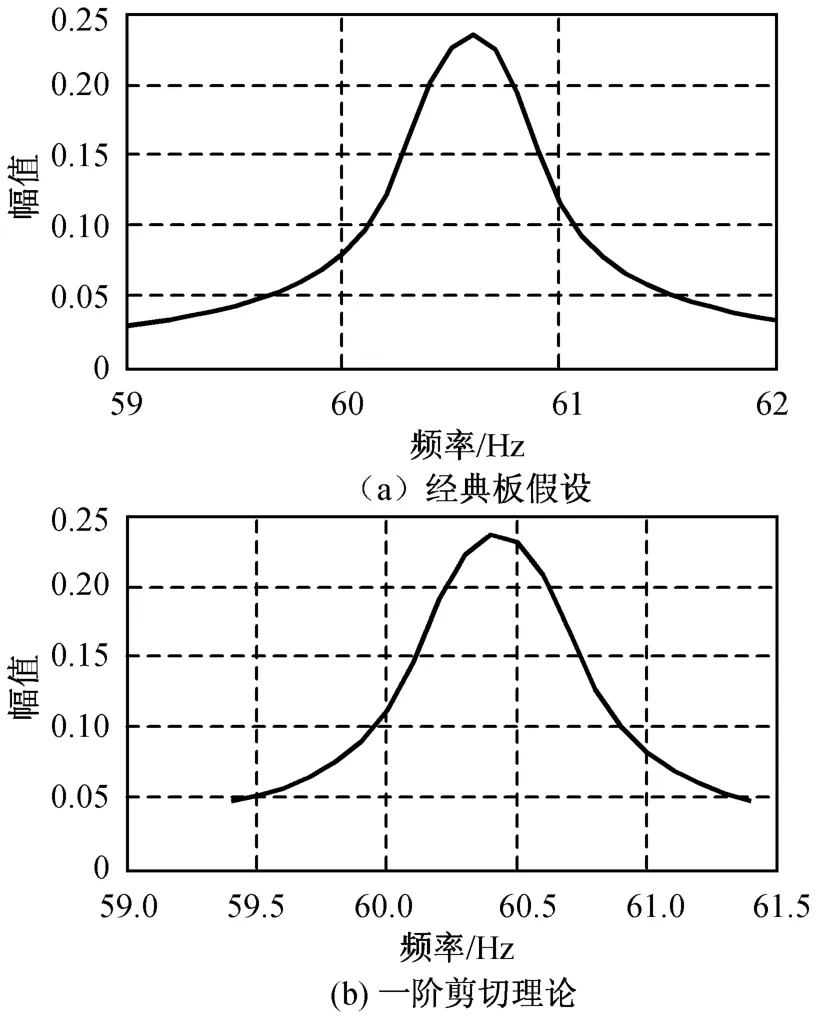
图3 d=0.1 mm时仿真结果Fig.3 Simulation results of a classical plate theory and low order shear deformation when d=0.1 mm

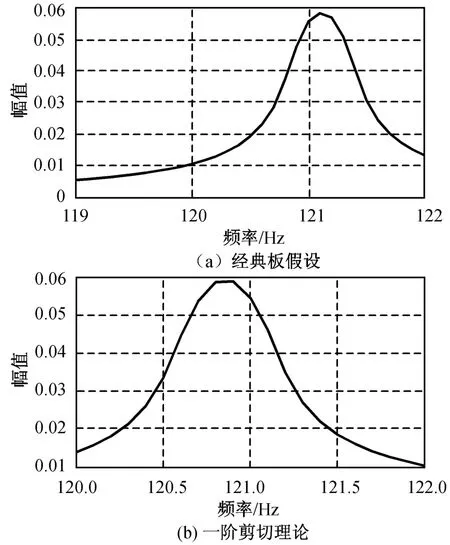
图4 d=0.2 mm时仿真结果Fig.4 Simulation results of a classical plate theory and low order shear deformation when d=0.2 mm

4 蜂窝夹芯泊松比对整板振动的影响

单独的蜂窝夹芯层的静态力学研究可得泊松比较大的结论[4、5]。部分文献在用数值方法研究蜂窝夹层板的振动响应时,均采用工程数值0.3。本文基于一阶剪切理论模型,讨论蜂窝夹芯的泊松比对动力学响应的影响。设蜂窝板参数不变,hc=10 mm,d=0.3 mm,泊松比从0.2增至1.0,步长0.1,仿真所得不同泊松比的一阶频率响应见表1,幅频响应如图5所示。由图中共振峰位置可得不同蜂窝夹层泊松比的蜂窝夹层板一阶频率。

由仿真结果可知：当蜂窝夹芯泊松比为0.1～0.9时,对结果的影响较小;当泊松比为0.9～0.999 9…时,响应结果间的差异明显增大,尤其是当泊松比为0.999～0.999 9…时,夹芯弯矩急剧增加,显著改变了响应。根据该算例,泊松比为0.999 9,0.9间的差异可达19.3%。

表1 不同蜂窝夹芯泊松比的一阶频率响应Tab.1 Low order natural frequency with various Poisson ratio

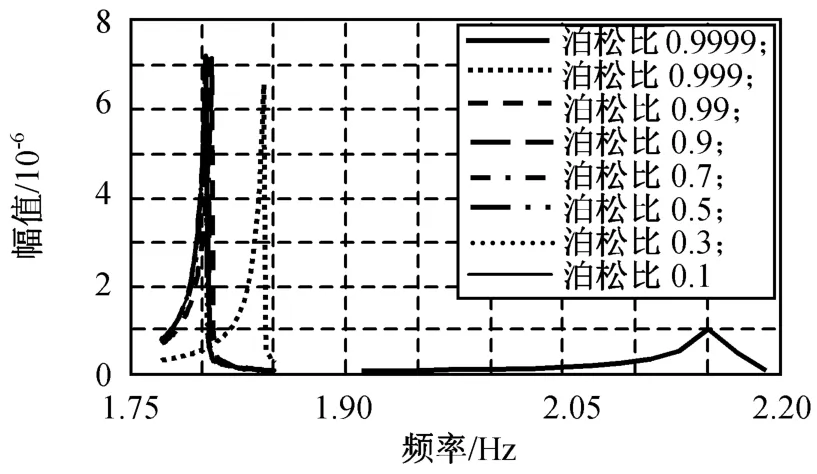
图5 选择不同蜂窝夹芯层泊松比蜂窝板的幅频响应Fig.5 Amplitude under frequency of a specific honeycomb coresandwich panel with dif ferent Poisson ratio

5 结束语

本文对蜂窝夹层板受迫振动进行了研究。比较了经典假设和一阶剪切理论的计算结果。分析表明后者可行。基于理论模型,讨论了研究蜂窝夹芯的泊松比对响应结果的影响,发现泊松比在接近1时对响应有显著的影响。研究对蜂窝夹层板的非线性振动响应和工程应用有一定的参考价值。

[1]IRVING H.Energy and finite element methods in structural mechanics[M].Washington：Hemisphere Pub,1996.

[2]LIU Q L,ZHAO Y.Effect of soft honeycomb core on flexural vibration of sandwich panel using low order and high order shear deformation models[J].Journal of Sandwich Structures and Materials,2007(9)：95.

[3]LIU Q L,ZHAO Y.Prediction of natural f requencies of a sandwich panel using thick plate theory[J].Journal of Sandwich Structures and Materials,2001(3)：289.

[4]GIBSON L J.The mechanics of two-dimensional cellular materials[J].Proc R Soc Lond,1982.

[5]祝 涛,王德禹.蜂窝芯层非线性等效弹性参数[J].上海航天,2008,25(4)：51-54.