碳纤维支架振动抑制方法研究

曹 亮,雷勇军,申智春

(1.国防科学技术大学 航天与材料工程学院,湖南 长沙 410073;2.上海卫星工程研究所,上海 200240)

0 引言

某卫星的碳纤维支架顶部安装了卫星重要有效载荷,底部通过过渡板安装在仪器板上,类似悬臂结构。该载荷支架受整星布局和质量特性的约束,其安装位置和3根撑杆形成的张角受限制。小撑杆用M 55J/环氧复合材料缠绕成型,上下支座采用铝合金LY12材料,加强板采用M55J/环氧复合材料层合板。设计中,其载荷响应是重点和关键。在整星振动试验中,曾发生过响应超标。为此,在支架撑杆上粘贴了约束阻尼层,在之后的整星振动试验中响应下降了23%[1]。为在新批次卫星研制中避免类似问题,本文对该卫星支架的振动抑制方法进行了研究。

1 碳纤维支架有限元模型

支架结构主要由上下支座、小撑杆组件和加强板等组成,如图1所示。有限元分析采用MSC.Patran/Nastran软件。在有限元模型中,上下支座用实体单元建模,小撑杆组件和加强板均用壳单元建模。不考虑约束阻尼层单元数量,共建立实体单元4 214个,壳体单元8 288个。其中：约束阻尼层结构分析一般采用板-实体-板方法建模,约束阻尼层粘贴在小撑杆组件上,可用该模型进行修改;撑杆内部填充减振材料时,用实体单元对聚氨酯材料建模,可在小撑杆内部直接建模;结构修改时,可直接修改支架结构有限元模型。三种模型统一,利于结果间的比较,不必考虑建模差异造成的误差。载荷结构部分采用载荷单位提供的模型,支架结构与载荷的连接直接用有限元中的RBE2刚性单元连接。

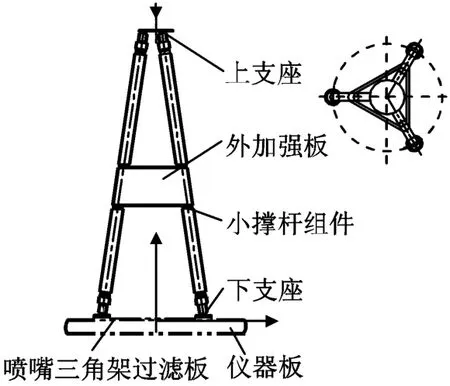
图1 碳纤维支架示意Fig.1 Carbon compositebracket

本文中支架结构的材料特性为：2A12T4材料,弹性模量E=70 GPa,泊松比ν=0.33,密度ρ=2 700 kg/m3;M 55J/环氧复合材料,0°,90°向弹性模量弹性模量E11=288 GPa,E22=9 GPa,ν=0.266,面内剪切模量G12=4.6 GPa,ρ=1 600 kg/m3;小撑杆的铺层为[±15°]6/90°。支架结构的主要几何属性为：下支座板厚4.5 mm,柱段连接高度30 mm;上支座板厚4.5 mm,柱段连接高度30 mm;小撑杆内径22 mm,外径25 mm,长734 mm;加强板壁厚1.2 mm,高100 mm。阻尼层选用Zn-1材料,厚1.5 mm,剪切模量1.56 MPa,ρ=1 100 kg/m3,阻尼层损耗因子1.13。

2 约束阻尼层修正方案

约束阻尼层结构通过阻尼层的剪切变形将机械振动的能量转为热能耗散,以有效减少谐振时的振动放大。对管状结构或曲面薄壳结构,整体约束层或阻尼层的减振效果一般并不理想,其结构损耗因子较小。若将约束层或阻尼层分隔开,能明显增大结构损耗因子,改善减振效果[2、3]。由文献[3]中的定义,用有限元仿真法分析了部分离散约束阻尼层、全部离散约束阻尼层,以及全约束离散阻尼层支架的模态与频响,并与原方案(全约束阻尼层)比较,结果见表1。其中：约束层1以M55J/环氧复合材料编制布为约束层,约束层2以T300编织布为约束层材料,不同附加约束阻尼撑杆截面如图2所示。

由表1可知：全约束离散阻尼层的减振效果与全约束阻尼层相近;约束阻尼层的减振效果受约束层影响更大,用高模量的碳纤维作为约束层时约束阻尼的效果更好;对全约束阻尼层,用全约束离散阻尼层的附加质量更小,附加阻尼层质量仅略多于全约束阻尼层的50%,而全约束阻尼层的代价更小。因此,建议采用全约束离散阻尼层方案。

3 结构修改(加强板)改进方案

碳纤维支架受限于整星布局,整体结构不能有较大改变。但加强板能增大结构的抗弯刚度,增加固有频率,另外加强板的覆盖面积增大会增加结构质量,对板质量有一定限制。因此,改变加强板结构能改变支架刚度和固有频率,并不影响整星的布局,且改变加强板可不用修改模具,代价最小。

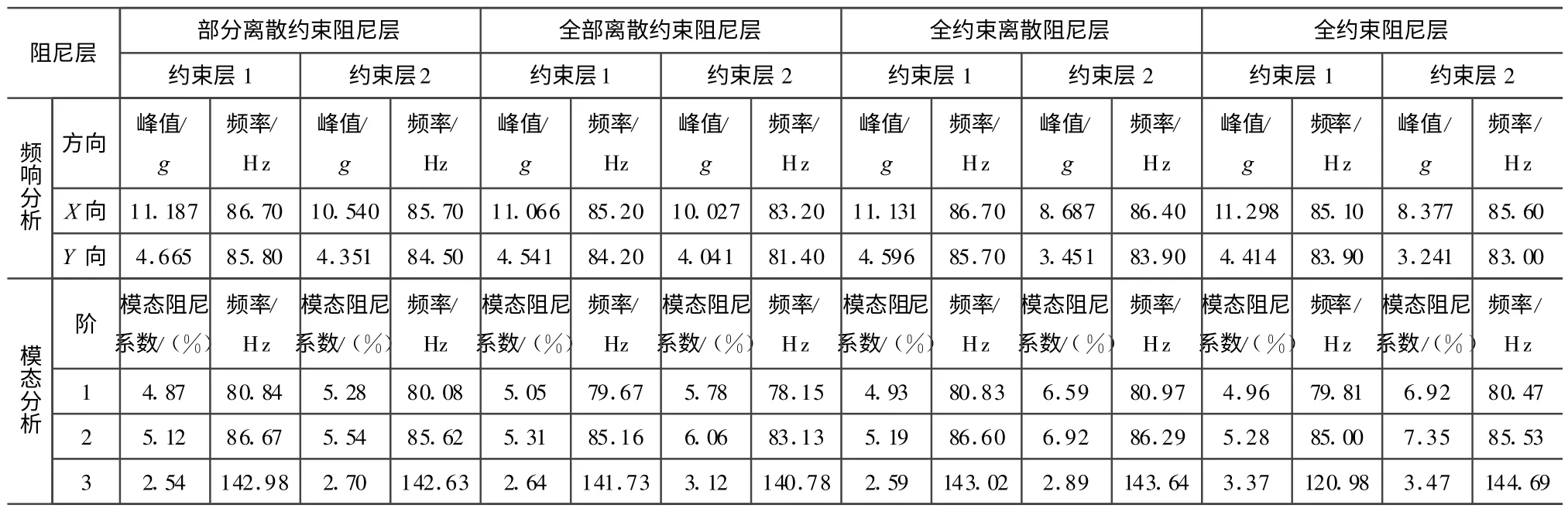
表1 不同约束阻尼层结构的结构模态与频响分析结果Tab.1 Analysis results of structure modal and frequency response for various layer structure constrained damping

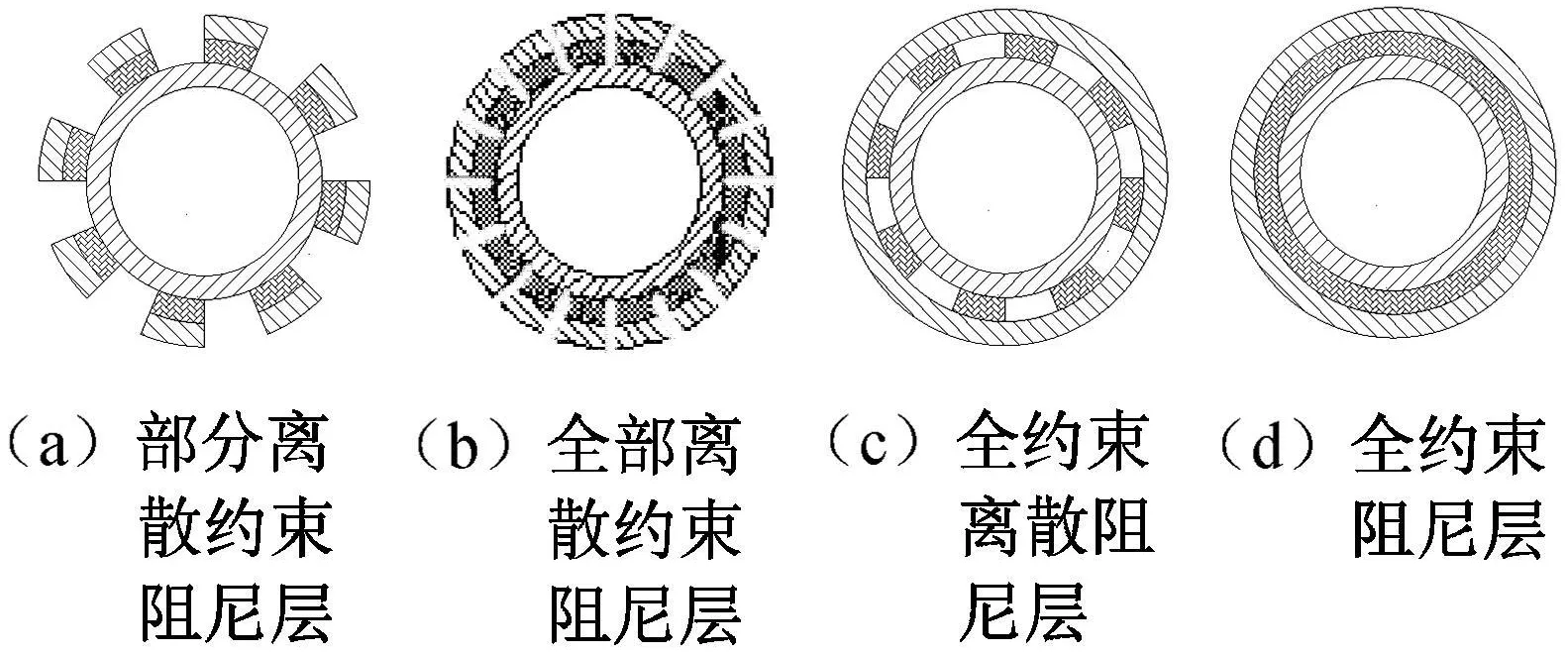
图2 不同附加约束阻尼撑杆截面Fig.2 Section of strut with additional constrained damping

用有限元分析方法分析了不同工况的加强板结构对该支架组件动力学特性的影响,结果见表2。其中：工况1为无阻尼三角架去加强板;工况2为原方案;工况3为原始碳板基础加装碳板1圈;工况4为全包围碳板(厚度不变);工况5为全包围碳板,外碳板厚度减半。各工况结构如图3所示。表2中：频响与模态分析均在支架组件基础上分析;上标*为响应峰值频率对应模态。

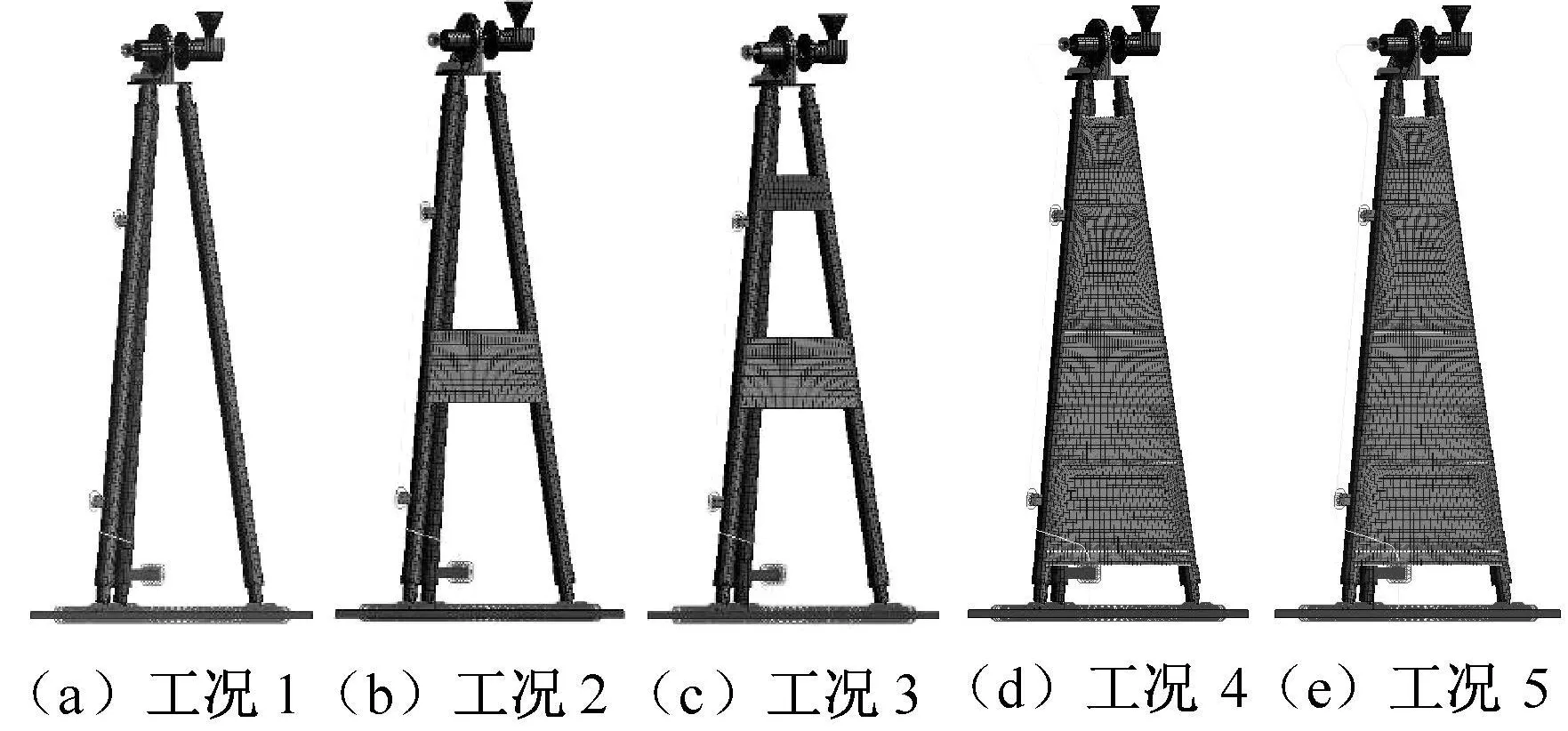
图3 不同附加约束阻尼撑杆截面Fig.3 Section of strut with various constrained damping

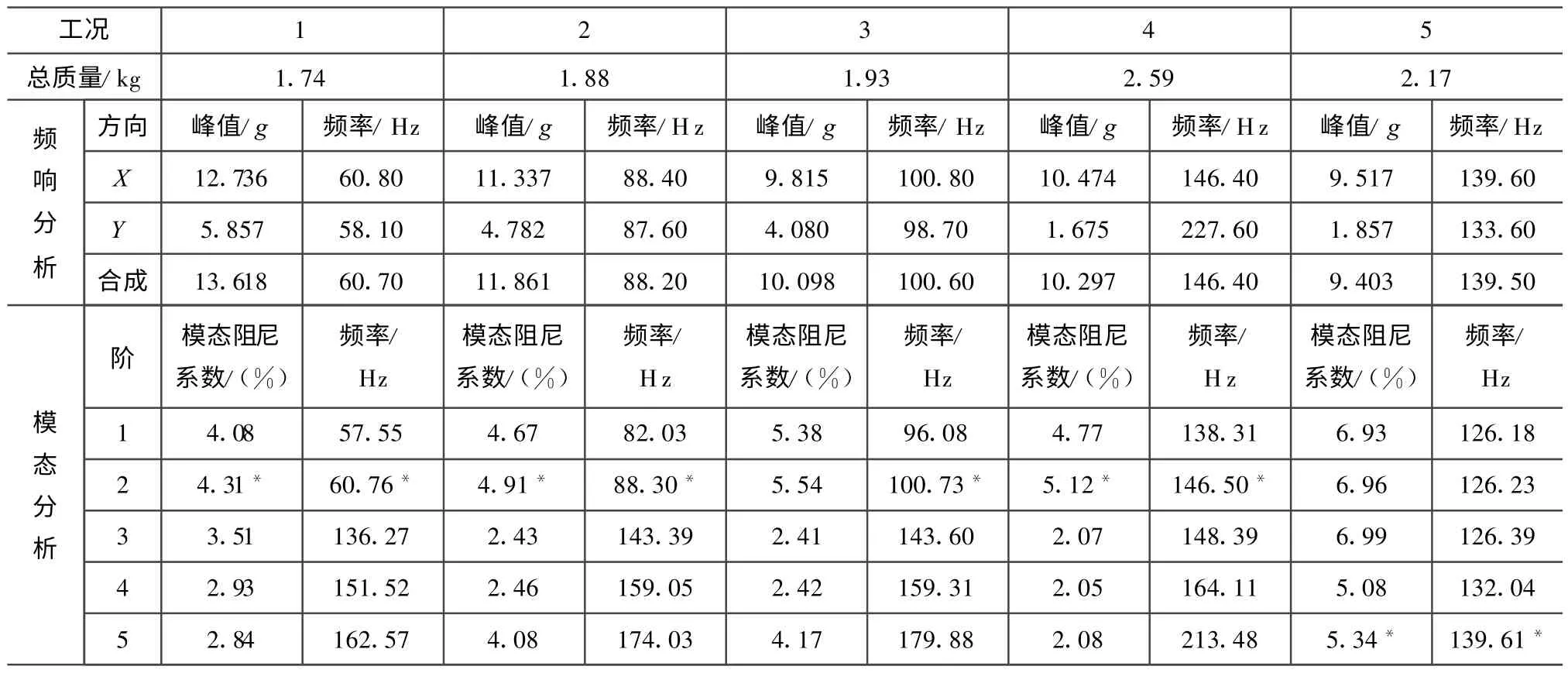
表2 不同加强碳板结构的结构模态与频率响应分析结果Tab.2 Analysis results of structure modal and frequency response for various reinforcing plate structure of constrained damping

由模态分析结果可知：当加强板厚不变时,响应峰值频率对应第二阶模态;外加强板厚度减半后,板的刚度显著减小,使模态分析结果中的前三阶模态为外加强板的局部模态,实际支架顶端响应峰值频率对应第五阶模态。模态阻尼系数会改变,二阶模态阻尼系数随外加强板覆盖面积变大而先增大后减小,最大值出现在工况3,最小值出现在工况1,分别为5.54×10-2,4.31×10-2,前者较后者增加1.23%。工况4、5仅外加强板厚度不同,频响峰值频率对应的模态阻尼系数分别为5.12×10-2(第二阶模态),5.34×10-2(第五阶模态),工况5较工况4增加0.22%,说明此时碳板厚度减半可增大结构的模态阻尼系数。

由频率响应结果可知：当加强板厚不变时,工况1主振方向响应峰值最大,工况3主振方向响应峰值最小,分别为12.736g,9.815g,相差2.921g,相当最大峰值的23.52%,表明采用工况3中的加强板结构时主振方向响应峰值明显下降;同样加强板厚不变时,工况4响应峰值对应的频率最大,工况1响应峰值的频率最小,分别为146.40,60.80 Hz,相差为85.6 Hz,约为工况1响应峰值对应频率的1.4倍,这可使支架的基频与卫星耦合频率的差值增大,非常利于避免卫星仪器安装板与支架间的振动耦合,进而也会实现减振(增大加强板的覆盖面积可减小响应峰值,同时亦可明显增大响应频率)。当加强板厚改变时,工况5支架结构(加强板厚度减半)的加强板质量和刚度均小于工况4,其响应峰值频率为139.60 Hz,较工况4减小6.80 Hz,但仍较工况1增大约80 Hz;工况5的主振方向响应峰值为9.517g,较工况4减小0.957g,下降9.14%。可见外加强板厚度减半对支架响应峰值影响明显,但对响应峰值频率的影响较小。工况5的主振方向响应峰值在5个工况中最小,较工况1(主振方向响应峰值最大)减小3.219g,下降25.27%。

综上,加强板对支架结构的基频影响显著,同时可减小支架顶部响应峰值。采用全覆盖半厚度加强板结构(工况5),支架即可获得较好的减振效果,且对结构质量影响较小,与原方案相比,其主振方向响应峰值降低较显著,而改动最小且最易实现的是工况3。

4 支架撑杆内部填充减振材料

碳纤维材料的网球拍为加强减振性能,在内部填充热塑性聚氨酯之类的泡沫材料,此类结构多为圆形空心结构,与支架撑杆结构相似。聚氨酯泡沫材料密度仅为0.1 g/cm3,多孔,且具黏弹性,是减振吸能的优质材料。考虑将硬质聚氨酯泡沫塑料材料填充到3根撑杆结构内部空心处,取ρ=0.6 g/cm3,ν=0.4。因聚氨酯的弹性模量和阻尼系数与材料制备配方及工艺有关,弹性模量和损耗因子随温度与频率会出现一定偏移,实际应用中两个参数取值范围较广且随环境影响而变[4]。

弹性模量在200～1 600 MPa间等距取8个值,阻尼系数在0.2～1.0间等距取5个值,分别对支架结构进行模态与频率响应分析获得结构整体的二阶模态阻尼系数(根据前文的分析,响应峰值频率对应为第二阶模态)以及结构在满振激励下的主振方向响应。结果发现各工况的响应曲线相似,其中弹性模量为1 600 MPa、损耗因子为1工况的响应分别如图4、5所示。

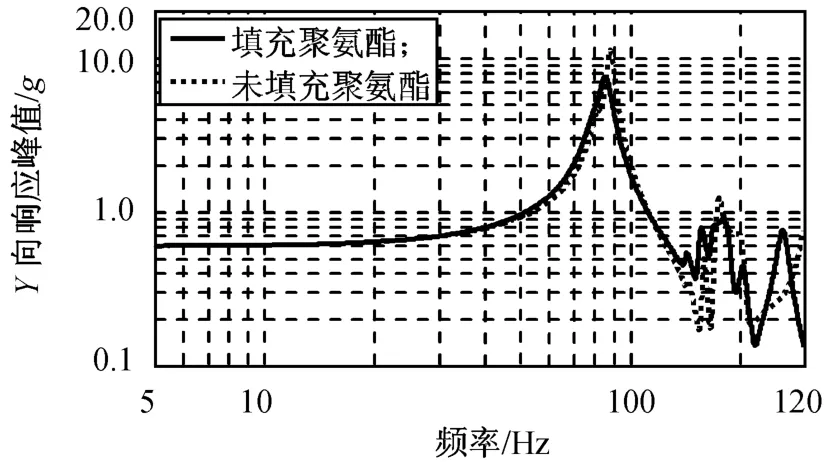
图4 填充聚氨酯三角架Y向满振激励主振方向响应Fig.4 Main vibration response of tripod filled with polyurethane in Y axis

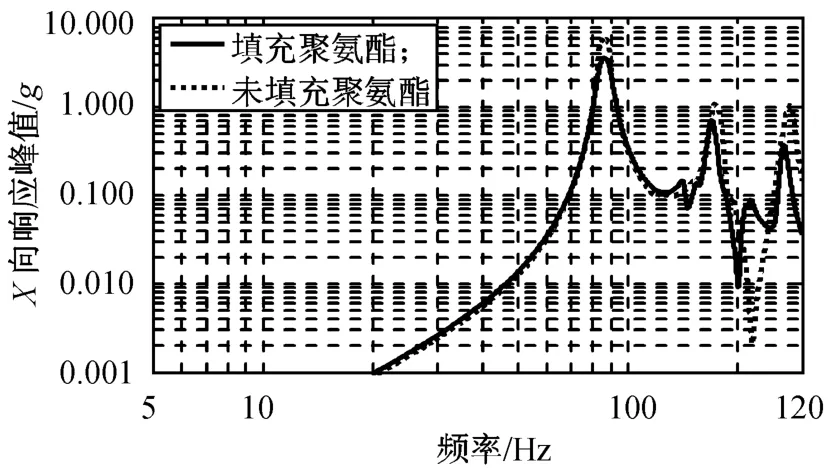
图5 填充聚氨酯三角架X向满振激励垂直方向响应Fig.5 Vertical vibration response of tripod filled with polyurethane in X axis

4.1 填充聚氨酯材料对模态阻尼的影响

在聚氨酯材料为不同弹性模量和损耗因子η的填充工况下,轴向推力器三角架结构的模态阻尼计算结果见表3。

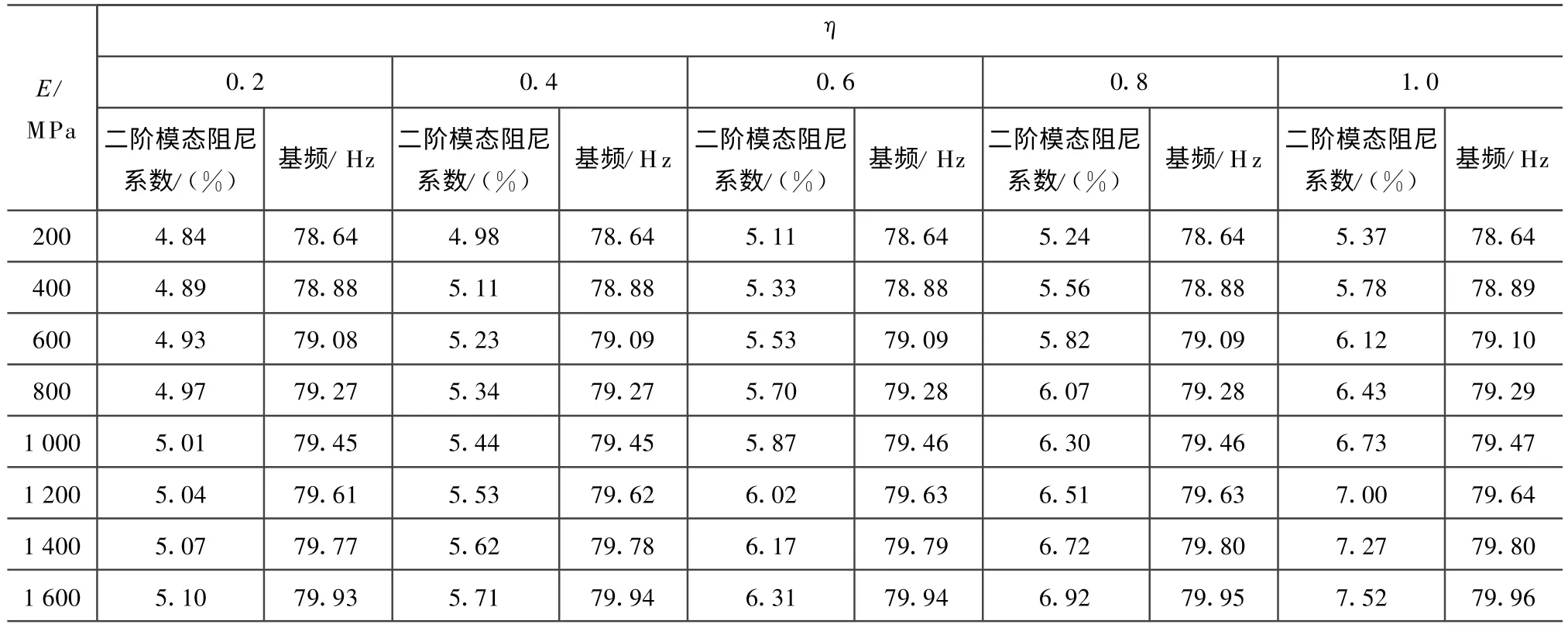
表3 不同弹性模量和材料损耗因子条件下结构模态分析结果Tab.3 Analysis result of structure modal with various elastic modulus and material loss factor

由表3可得不同弹性模量的二阶模态阻尼系数如图6所示。由图可知：模态的阻尼系数随弹性模量增大而变大,且曲线斜率随材料损耗因子增大而增加。类似可得不同材料损耗因子的二阶模态阻尼系数如图7所示。图中：曲线1～8的E分别为200,400,600,800,1 000,1 200,1 400,1 600 MPa。由图可知：模态阻尼系数亦随材料损耗因子增大而变大,且图中曲线变化规律趋于线性,且当弹性模量增大时,模态阻尼系数增大较平稳。比较最值可知：各工况中模态阻尼系数最小值为0.048,最大值为0.075,相差0.027(增大了56.52%)。

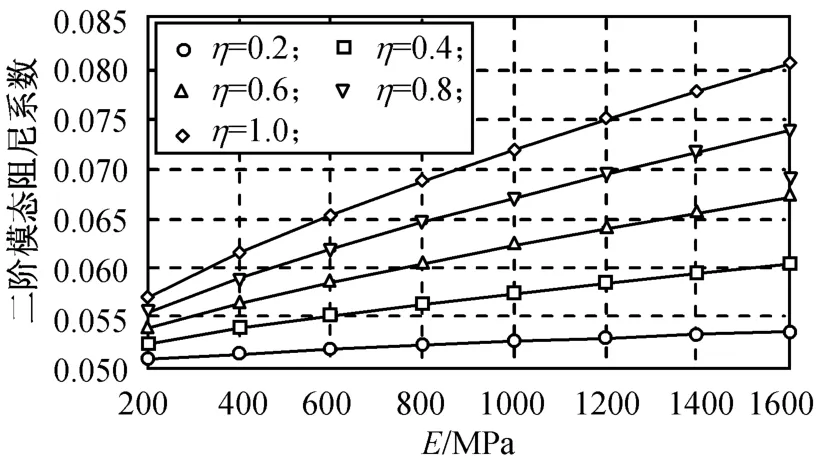
图6 不同弹性模量的模态阻尼系数Fig.6 Modal damping factor under various elastic modulus

由此可认为：增大聚氨酯材料的弹性模量和材料损耗因子利于增强结构的阻尼,当参数合适时,结构的二阶模态阻尼系数可明显增大。

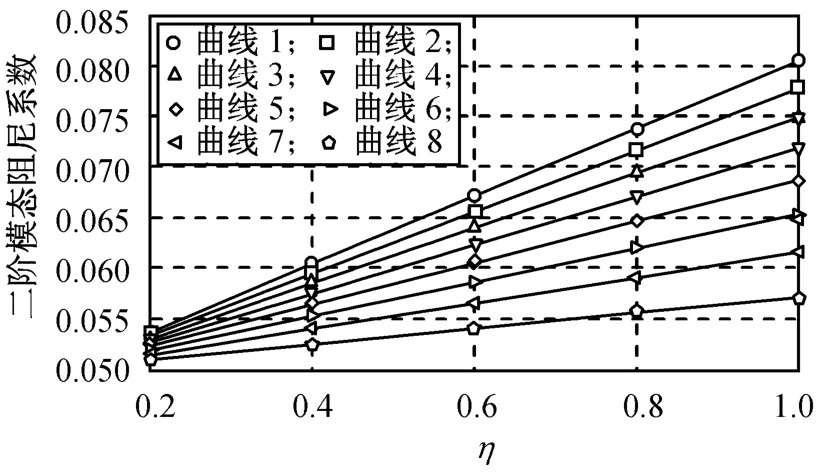
图7 不同材料损耗因子的模态阻尼系数Fig.7 Modal damping factor under various material loss factor

4.2 填充聚氨酯材料对响应峰值的影响

在聚氨酯材料为不同弹性模量和损耗因子工况下,主振方向频响峰值和对应的频率计算结果见表4。

由表4可得不同弹性模量的主振方向响应峰值如图8所示。由图可知：主振方向响应随聚氨酯材料弹性模量增大而减小,且减小趋势随材料损耗因子增大而更明显。同样可得不同材料损耗因子的主振方向响应峰值如图9所示。由图可知：主振方向响应亦随材料损耗因子增大而减小,且当弹性模量增大时主振方向响应增大较平稳。响应最小可为7.605g,较无阻尼层支架的11.337g减小3.732g(下降32.92%)。

由此可认为,增大聚氨酯材料的弹性模量和阻尼系数可明显减小结构响应。

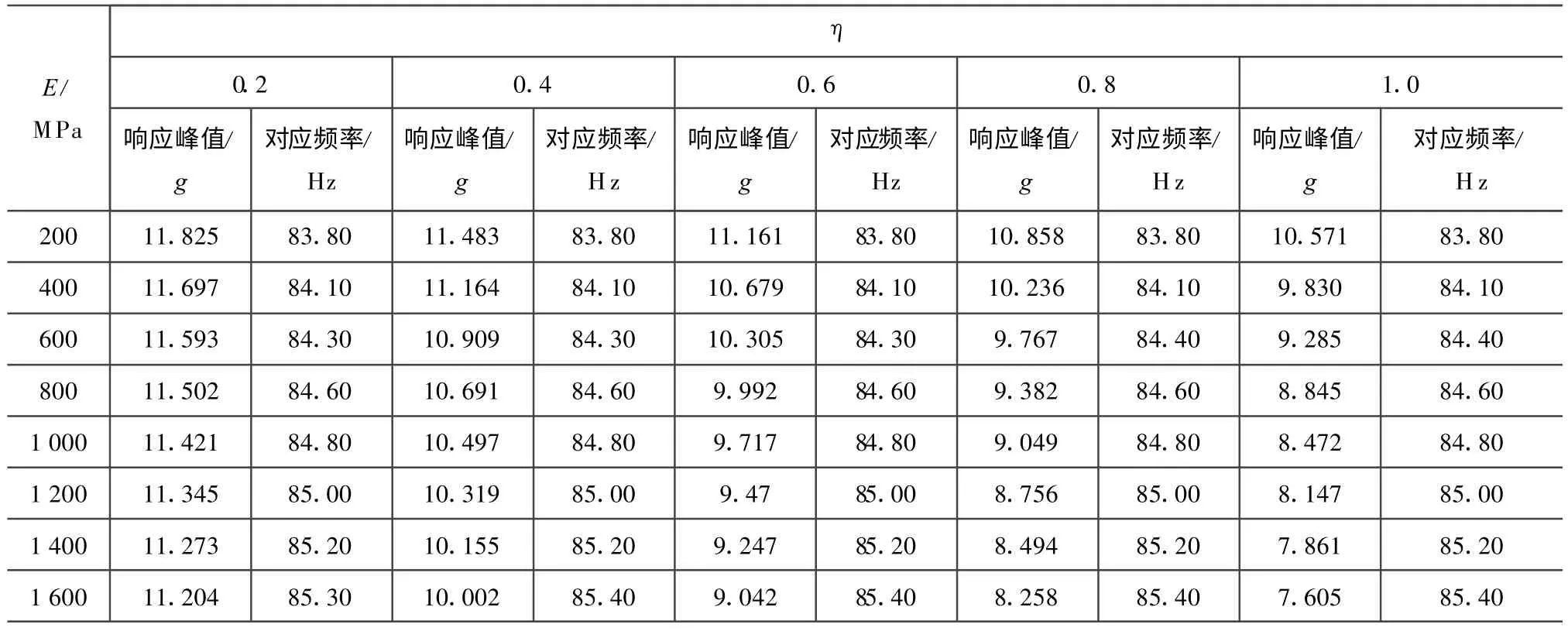
表4 不同弹性模量和材料损耗因子条件下结构主振方向频率响应分析结果Tab.4 Analysis result of frequency response in main vibration direction with various elastic modulus and material loss factor

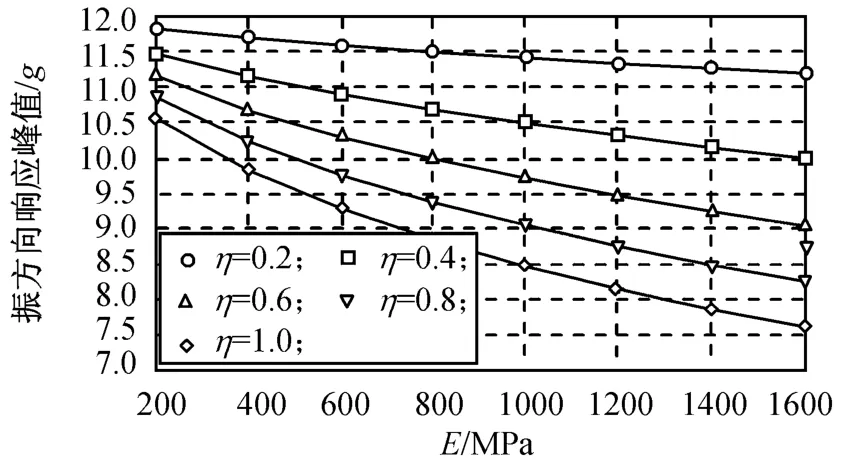
图8 不同弹性模量的主振方向响应Fig.8 Response in main vibration direction under various elastic modulus

填充聚氨酯泡沫塑料后质量增加0.554 kg,支架总质量为2.294 kg,与附加约束阻尼层后的支架质量2.240 kg相近,可认为支架整体质量在允许的范围内。

聚氨酯材料的力学性能可通过附加其他原料而大幅改善,如适量增加云母或玻璃纤维可使材料的弹性模量增加4倍多,附加片状石墨或云母等对材料的阻尼性能也有明显的促进作用,因此可通过优化配方使填充材料的耗能增大,减小结构响应峰值,从而实现进一步减振[4、5]。此外,高分子填充材料的种类多且新产品正不断出现,随着高弹性模量和损耗因子及低密度材料(如丙烯酸树脂泡沫)的研制成功,可能会有更适合的材料替代聚氨酯材料。

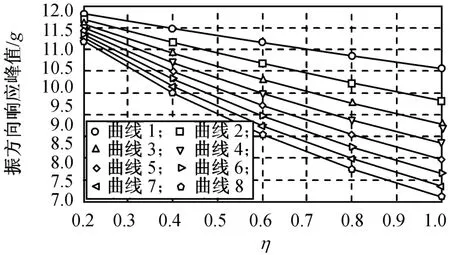
图9 不同材料损耗因子的主振方向响应Fig.9 Responsein main vibration direction under various material loss factor

5 方案比较

约束阻尼、加强板改进和支撑杆内部填充减振材料三种支架响应抑制方法的附加质量、工艺性、继承性和代价等的比较见表5。

表5 不同响应抑制方案比较Tab.5 Comparison of various schemes for response suppression

对约束阻尼方案,全约束阻尼方案已连续用于数颗卫星,振动试验效果较好。其中全约束离散阻尼层方案分析效果与全约束阻尼方案响应抑制效果相近,但工艺复杂性明显增大,且须避免约束层与基层的粘贴,以免影响阻尼效果,这加大了工艺难度,因此应选择全约束阻尼方案。加强板改进方案中工况3的代价最低,且不会引起星上如电缆走向等的变化。撑杆内部增加阻尼材料作为新的响应抑制方法,还有待卫星型号应用的探索。综合分析,本文认为该支架应在原约束阻尼方案的基础上,采用加强板改进方案中工况3,即增加加强板1圈。

6 结束语

本文对某卫星支架的响应抑制方法进行了研究,用有限元法分析了约束阻尼层、加强板修改和支撑杆内部填充减振材料三种改进方案对支架组件模态阻尼和频率响应的影响。综合考虑不同方案的优缺点,给出了该支架的设计改进方向,对该型卫星支架及星上类似结构的响应抑制有一定的参考意义。

[1]申智春,梁 鲁,郑钢铁.某星卫星有效载荷支架振动抑制[J].宇航学报.2006,27(3)：503-506.

[2]杜华军,陈恩鹏.航天结构的约束阻尼振动抑制优选方案研究[J].航天控制,2004,22(5)：8-11.

[3]戴德沛.阻尼技术的工程应用[M].北京：清华大学出版社,1991.

[4]厄特尔G.聚氨酯手册[M].阎家宾,吕槊贤(译校).北京：中国石化出版社,1992.

[5]王建华.聚氨酯阻尼材料研究进展[J].工程塑料应用,2002,30(10)：51-53.