(X，I)-Gorenstein内射模的可解性及等价刻画

何东林，李煜彦

(陇南师范高等专科学校数信学院，甘肃陇南742500)

Gorenstein同调理论是同调代数理论的研究热点之一。Holm[1]提出并研究了Gorenstein同调维数，Pan[2]等将其推广到(X，Y)-Gorenstein投射模与内射模，本文主要讨论(X，I)-Gorenstein内射模的可解性及其若干等价刻画。

本文中的环均指有单位元的结合环，模指左R-模，P表示投射左R-模类，I表示内射左R-模类。X,Y均为左R-模类，且I⊆X，P ⊆Y。HomR(X,-)表示所有函子HomR(X,-)组成的类，其中X∈X。先给出两个基本概念。

定义1[1]称模类X是内射可解的，如果I⊆X，且对任意短正合列

其中X′∈X，有X∈X与X″∈X等价。

定义2[2]称模M是(X，Y)-Gorenstein内射模，如果存在HomR(X,-)下正合的正合列其中M ≅Coker(Y1→Y0)且Yi,Yi⊆Y。

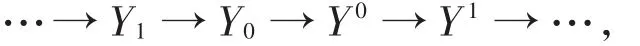
引理1如果模类Y关于直积封闭，那么(X，Y)-Gorenstein内射模也关于直积封闭。

特别地，当Y=I时，用(X，I)-GI表示所有(X，I)-Gorenstein内射模组成的类。显然内射模一定是(X，I)-Gorenstein内射模。下面给出本文的主要结论。

定理1设N是左R-模，则以下条件等价

(1)N是(X，I)-GI模；

(2)Exti≥1R(X,N)=0(对任意 X ∈X)，且存在HomR(X，-)下正合的正合列

…→I2→I1→I0→N→0，

其中Ii∈I(i=0,1,2,…)；

(3)存在短正合列0→K→I→N→0，其中I∈I且K ∈(X，I)-GI。

证明 由定义易知(1)⇔(2)⇒(3)显然成立。下面只需证(3)⇒(2)成立即可。

因为在短正合列0→K→I→N→0中K∈(X，I)-GI，所以对任意i≥1及任意X ∈X，有Exti

R(X,K)=0且存在HomR(X，-)下正合的正合列

其中Ii∈ I(i=0,1,2,…)。用函子HomR(X，-)作用于短正合列0→K→I→N→0可得如下长正合列

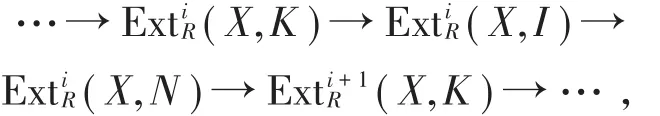
又由I∈I知

结合正合列…→I2→I1→I0→K→0及0→K→I→N→0易得HomR(X，-)下正合的正合列…→I2→I1→I0→I→N→0。

定理2 模类(X，I)-GI是内射可解的。

证明 设0→M→N→Q→0是左R-模短正合列，其中M ∈(X，I)-GI。若Q ∈(X，I)-GI，因为内射模类I关于直积封闭，由引理知模类Q∈(X，I)-GI也关于直积封闭。根据文献[1]中引理1.7可得，模类(X，I)-GI关于扩张封闭，从而N ∈(X，I)-GI。若N ∈(X，I)-GI，则由定理1知存在短正合列0→K→I→N→0，其中I∈I且K∈(X，I)-GI。考虑如下拉回图：

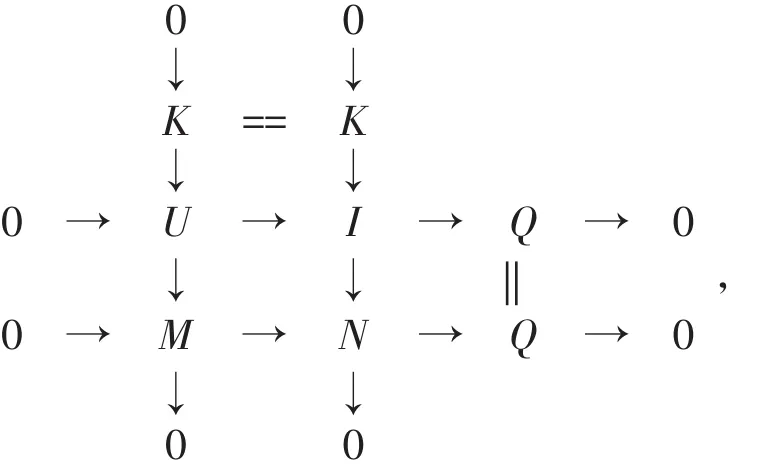
在短正合列0→K→U→M→0中K,M∈(X，I)-GI，从而U ∈(X，I)-GI。

考虑正合列0→U→I→Q→0，由定理1知Q ∈(X，I)-GI。

由定理2及文献[1]中命题1.4不难得到下面的推论。

推论1 模类(X，I)-GI关于直和因子封闭。

定理3 设N是左R-模，则以下条件等价：

(1)存在短正合列0→G1→G0→N→0，其中G0,G1∈(X，I)-GI；

(2)对任意正合列0→H1→H0→N→0，其中H0∈(X，I)-GI且Ext1R(I,H1)=0(任意I∈I)，都有H1∈(X，I)-GI。

证明 (2)⇒(1)显然成立，下面证明(1)⇒(2)。设存在短正合列0→G1→G0→N→0，其中G0,G1∈(X，I)-GI。由定理2知模类(X，I)-GI是内射可解的，所以N∈(X，I)-GI。由定理1知存在正合列0→K→I→N→0，其中I∈I且K∈(X，I)-GI。 对 任 意 正 合 列 0→H1→H0→ N → 0，其中H0∈(X，I)-GI且Ext1R(I,H1)=0(任意I∈I)，考虑如下拉回图：

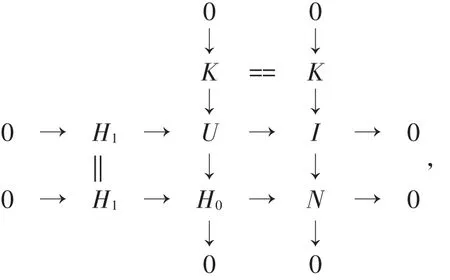
在正合列0→K→U→H0→0中K,H0∈(X，I)-GI，可见U ∈(X，I)-GI。用函子 HomR(I，-)作用于正合列0→H1→U→I→0可得长正合列

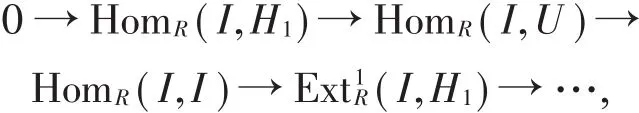
又因为I∈I ，Ext1R(I,H1)=0，所以0→H1→U→I→0可裂。H1是U的直和因子，由推论1可知H1∈(X，I)-GI。

[1]HOLM H.Gorenstein homological dimensions[J].J Pure Appl Algebra,2004,189(1-3):167-193.

[2]PAN Q X,CAI F Q.(X,Y)-Gorenstein projective and injective modules[J].Turkish J Math,2015,39:81-90.

[3]ENOCHS E E,JENDA O M G.Relative homological algebra[M].Berlin:Walter de Gruyter,2000:68-79.

[4]MENG F Y,PAN Q X.X-Gorenstein projective and Y-Gorenstein injective modules[J].Hacettepe Math,2011,40:537-554.

[5]ANDERSON F W,FULLER K R.Rings and categories of modules[M].New York:Spring Verlag,1992:177-241.

[6]佟文廷.同调代数引论[M].北京:高等教育出版社,1996:118-150.