关于卡诺图教学方法的探讨

王 辉 ，倪 春

(合肥师范学院安徽省微波与通信工程技术研究中心，安徽合肥230601)

“数字电子技术基础”课程是高等学校电子电气类专业必修的基础课，在教学计划中占有十分重要的地位。而卡诺图在该课程中应用广泛，是化简逻辑函数、分析和设计数字逻辑电路的重要工具，所以熟练掌握卡诺图及其应用方法对“数字电子技术基础”课程的学习大有裨益。1953年，美国Bell Laboratories工程师莫里斯·卡诺（Maurice Karnaugh）在维奇图的基础上提出了卡诺图[1-2]的概念。卡诺图作为一种描述逻辑函数的特殊方法，它将逻辑函数的逻辑变量分成两组，每一组变量取值组合按循环码的规则排列构成方格图，图中的每一个方格对应着逻辑变量的一个最小项。卡诺图作为真值表的一种变形画法，它具有以下特点[3]：(1)n变量逻辑函数对应的卡诺图具有2n个方格，与其全部最小项数相一致；(2)卡诺图中任意几何位置相邻的两个最小项（被称为几何相邻，又分为相接相邻、相对相邻、相重相邻3种情况），在逻辑上也是相邻的，反之亦然，即实现了几何相邻和逻辑相邻的一致性。卡诺图的这些特点，使得卡诺图广泛应用于逻辑函数化简、数字逻辑电路的分析和设计过程中[4-6]。

在“数字电子技术基础”课程的教学实践过程中发现，对于时序逻辑电路的状态分析，特别是异步时序逻辑电路的状态分析是很多学生的盲点，因为传统方法处理起来繁杂，特别是异步时序逻辑电路涉及时钟不同步问题，容易出错，很难掌握。针对该问题，文章基于卡诺图对该部分教学方法进行了一些改进，有效降低了时序逻辑电路分析问题的难度，特别是异步时序逻辑电路的分析难度。文章首先对卡诺图在同步时序逻辑电路中的应用[7-8]做一些总结和探讨，采用不同的分析思路，然后将其应用到异步时序逻辑电路的分析中，最后将卡诺图用到降维图法的教学中。

1 时序逻辑电路的状态分析

通过时序逻辑电路的状态分析[9-10]可以确定给定逻辑电路的逻辑功能，同时也为设计时序逻辑电路奠定了重要基础。尽管时序逻辑电路根据其时钟不同又有同步和异步之分，但是分析过程基本一致，按照图1所示过程进行。下面对由状态方程得出状态转移表这一难点过程进行分析。一般情况下，这一过程的计算是将现态逐个代入到状态方程中计算得到次态，如果状态方程比较复杂，计算量就较大，特别针对异步时序逻辑电路，时钟不同步，分析更困难。基于卡诺图的方法可有效降低计算复杂度，提升计算效率。

图1 时序逻辑电路分析步骤

1.1 同步时序逻辑电路的状态分析

例1假设某一同步时序逻辑电路具有状态方程如(1)式，求其对应的状态转移表。

解 画出3变量Q1Q2Q3现态卡诺图，如图2(a)所示，方格外的序列是现态，方格内对应的是次态。对于的计算，一般方法需要将8种现态组合带入状态方程计算，此处为提升计算效率对Q1状态方程分情况计算。观察方程形式，将分0和1两种情况：

（a）当=0时，对应次态卡诺图的左半边4个方格方程第2项为0，所以为与项等于1的概率是最小的，只有当取值为10的时候所以左半边4个方格只有当取值为010的时候，其余等于1，填入卡诺图相应位置如图2(b)所示；

（b）当=1时，对应次态卡诺图的右半边4当，所以右半边4个方格只有当取值为100的时候，，其余等于0，填入卡诺图相应位置如图2(c)所示；

对Q2状态方程进行化简变换得分以下两种情况：

（c）当时，对应次态卡诺图的上面一行4个方格，此时和项等于0的概率是最小的，只有当00的时候，所以上面一行4个方格只有当取值为000的时候

其余等于1，填入卡诺图相应位置如图2(d)所示；

（d）当时，对应下面一行4个方格，此时所以下面一行4个方格相应位置都填0，如图2(e)所示；

同样分析计算，最终得到状态转移卡诺图如图2(f)所示。

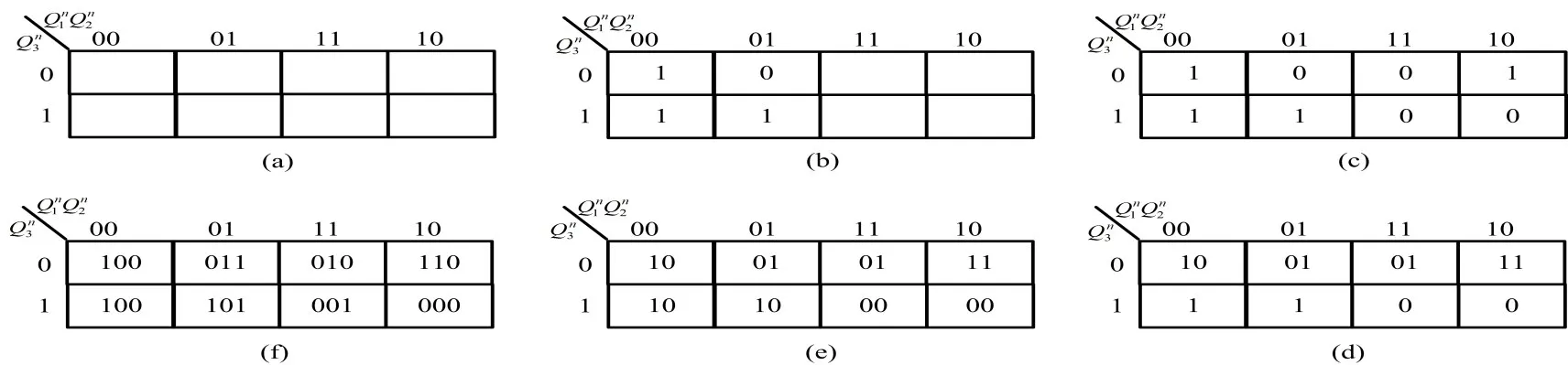
图2 同步时序逻辑电路状态转移分析

由上述分析发现，该分析方法思路清晰、简洁，只需要将一张卡诺图逐步按计算填充即可，而且一次可填充多个网格。若用一般方法计算(1)式的3变量次态需要计算24次，而现在只需要计算6次，有效提升了计算速度和计算效率。需要注意的是此处得到的计算次数仅针对(1)式，如果状态方程更复杂，计算次数会有不同，即使如此，该方法针对复杂的状态方程次态的计算，仍然可提升计算速度和计算效率。

1.2 异步时序逻辑电路的状态分析

例2假设某一异步时序逻辑电路具有状态方程如(2)式，求其对应的状态转移表。

解 对于异步时序逻辑电路，因为各状态方程时钟不同，特别是在时钟函数复杂的情况下，分析状态转移相当困难，是教学中的一个重难点。将上面同步时序逻辑电路的分析思路应用于分析异步时序逻辑电路，注意此处重点强调对时钟函数的分析。

（a）Q1触发沿为CP下降沿，当=0，只有取值为01的时候所以左半边4个方格只有当取值为001的时候，=0，其余等于1，填入卡诺图相应位置；当=1时，对应次态卡诺图的右半边4个方格，≡0，所以相应位置都填0，如图3(a)所示；

(b)Q2的触发沿为Q1的下降沿，从图3(a)中找出Q1现态为1次态为0对应的方格，如图3(a)箭头所示。在箭头所示方格，Q2被触发，满足方程=，其余方格保持不变即=，如图3(b)所示；

（c）Q3的触发沿为·CP+的下降沿，由(2)式可知，CP变化可能同时触发Q1、Q3，而Q2只有在Q1发生变化的情况下才有可能被触发，而Q2变化又有可能再次导致Q3被触发。根据以上分析，当取值为01时，Q3的触发沿为CP的下降沿，对应的方格标出箭头，如图3(b)所示；而在下一个CP脉冲到来之前，如果Q2出现了下降沿，那么Q3又被触发，对应方格标出箭头，如图3(c)所示。图3(b)，3(c)中箭头所在网格Q3被触发，即其余网格保持不变，最终结果如图3(d)所示。

由以上分析可知，该分析思路大大降低了异步时序逻辑电路的分析难度，即使对于时钟较复杂的情况，分析计算思路也较清晰，利用一张卡诺图逐步计算填充，避免了繁杂的分析计算，大大简化了分析计算过程。

图3 异步时序逻辑电路状态转移分析

2 降维图法

在利用数据选择器实现组合逻辑函数的过程中，如果组合逻辑函数的变量数大于数据选择器的地址端的个数，那么就需要利用降维图法。文献[3]中对降维过程的描述：设记图变量为x，对于原卡诺图中，当x=0时，原图单元值为F；当x=1时，原图单元值为G，则在新的降维图中对应的降维图单元中填入子函数xˉF+xG，其中F和G可以是0、1或某一变量，也可以是某一函数。这样的描述很拗口也不直观，对刚接触该方法的学生来说理解起来相当困难，计算起来也不方便。根据该知识点在实际教学过程的经验，处理如下：

新降维图中每个方格对应原卡诺图中的两个方格，如果这两方格中函数值都为F，那么新降维图中该方格里填F；如果这两方格函数值不同，那么变化顺序和记图变量变化一致的时候填记图变量的原变量，相反的时候填记图变量的反变量。

下面以4变量卡诺图降维成3变量降维图为例说明。如图4所示，以逻辑变量D为记图变量，则4变量卡诺图中的上面两行对应3变量降维图的上面一行，4变量卡诺图中的下面两行对应3变量降维图的下面一行。根据前面介绍的方法，可以方便地得到3变量降维图，其对应的各种不同情况，在图4中用①②③④标识出来。①、②为原图中值相同的情况，则降维图中对应的方格值也一样；③为变化顺序一致的结果，④为变化顺序相反的结果。

图4 降维过程

3 结束语

卡诺图贯穿整个“数字电子技术基础”课程，合理巧妙地利用卡诺图不仅可以快速降维，还能够简化对时序逻辑电路的分析，特别是大大降低了对异步时序逻辑电路的处理难度，只需要一张卡诺图，逐步分析计算填充，一次可填充多个网格，不仅思路清晰，而且降低了计算复杂度，有效提高了计算效率。卡诺图的应用广泛，文章仅通过举例详细阐述了卡诺图在降维图法以及时序逻辑电路分析中的应用，能够有效提升教学效果。

[1]KARNAUGH M.The map method for synthesis of combinational logic circuits[J].Transactions of American Institute of Electrical Engineers,1953,72(9):593–599.

[2]阎石.数字电子技术基础[M].北京:高等教育出版社,1998:28-31.

[3]王毓银.数字电路逻辑设计[M].北京:高等教育出版社,2005:31-34.

[4]薛俏.卡诺图在“数字逻辑电路”教学中的应用[J].辽宁科技大学学报,2012,35(6):618-622.

[5]钱萌.卡诺图的一图多用[J].安庆师范学院学报（自然科学版）,1999,5(3):53-55.

[6]何金保，骆再飞，诸葛霞.卡诺图在时序逻辑电路设计中的应用[J].宁波工程学院学报,2016,28(2):1-4.

[7]康华光.电子技术基础（数字部分）[M].北京:高等教育出版社，2014：282-286.

[8]胡长林.用卡诺图分析时序逻辑电路[J].电工教学，1992,15(2)：32-34.

[9]唐昌凡.时序逻辑电路分析方法剖析[J].四川师范学院学报（自然科学版）,1995,16(3):237-240.

[10]夏强胜，李娟.卡诺图在时序逻辑电路自启动教学中的应用[J].安庆师范学院学报（自然科学版）,2013,19(2):128-130.