一类分数阶时滞神经网络的Lyapunov稳定性判据①

蔡克珍，张海海

（安庆师范大学数学与计算科学学院，安徽安庆246133）

分数阶微积分即是关于任意阶微分和积分理论。近几十年来，它在工程、物理和经济等领域的建模中具有极为重要的应用价值[1-5]。由于分数阶导数是非局部的且具有非奇异核[6]，相比较于经典的整数阶模型，分数阶模型能够更好地描述系统的行为过程。

近年来，一些学者将分数阶算子引入到神经网络中，形成分数阶神经网络模型，从而更好地描述神经元的动力学行为。最近，文献[7-9]研究了不具有时滞的分数阶神经网络的稳定性。本文考虑如下Riemann-Liouville分数阶时滞神经网络的渐近稳定性

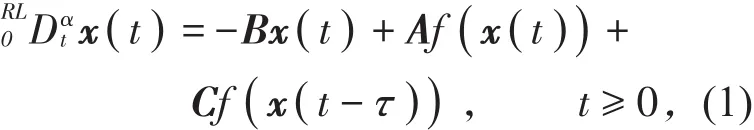
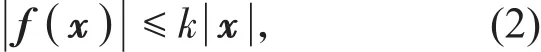
k是一个已知正常数。

在判定Riemann-Liouville分数阶时滞神经网络的渐近稳定性时，通过构造Lyapunov泛函的方法避免了计算其分数阶导数，所得结果描述为矩阵不等式，在计算上是方便可行的。

1 预备知识

本节给出分数阶微积分的相关定义和引理。

定义1[3]函数f的q＞0阶Riemann-Liouville分数阶积分的定义为

定义3 对任意的ε ＞0，存在δ=δ(ε ,t0)＞ 0，使得对任何初始条件，系统(1)的解x(t)满足不等式则称系统(1)的零解是稳定的。若系统(1)的零解是稳定的且则称它是渐近稳定的。

2 渐近稳定性判据

本节通过构造适当的函数来讨论系统(1)在Lyapunov意义下的渐近稳定性条件。

定理1若存在一个正定阵P和两个正常数β，γ使得

则系统(1)的零解是渐近稳定的，其中I是n维单位矩阵。

证明 构造如下的Lyapunov泛函

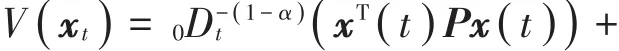
其中0＜α＜1，P，Q是正定阵。

因为P＞0，Q＞0，由定义1可知V( )xt是一个正定函数。由引理1可以得到V( )xt沿着系统

(1)轨迹的时间导数为

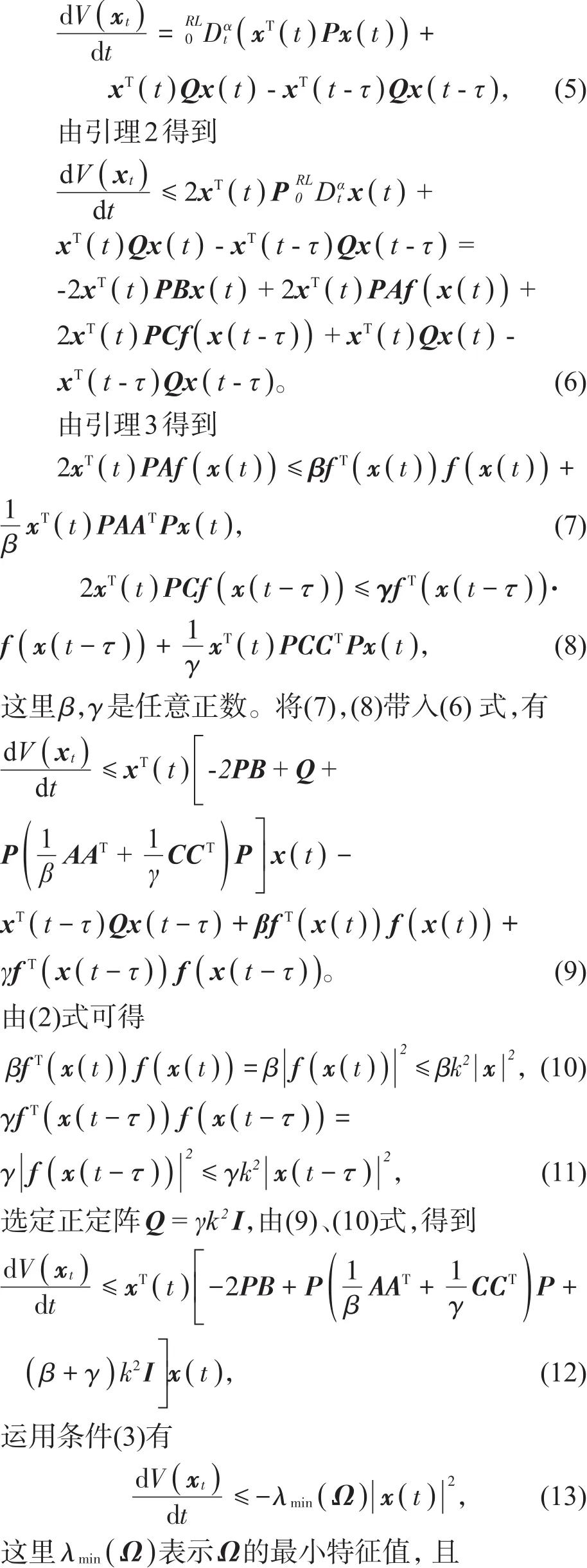
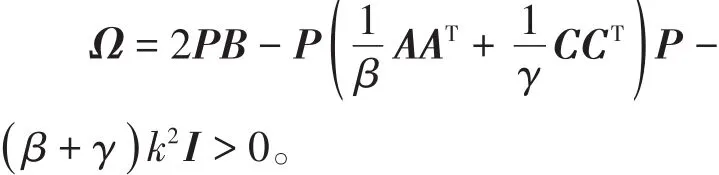
通过运用泛函微分方程的Lyapunov直接方法，得到系统(1)的零解是渐近稳定的。

在定理1中，令β=γ=1，可得到如下推论。

推论1 若存在正定阵P使得

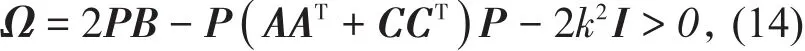
则系统(1)的零解是渐近稳定的。

3 数值例子

例1考虑一个二维的Riemann-Liouville分数阶时滞神经网络：

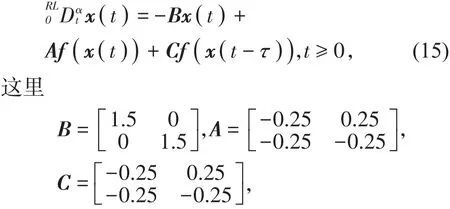
因此满足定理1的条件，所以系统(15)的零解是渐近稳定的。

对于数值模拟，分别考虑如下5种不同的初始状态：

图1和图2分别描述了对应于这些初始值的状态轨迹，证实了定理1是有效的和可行的。

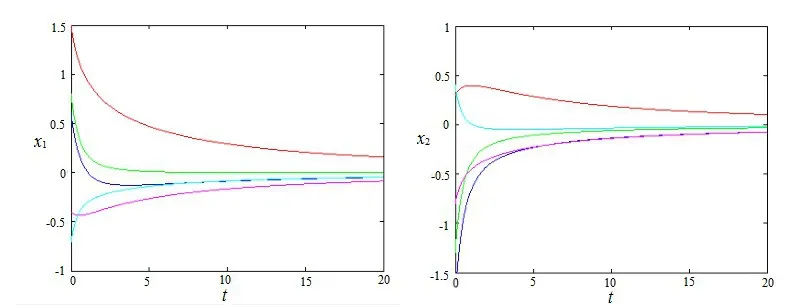
图1 α=0.8，τ=0.4的神经网络在不同初始值下的轨迹

图2 α=0.4，β=0.2的神经网络在不同初始值下的轨迹

4 结 论

本文构造了一个适当的泛函来讨论Riemann-Liouville分数阶时滞神经网络的渐近稳定性，该方法避免了计算Lyapunov泛函的分数阶导数，直接计算Lyapunov泛函的一阶导数来检验稳定性，利用矩阵不等式描述所得结果，在计算上也是方便可行的。

[1]MILLER K S,ROSS B.An introduction to the fractional calculus and fractional differential equations[M].New York:John Wiley&Sons,1993:44-229.

[2]PODLUBNY I.Fractional differential equations[M].Kosice:Academic Press,1999:1-220.

[3]KILBAS A A.SRIVASTAVA H M.TRUJILLO J J.Theory and applications of fractional differential equations[M].Amsterdam:Elsevier Science BV,2006:1-205.

[4]LI C P,DENG W H.Remarks on fractional derivatives[J].Appl Math Comput,2007,187(2):777-784.

[5]LIU Y.On piecewise continuous solutions of higher order impulsive fractional differential equations and applications[J].Appl Math Comput,2016,s287-288(C):38-49.

[6]WANG J R,LV L L,ZHOU Y.New concepts and results in stability of fractional differential equations[J].Commun Nonlinear Sci Numer Simul,2012,17(6):2530-2538.

[7]CHEN J J,ZENG Z G,JIANG P.Global mittag-leffler stability and synchronization of memristor-based fractional-order neural networks[J].Neural Networks,2014,51(3):1.

[8]LI H L,JIANG Y L,WANG Z,ZHANG L,et al.Global Mittag-Leffler stability of coupled system of fractional-order differential equations on network[J].Appl Math Comput,2015,270:269-277.

[9]REN F L,CAO F,CAO J.Mittag-Leffler stability and generalized Mittag-Leffler stability of fractional-order gene regulatory networks[J].Neurocomputing,2015,160:185-190.

[10]LIU S,JIANG W,LI X,et al.Lyapunov stability analysis of fractional nonlinear systems[J].Appl Math Lett,2016,51:13-19.