三次函数考什么?
■福建省龙岩市永定区城关中学 童其林(特级教师)
三次函数是一类重要函数,三次函数的导数为二次函数,而二次函数是高中数学中的重要内容,并且三次函数可交汇函数、不等式、方程等众多知识点,所以三次函数已经成为高考命题一个新的热点和亮点。下面归纳整理三次函数的主要考点,并剖析三次函数有关问题的基本思路,以飨读者。
一、考查三次函数的单调性
如何定义三次函数?形如y=a x3+b x2+c x+d(a≠0)的函数,称为三次函数(从函数解析式的结构上命名)。三次函数的导数y'=3a x2+2b x+c(a≠0),把Δ=4b2-1 2a c叫作三次函数的导函数的判别式。
一般地,当b2-3a c≤0时,三次函数y=数;当时,三次函数y=a x3+在R上有三个单调区间,根据a>0,a<0两种情况进行分类讨论。
例1内单调递减,则a的取值范围是 。
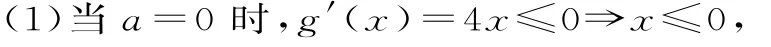
解析:问题转化为上恒成立,求a的取值范围。即g'(x)<0在(-∞,0)上恒成立,所以a=0适合题意。
(2)当a>0时,二次函数g'(x)开口向上,不可能有上恒成立,所以a>0不合题意。
(3)当a<0时,二次函数g'(x)开口向下,其对称轴x=2(a-1)>0,画出草图知,3a只需满足


点评:题目没有说是三次函数,所以要讨论a=0的情形。
二、考查三次函数的极值
当Δ>0时,三次函数y=f(x)在(-∞,+∞)上的极值点有两个。
当Δ≤0时,三次函数y=f(x)在(-∞,+∞)上不存在极值点。
可以用表1说明三次函数单调性与极值点的关系。在R上是单调函

表1
其中是方程f'(x)=0的根,且。
例2 已知函数既有极大值又有极小值,则实数a的取值范围是 。

又因为f(x)既有极大值又有极小值,所以f'(x)=0必有两个不等的解,Δ=4a2-4a-8>0。
解得a<-1或a>2,所以a的取值范围是(-∞,-1)∪(2,+∞)。
点评:通过求函数的导数,将函数问题转化为一元二次方程来探究,充分体现了函数与方程相互转化的解题思想与解题策略。
三、考查三次函数的最值问题

例3 函数f(x)=x3-3x+1在闭区间[-3,0]上的最大值、最小值分别是( )
A.1、-1 B.1、-1 7
C.3、-1 7 D.9、-1 9
解析:令f'(x)=0,则3x2-3=0,两根为1和-1,但1∉[-3,0],不计算。
计算端点和极大、极小点的值,得f(-3)

四、考查三次函数恒成立问题
例4 (2 0 0 8年江苏高考数学试卷第1 4题)设函数若对于任意x∈[-1,1]都有f(x)≥0成立,则实数a的值为 。
分析:将f(x)≥0中的a,x分离,然后求函数的最值。
解:若函数f(x)=a x3-3x+1(x∈R)对于任意x∈[-1,1]都有f(x)≥0成立,则函数f(x)=a x3-3x+1对于任意x∈[-1,t≤2)单调递增ymax=h(2)=4;当t单调递减,ymax=h(2)=4。由题意知①②③应同时成立,故a=4。

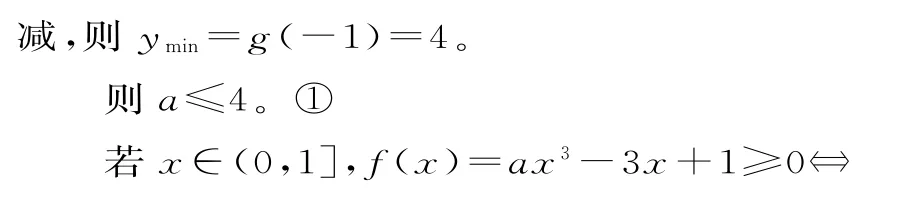



五、考查三次方程根的问题


时,不等式恒成立,故函数是单调递增的,方程f(x)=0仅有一个实根。f(x)极大值点和极小值点在x轴同侧,图像均与x轴只有一个交点,所以方程f(x)=0有且只有一个实根。②若,即函数y=f(x)极大值点与极小值点在x轴异侧,图像与x轴必有三个交点,所以方程f(x)=0有三个不等实根。

③若f(x1)·f(x2)=0,即f(x1)与f(x2)中有且只有一个值为0,所以方程f(x)=0有三个实根,其中两个相等。
同理,也可讨论三次函数当a<0时的情形。
例5(2 0 1 2年全国大纲卷理科第1 0题)已知函数y=x3-3x+c的图像与x轴恰有两个公共点,则c=( )。
A.-2或2 B.-9或3
C.-1或1 D.-3或1
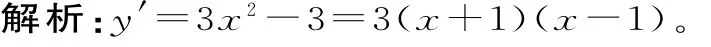
当y'>0时,x<-1或x>1;
当y'<0时,-1<x<1。
所以函数的递增区间为(-∞,-1)和(1,+∞),递减区间为(-1,1)。
因此,x=-1时,取得极大值;x=1时,取得极小值。
要使函数图像与x轴恰有两个公共点,只需:f(-1)=0或f(1)=0,即(-1)+c=0或1-3+c=0,所以c=-2或c=2。
故答案为A。-3×
(责任编辑 徐利杰)
(上接第3 2页)

表2
(2)将上述调查所得到的频率视为概率。现在从该地区电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X。若每次抽取的结果是相互独立的,求X的分布列,期望和方差。附:

解析:(1)由频率分布直方图可知,在抽取的1 0 0人中,“体育迷”有2 5人,从而2×2列联表如下(表3):由2×2列联表中数据代入公式计算,得:

表3

因为3.0 3 0<3.8 4 1,所以没有理由认为“体育迷”与性别有关。
(2)由频率分布直方图知抽到“体育迷”的频率为0.2 5,将频率视为概率1,即从观众4
中抽取一名“体育迷”的概率为,由题意,x~,从而X的分布列为:
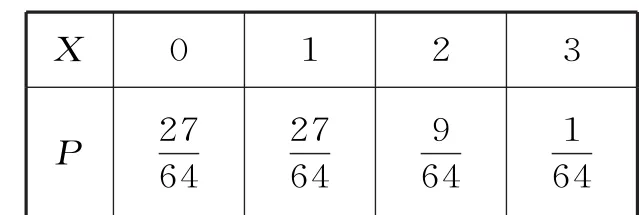
X 0 1 2 3 P 2 7 6 4 2 7 6 4 91 6 46 4
点评:二项分布是一种常见的离散型随机变量的概率分布,利用二项分布可以快速地写出随机变量的分布列,从而简化了求随机变量某一个具体概率值的过程。利用二项分布来解决实际问题的关键在于在实际问题中建立二项分布的模型,也就是看它是否是n次独立重复试验,随机变量是不这n次独立重复试验中某事件发生的次数,满足这两点的随机变量才服从二项分布,否则就不服从二项分布。
——基于Web of Science核心数据库(1975-2019)的知识图谱分析

