用数学建模法搞定随机变量的分布列

■陕西省洋县中学 李 勇

数学建模法是一种极其重要的思想方法,它是把实际问题抽象成数学语言符号,构建数学模型,从而解决实际问题。其一般步骤是:分析实际问题→构建数学模型→建立数学关系式→解数学关系式→回归实际问题。

建模法在随机变量的分布列考点的应用中,主要体现在古典概型、超几何分布概型、二项分布概型(特殊的二项分布(两点分布)和普通的二项分布)的解题中。下面结合近几年的高考动态,进行探究。

模型1：运用古典概型求解分布列

离散型随机变量的分布列不仅能清楚地反映其所取的一切可能的值,而且也能清楚地看到取每一个值的概率大小。概率的求解离不开古典概型,因此古典概型是完善分布列求解的有力工具。

例1 (2 0 1 5年福建省理科卷)某银行规定:一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定。小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试。若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定。

(1)求当天小王的该银行卡被锁定的概率;

(2)设当天小王用该银行卡尝试密码次数为X,求X的分布列。

解析：(1)设“当天小王的该银行卡被锁定”的事件为A,则P(A)==

(2)依题意得,X所有可能的取值是1,2,3。

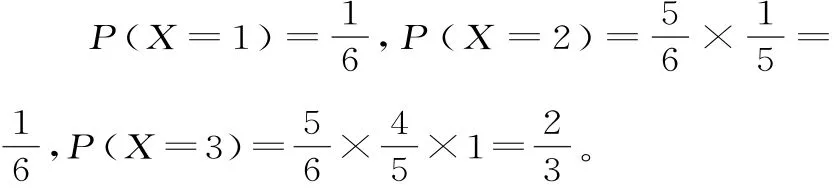
所以X的分布列为:

X 1 2 3 P 112 663

点评:求离散型随机变量的概率分布首先要清楚离散型随机变量的可能取值,以及当随机变量取这些值时所对应的事件的概率是多少,通常化归到古典概型的概率模型上计算出概率值后,再列出离散型随机变量概率分布列即可。

模型2：运用超几何分布模型求解分布列

分布列的求解在形式上常由较明显的两部分组成,如“男生、女生”,“正品、次品”,“优、劣”等字眼构成,符合这几种形式就是超几何分布模型。

例2 (2 0 1 7年山东省理科第1 8题)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用。现有6名男志愿者和4名女志愿者,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示。

(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的频率;

(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望E(X)。

解析：(1)记接受甲种心理暗示的志愿者包含A1但不包含B1的事件为M,则P(M)=

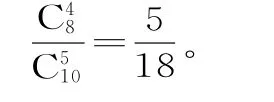
(2)由题意可知X可取的值为:0,1,2,3,4。因此,X的分布列为:

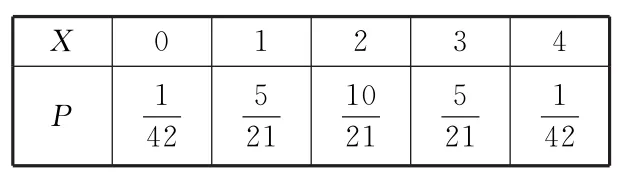
X 0 1 2 3 4 P 151 051 4 22 12 12 14 2

X的数学期望是:1=2。4 2

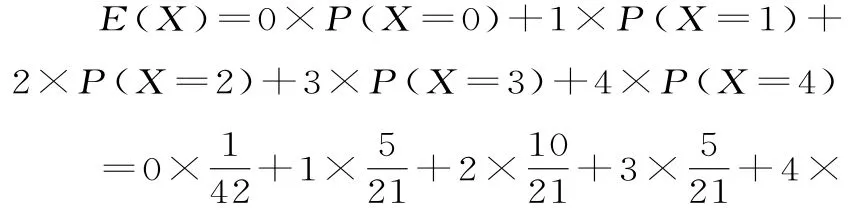
点评:解答此类题目的关键在于先分析随机变量是否满足超几何分布,如果满足超几何分布的条件,则直接利用超几何分布的概率公式求解。当然,本题也可通过古典概型解决,但利用超几何分布概率公式简化了对每一种情况的分析,因此要简单一些。

模型3：运用二项分布模型求分布列

1.特殊的二项分布(两点分布)模型

两点分布是一次试验中只会出现两种结果,在二项分布中,当n=1时即为两点分布,故两点分布是特殊的二项分布。

例3 某商店试销某种商品2 0天,获得如下数据:

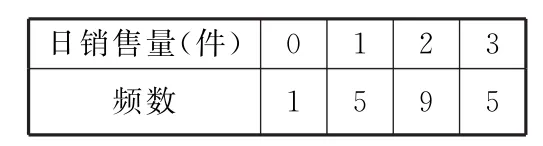
表1

试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货。将频率视为概率。

(1)求当天商店不进货的概率;

(2)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。

解析：(1)P(“当天商店不进货”)=P(“当天商品销售量为0件”)+P(“当天商品销售量为1件”)=1+5=3。2 02 01 0

(2)由题意知,X的可能取值为2,3。

P(X=2)=P(“当天商品销售量为1件”)=;

P(X=3)=P(“当天商品销售量为0件”)+P(“当天商品销售量为2件”)+P(“当天商品销售量为3件”)=故X的分布列为:

?

点评:两点分布的题型特征是随机变量的可能取值只有2个,计算其中一个随机变量取值相应的概率后,另一个随机变量相应的概率就可以直接计算,也可以利用对立事件的概率之和为1计算,它属于特殊的二项分布问题。

2.普通的二项分布模型

二项分布是有放回地抽样检验问题,在实际操作中,从大批产品中抽取少量样品的不放回检验,可以近似看作此类模型。它在一次试验中,事件发生与否二者必居其一;试验是独立重复进行的。传解众目随名查媒某对 。机的 观例下公地某抽收众面司区类4取视 进是 为电体了情行根电了视育1况0视了观节 调据 0,

图1

调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,如图1所示。

将日均收看该体育节目时间不低于4 0分钟的观众称为“体育迷”。

(1)根据已知条件完成下面的列联表(表2),并据此资料说说你是否认为“体育迷”与性别有关。

(下转第3 9页)