Karabut系统的亚纯首次积分

曲婧佳, 杨双羚, 冯 雪

(1.空军航空大学 基础部， 吉林 长春 130022;2.吉林建筑大学城建学院, 吉林 长春 130114)

0 引 言

为了研究理想不可压缩的重质流体在平底上的无涡旋平稳运动,Karabut考虑了如下边值问题的解[1-3]:

(1)

设式(1)具有如下形式的解：

W=θ2W1(χ)+θ4W2(χ)+θ6W3(χ)+…

这种形式的解对应了浅水扩张现象。进一步假设Wj(χ)是关于cosh-2(χ/2)的多项式函数,并记ζ=eχ。那么,上式可改写为：

W=E1(θ)ζ+E2(θ)ζ2+E3(θ)ζ3+…

这种序列由Witting在文献[4]中提出,同时,他也给出了系数Ej的递推公式。Karabut证明：对于θ=mπ/n(m,n∈Ζ)，Witting序列的精确求解等价于求解一组n元一阶微分方程组。具体引入函数

Pj(χ)=W(ζω2j-2)

ω=eiθ,j=1,2,…，n

满足方程组:

(2)

因此,为了求解边值问题(1)具有Witting序列形式的解,我们只需要解积分方程组(2)，并取W=P1。

Karabut在文献[1，3]分别证明了系统(2)在θ=π/3,θ=π/4是可积的, 并给出了Witting序列的精确表达式。文献[5]研究了该系统的非哈密顿意义下的可积性。这里用不同的方法研究该系统亚纯首次积分的最大个数问题。文中主要考虑θ=π/5的情形。记

则系统(2)可以改写成关于变量fj的标准形式的常微分方程组:

做时间尺度变换

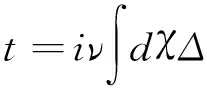
并记yi:=fi,则Karabut等价于如下系统:

(3)

式中,“·”表示对时间t的求导。

数值模拟显示,Karabut系统(3)具有复杂的动力学行为。文中将从不可积性的角度去认识该系统的拓扑结构。如果该系统有(n-1)个函数独立的首次积分,一般我们称一个微分动力系统是完全可积的。

1 主要结果及证明

定理1Karabut系统(3)至多有三个函数独立的亚纯首次积分。

定理2Karabut 系统(3)不是亚纯完全可积的。

通过分析系统(3)沿某个非平衡特解的变分方程的Galois群的性质,去证明该系统至多只有三个函数独立的首次积分。因为系统(3)是相对于权(1,1,1,1,1)的拟齐次系统,所以它存在自相似解:

其中,非零向量c=(c1,c2,c3,c4,c5)满足代数方程组:

c1+c3c5-c2c4=0

c2+c4c1-c3c5=0

c3+c2c5-c1c4=0

c4+c1c3-c2c5=0

c5+c2c4-c1c3=0

(4)

经计算,得到一组解

c=(-i,-1,1,i,0)

系统(3)沿着该自相似解的变分方程是

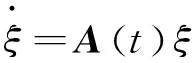
(5)

其中,A(t)是系统(4)沿着该自相似解的Jacobi矩阵,即

做变换ξ=t-1χ,方程(5)变为

(6)

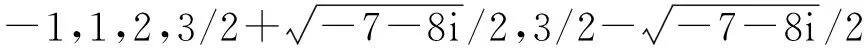
进一步得到系统(6)的一个子系统,法向变分方程

(7)

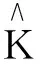
参考文献：

[1] Karabut E A. Summation of the witting series in the solitary wave problem[J]. Siberian Mathematical Journal,1995,36(2):287-304.

[2] Karabut E A. Asymptotic expansions in the problem of a solitary wave[J]. Journal of Fluid Mechanics,1996,319:109-123.

[3] Karabut E A. Summation of the witting series in the solitary-wave problem[J]. Appl. Mech. Tech. Phys.,1999,40:36-45.

[4] Witting J. On the highest and other solitary waves[J]. SIAM Journal on Applied Mathematics,1975,28(3):700-719.

[5] Christov O. Non-integrability of the karabut system[J]. Nonlinear Analysis: Real World Applications,2016,32:91-97.

[6] Ziglin S L. Branching of solutions and nonexistence of first integrals in Hamiltonian mechanics[J]. Functional Analysis and its Applications,1982,16(3):181-189.

[7] Morales-Ruiz J J, Ramis J P. Galoisian obstructions to integrability of Hamiltonian systems[J]. Methods Appl. Anal.,2001,8(1):33-96,97-112.