不定积分的8种计算方法

丁伯伦， 凌婷婷， 荣婉君， 朱晓明

(安徽信息工程学院 基础教学部， 安徽 芜湖 241000)

0 引 言

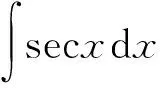
1 形式变换法

方法1首先可以巧妙地借助余割函数的不定积分结果[1]，计算出正割函数的不定积分。

由于

基于正割函数与余割函数的关系，可得：

ln|secx+tanx|+C

这里采用恒等变换的方法，由于正割函数与余割函数有这样的一个转换关系，可以借助于余割函数的积分结果，这样的方法是借用巧力，计算起来也更简便，但前提条件是必须要熟悉余割函数积分的计算结果。

方法2由于正割函数等于余弦函数的倒数，因此可以从余弦函数入手。对于余弦函数而言,最直观的恒等变换是利用二倍角公式

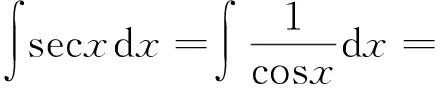
方法2与方法3本质上是相同的，均采用恒等变换的方法。先是对余弦函数进行变型，利用二倍角公式展开将被积函数转化为较易的形式，然后采用凑微分的方法给予解决，这种方法大大优化了积分的计算过程，提高了解题效率。

2 凑微分法

方法4先将正割函数进行巧妙的变形，变为较易积分的形式，可采用第一类换元积分法(凑微分)进行积分，计算过程将变得简单明了[2]。

方法5基于方法4的思想，可以做下面变型，然后仍然依靠凑微分的方法进行积分。

ln|secx+tanx|+C

对于正割函数的不定积分，方法4与方法5是比较常见的,也是最常用的计算方法，在大多数教材[2-4]中都给予指出。它们在解题思路上是一致的，只是在结果上呈现出不同的表现形式。在求积问题上，凑微分的这两种方法对解题思路要求极高，需要大量的熟悉与练习，也可当做一种固定的解题模式进行记忆。

3 万能公式法

方法6可以采用高中所学的三角函数的万能公式来解题。

由于

令

而

因此可得：

利用万能公式来计算也是一种不错的选择，将关于三角函数的不定积分问题转化为有理函数的不定积分问题。因此，只需计算有理函数的积分即可，这里选择的是有理函数积分问题中的积化和差的积分方法[5]。

4 分布积分法

方法7对于正割函数的不定积分问题，可利用分部积分法给予解决[6]。

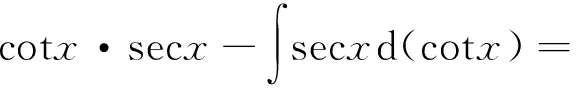
方法7在方法选择上比较创新，利用分部积分法解题，巧妙利用cotx·tanx=1，可构造出分部积分法的一般式，最后通过凑微分法得出结果。这里将不定积分计算的两大积分法紧密地联系在一起，构思较新颖，开阔了这类积分问题的新解法。

5 方程组求解法

方法8计算有些函数的不定积分问题可以将其转化为求解方程组的问题[7-8]，在有些情况下可以降低解题难度，提高计算效率。而对于正割函数的不定积分计算显然是可以的。

设

则

令

则

化简上式可得：

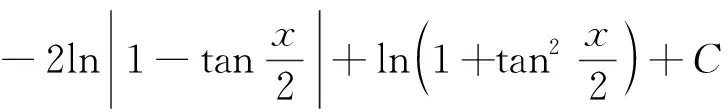
(1)

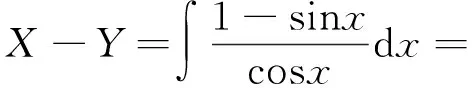
同理，令

化简可得：

(2)

结合方程(1)与方程(2)，可得到一个二元线性方程组，则有

参考文献：

[1] 同济大学数学系.高等数学(上)[M].北京:高等教育出版社,2003:199.

[2] 华东师范大学数学系.数学分析(上)[M].北京:高等教育出版社,2002:184-185.

[3] 费为银,王传玉,项立群.高等数学(上)[M].合肥：中国科学技术大学出版社,2009:143.

[4] 高汝熹.高等数学:微积分[M].武汉：武汉大学出版社,1998:234-235.

[5] 胡静波.高等数学的发散思维培养研究[J].湖北科技学院学报,2013,33(12):29-30.

[7] 毛北行,李新芳.方程组在求解不定积分中的应用[J].河南工学院学报，2013,21(6):99-100.

[8] 吴维峰.对不定积分一题多解的分析[J].高等数学研究,2010,13(6):11-13.