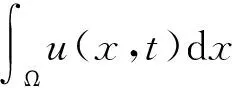Neumann边界条件下非局部扩散方程解的爆破
张敏华
(阳光学院 基础教研部, 福建 福州 350015)
0 引 言
文中主要工作是考虑下列Neumann边界条件下非局部扩散方程:
(1)
其中,Ω是一个光滑有界的区域,J:RN→RN,G:RN→RN是连续非负并且径向对称的函数,在单位球内是紧支集的,使得

式(1)右边第一个积分项考虑的是个体从其他方向到达或者离开点x;式(1)右端的第二个积分项描述的是个体进入或者离开区域的流量,根据函数g的符号。这就是所说的Neumann边界条件[1]。而且,文中在方程中增加了一个反应项up(x,t),探求问题的爆破解的情况。
在先前的文献中关于非局部扩散过程已经得到了相关的关注。与文献[2]提及的一样,u(x,t)可以表示为单个群种在(x,t)点的密度,J(x-y)表示为从点y到x的概率分布;那么

从别的方向到达点x的到达率。
对于Neumann边界条件下的非局部扩散,Cortazar等[3-4]研究了相类似的问题,形式如下:

1 局部存在唯一性
其中,t0是一个固定的点。
式(1)中的u,t分别用w,s来代替,可得:
因此考虑相关的积分系统:
根据此方程,建立下列算子。
定义1令Φ:Bt0→Bt0定义如下:

(2)

证明 考虑0 |Φw0,g[w(x,t1)]-Φw0,g[w(x,t2)]|= 其中,|Ω|代表区域Ω的测度。因此,当t∈(0,t0],算子Φw0,g是连续的。 当t=0时: |Φw0,g[w(x,t)]-w0(x)|= 由上述两个估计可得,对于每一个t∈[0,t0],算子Φw0,g是连续的。 证毕。 C=C(Ω,J,G,p,‖w‖Bt0,‖z‖Bt0) 使得: |‖Φw0,g[w(x,t)]-Φz0,h[z(x,t)]‖|≤‖w0-z0‖L (3) 证明 |Φw0,g[w(x,t)]-Φz0,h[z(x,t)]|≤ ‖w0-z0‖L C=max{2K1|Ω|+pηp-1,K2} 证毕。 作为上面两个引理的结果,有下面的解的存在性和唯一性定理。 |‖Φw0,g[w(x,t)]-Φz0,h[z(x,t)]‖|≤Ct0‖w-z‖Bt0 最后,式(1)两边关于时间t积分可得: 再关于x积分 考虑到J的对称性和Fubini定理有: 推论1假设u,v是式(1)的解,其中初始值和边界值分别为u0,v0,g,h。那么对于每一个t0>0,存在一个只依赖于t0的常数C1满足: 证明 由u,v的定义可知 根据引理2可知: 如果Ct0<1可得: 推论2令u∈Bt0,那么u是式(1)的解,当且仅当: 证明 式(1)可以表示为: 两边分别乘上eA(x)s,有: 两边从0到t积分得: 证毕。 给出式(1)的比较原理。下面首先给出上下解的定义。 改变不等号的方向可以定义下解。 x∈Ω,t>0 证明 假设在某些点w(x,t)是负的。令 θt(x,t)=e-λtw(x,t)(λ>0,λ≥2sup|c|) 如果假设在(x0,t0)处θ达到负的最小值,其中t0>0,那么 θt(x0,t0) =-λe-λt0w(x0,t0)+e-λt0wt(x0,t0)≥ (c-λ)θ(x0,t0)>0 这个与θ(x,t)在(x0,t0)处θ达到负的最小值矛盾。证毕。 证明 假设p>1。在式(1)的第一个方程两边关于x∈Ω积分,再应用Fubini定理有: 因为g≥0,G是非负函数,那么有: 反之,假设p≥1。考虑下列的ODE问题: 因为对于t>0,p≤1,z(t)>1,那么z(t)>zp(t)。因此z(t)是式(1)的全局上解。因此根据比较原理可知u是全局的。 参考文献: [1] C Cortazar, M Elgueta, J D Rossi, et al. Boundary fluxes for nonlocal diffusion[J]. Differential Equations,2007,234:360-390. [2] P Fife. Some nonclassical trends in parabolic and parabolic-like evolutions[J]. Trends in Nonlinear Analysis,2003,136:153-191. [3] C Cortazar, M Elgueta, J D Rossi, et al. How to approximate the heat equation with Neumann boundary conditions by nonlocal diffusion problems[J]. Arch. Ration. Mech. Anal.,2008,187(1):137-156. [4] F Andreu-Vaillo, J M Mazon, J D Rossi, et al. Nonlocal diffusion problem[J]. Mathmatical Surveys and Monographs, Ameritican Mathematical Society,2010,96:165. [5] Wang YuLan, Chen Qiong. Blowup analysis for a nonlocal diffusion equation with reaction[J]. Journal of Sichuan University,2012,49:299-303. [6] Liviu I Ignat, Julio D Rossi. A nonlocal convection-diffusion equation[J]. Journal of Functional Analysis,2007,251:399-437. [7] 李中平,徐思.杜宛娟.快速扩散方程的第二临界指标及解的生命跨度[J].数学物理学报,2012,32A(5):904-913. [8] 张敏华.一类非局部渗流扩散方程的爆破分析[J].福建教育学院学报,2016,17:118-121.









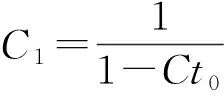

2 比较原理







3 全局存在和爆破