电动汽车机电复合制动力矩分配

崔高健， 吴晓东， 李绍松， 刘小勇

(1.长春工业大学 机电工程学院， 吉林 长春 130012；2.长春工业大学 汽车工程研究院， 吉林 长春 130012)

0 引 言

电动汽车的机电复合制动系统由再生制动系统和液压制动系统复合而成[1]。再生制动既能提供制动力矩，还能回收部分制动能量，做到快速响应。液压制动可提供较大的制动力矩，是高强度制动时制动力矩的主要来源。如何合理地分配机电复合制动力矩成为当前的关键问题之一[2]。

目前来说，普遍研究的方法是根据理想分配曲线(I曲线)和ECE法规约束结合诸如滑膜控制、模糊控制、分层控制等各种控制方法来实现制动力矩的分配[3-5]。但此类方法多以回收更多的制动能量为主要目的，没有考虑到制动力矩能否得到最大利用的问题。因此,文中以后轮驱动纯电动汽车为研究对象，在紧急制动情况下，提出了一种基于模型预测控制的电动汽车机电复合制动力矩分配策略：首先根据汽车测量值估算出当前路面的附着系数及其对应的最佳滑移率；然后利用模型预测控制，以前后轴的制动力矩为输入，车轮滑移率为输出，对滑移率进行跟踪控制，完成前后轴的制动力矩分配；最后为保证良好的制动踏板感觉，在对后轮上的制动力矩进行分配时，给液压制动力矩一个稳定值，其余所需制动力矩由再生制动系统提供。

该方法利用模型预测控制善于处理约束及滚动时域优化的特点，以最佳滑移率为跟踪目标，既能做到制动力矩最佳利用，又能做到防抱死效果。

1 系统模型

1.1 汽车动力学模型

文中以后轮驱动纯电动汽车为研究对象，假设汽车始终在平直路面上行驶，忽略转向、空气阻力和滚动阻力，只考虑汽车纵向运动。

后轮驱动纯电动汽车动力学图如图1所示。

图1 后轮驱动纯电动汽车动力学图

汽车运动方程以及前、后轮运动公式分别为：

(1)

(2)

(3)

式中:m----汽车中心质量；

v----车速；

J----车轮转动惯量；

Jpt----驱动产生的转动惯量；

R----车轮半径；

Fxf,Fxr----分别为前、后轮纵向力；

Tbf,Tbr----分别为前、后轮制动力矩；

Td----驱动力矩；

ωf,ωr----分别为前、后轮的车轮转速。

车轮滑移率模型为：

(4)

对式(4)求导：

(5)

式中:λf,λr----分别为前、后车轮的滑移率。

1.2 轮胎模型

滑移率与轮胎/路面摩擦系数的关系可用Burckhardt模型表示[6]：

μ(λ)=c1(1-e-c2λ)-c3λ

(6)

式中：c1,c2,c3----路面因子。

五种路面的路面因子见表1。

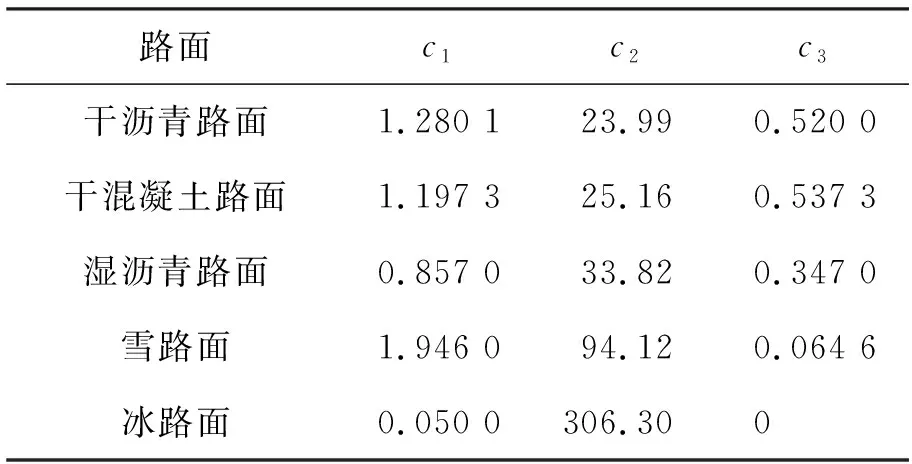
表1 五种路面的路面因子取值

车轮纵向力及垂直载荷为：

Fxi=μi(λi)Fzi,i=f,r

(7)

(8)

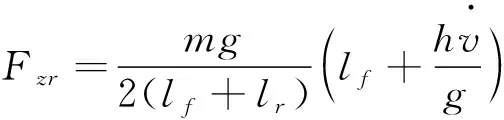
(9)

式中:μf,μr----分别为前、后轮与路面的摩擦系数；

Fzf,Fzr----分别为前、后轮的垂直载荷；

g----重力加速度；

h----汽车质心到路面距离；

lf,lr----分别为汽车质心到前后轴距离。

1.3 电池模型

电池的SOC及充电电流为[7]：

(10)

(11)

式中:SOCact----电池SOC实际值；

SOCini----电池SOC初始值；

Qc----电池总的能量容积；

U0----电池开路电压；

Pr----电机再生制动所产生的功率；

Rb----等效电池内阻；

Ib----电流。

2 路面附着系数估计/最佳滑移率的确定

汽车在紧急制动时，如果路面附着系数发生变化，那么汽车的制动效果也将发生巨大变化。尤其路面附着系数的变化将影响最佳滑移率，所以，文中对Burckhardt模型做了修改，使其可以应用于所有路面。

将式(6)及表1对应的五条曲线用插值的方法表示成适用于所有路面的形式，其模型如图2所示。

图2 滑移率-摩擦系数-路面附着系数三维模型

当确定了路面附着系数之后,同时也确定了其对应的滑移率与摩擦系数的曲线，如图3所示。

图3 最佳滑移率示意图

当曲线达到最大值点(λd,μmax)，此时的附着系数为最大值，汽车制动力矩的利用率达到了最大，且此时的滑移率较小，因此点λd即为当前路面的最佳滑移率。只需根据三维模型选出其对应的最大值点即可获得最佳滑移率。

3 制动力矩分配策略

机电复合制动力矩分配的控制结构如图4所示。

图4 制动力矩分配控制框图

首先以上一环节计算出的最佳滑移率为理想值，利用MPC方法对滑移率进行跟踪控制，实现前后轴的制动力矩分配；然后对驱动后轮的制动力矩采用良好踏板感觉(GDF)分配策略，完成再生制动力矩与液压制动力矩的分配。

3.1 基于MPC的前后轴制动力矩分配

联立式(1)～式(4)，将其代入式(5)，并表示成如下形式[8]：

x(k+1)=Ax(k)+Bu(k)

y(k)=C·x(k)

(12)

式中:u----控制输入,u=[Tbf,Tbr]T；

x----状态变量,x=[λf,λr]T；

y----控制输入,y=[λf,λr]T。

定义P为预测时域，M为控制时域，且P≥M≥1。定义滑移率的理想值r(k)=λd。

控制问题的优化目标函数为[9]：

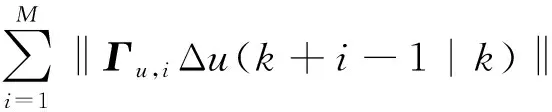
(13)

式中:k+i|k----k时刻对第k+i的估计；

Γyi、Γui----权重矩阵；

Δu(k)----控制输入在k时刻的增量,Δu(k)=u(k)-u(k-1)。

考虑到紧急制动时输入、输出等存在的一些约束问题，需要列举可能存在的一些约束：

|ΔTi(k+j|k)|≤ΔTmax,

|Ti(k+j|k)|≤Tmax,j=0,1,…,M-1

0≤λi(k+j|k)≤1,j=0,1,…,P

(14)

式(13)和式(14)即为所要求解的问题。利用二次规划算法(QP)求解优化目标函数，得到控制输入增量的序列，将此序列的第一个元素与上一时刻控制输入相加，即为当前所需的控制输入，即汽车前后轴的制动力矩。在以后的每个采样时刻重复以上操作，刷新优化目标函数求解[10]。

3.2 后轴制动力矩分配

对于后轮驱动纯电动汽车，其前轴制动力矩完全由液压系统提供，而后轴制动力矩则由液压制动力矩和再生制动力矩共同提供，考虑到驾驶员制动踏板的操作感觉，设计了一种良好踏板感觉分配策略来对后轴制动力矩进行分配，如图5所示。

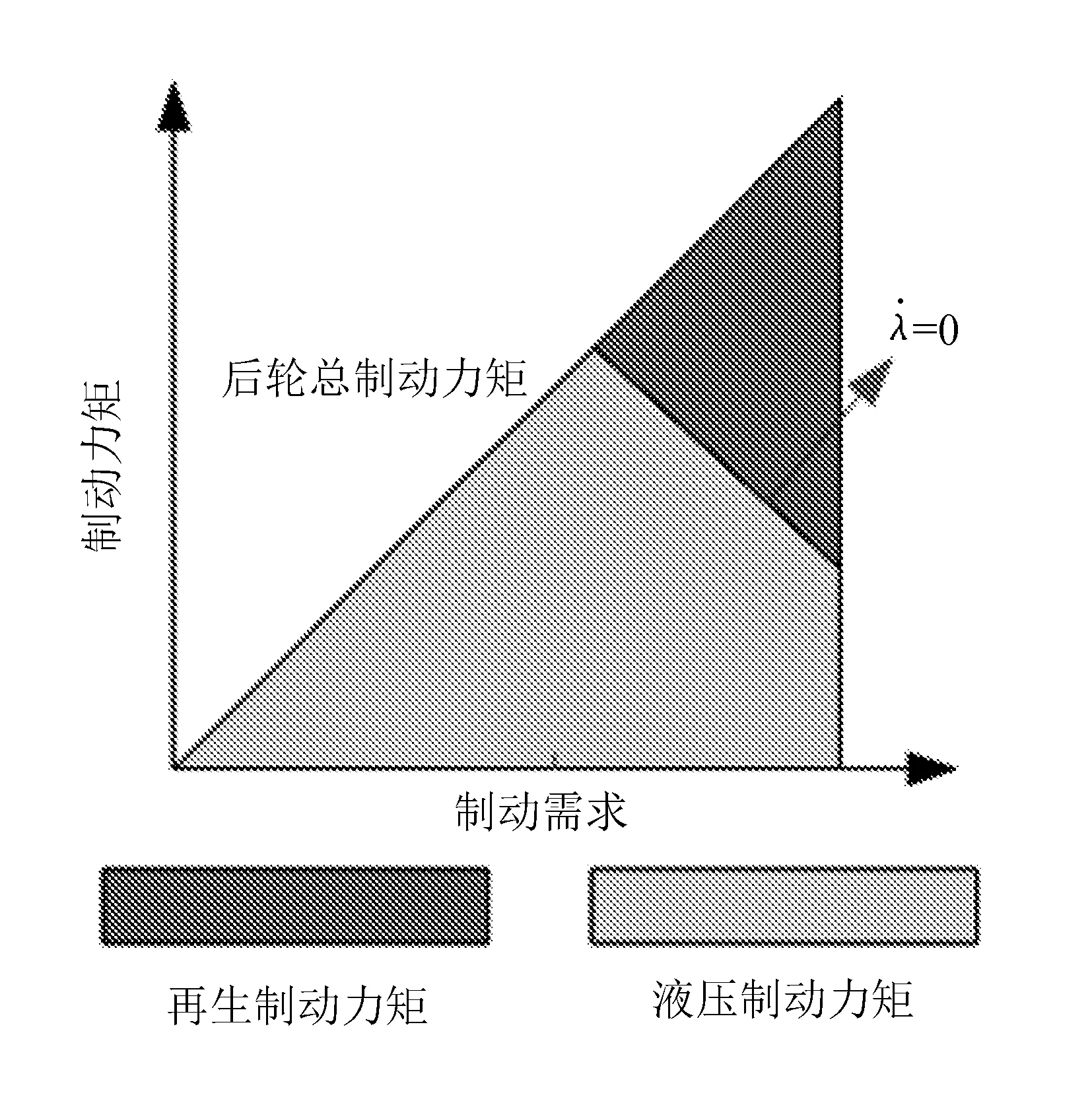
图5 良好踏板感觉分配策略示意图

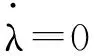
(15)

式中，Fxf和Fxr的大小可由式(7)获取。

4 仿真验证及分析

在MATLAB/Simulink环境下，搭建仿真试验平台对上述分配方法进行仿真研究，汽车整车参数见表2。

取μx=0.8和μx=0.3高、低两种附着路面为工况，分别给定初速度78 km/h和50 km/h。取预测时域P=10，控制时域M=2。

表2 汽车仿真相关参数

路面附着系数估情况如图6所示。

(a) μx=0.8高附着路面估计

(b) μx=0.3低附着路面估计

在仿真初始阶段前0.1 s，路面附着系数估计值有很大的波动，是因为在初始阶段，滑移率从零开始增加，五条μ-λ曲线的间隔较小，甚至重叠。在0.1 s之后路面附着系数估计值不再波动且估计较为准确。

高附着路面工况下汽车制动效果如图7所示。

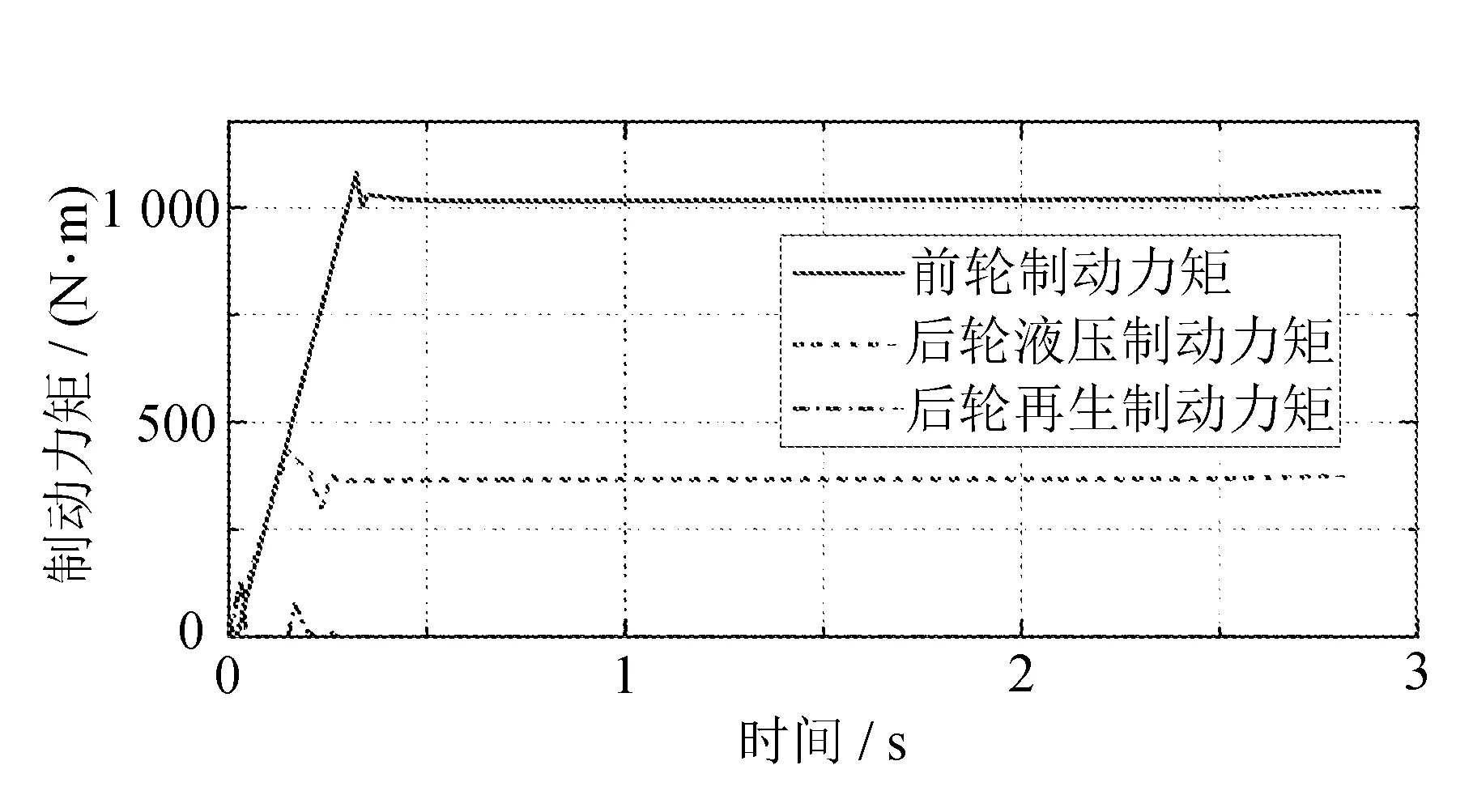
(a) 制动力矩变化图

(b) 滑移率变化图

(c) 电池SOC变化图

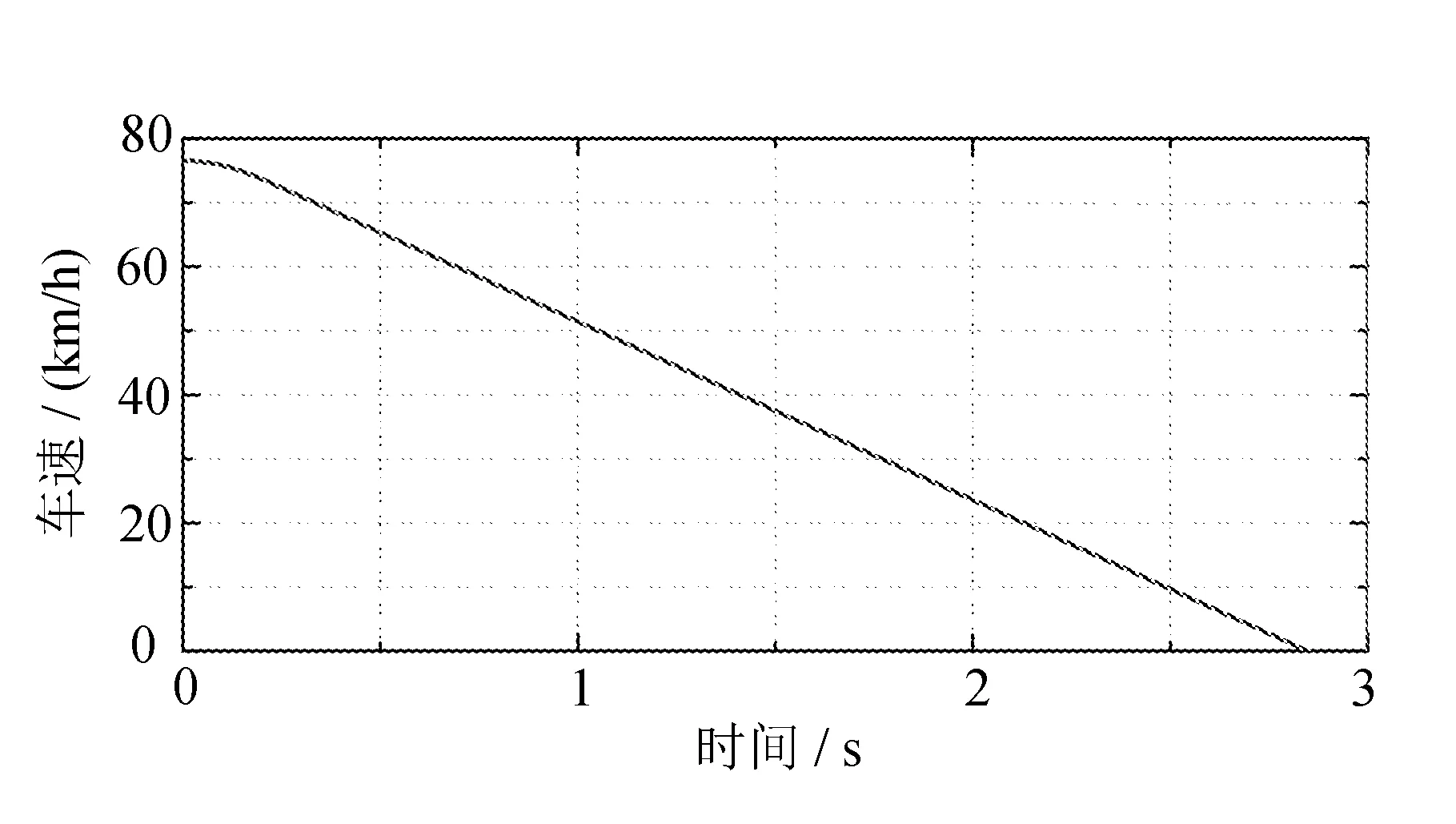
(d) 车速变化图

从图中可以看出:液压制动力矩从零增长到430 N·mm左右之后保持稳定，避免了踏板抖动现象的发生，而再生制动力矩在开始阶段参与制动；滑移率始终稳定地跟踪最佳滑移率，防止了车轮抱死情况；电池SOC也有所增长，说明该分配策略也可以实现能量回收；制动过程为2.8 s。

低附着路面工况下的制动仿真效果如图8所示。

(a) 制动力矩变化图

(b) 滑移率变化图

(c) 电池SOC变化图

(d) 车速变化图

由于是低附着路面，此时的制动时间明显变长，制动力矩较图7减小，但液压制动力矩仍然保持稳定，滑移率跟踪效果也较好。

5 结 语

以后轮驱动电动汽车为对象，针对当前机电复合制动力矩最大化利用及制动踏板抖动等现象，提出了基于模型预测的机电复合制动力矩分配策略。经仿真验证，该策略可以实现制动力矩的最大利用，并能防止车轮抱死，在收获良好制动效果的同时，减少制动踏板抖动现象。

参考文献：

[1] 郭洪强.前后轴独立驱动电动汽车复合制动策略优化研究[D].北京:北京理工大学,2014.

[2] 宋世欣,王庆年,王达.电动轮汽车再生制动系统控制策略[J].吉林大学学报:工学版,2015,45(2):341-346.

[3] Fazeli A, Zeinali M, Khajepour A. Application of adaptive sliding mode control for regenerative braking torque control[J]. IEEE/ASME Transactions on Mechatronics,2012,17(4):745-755.

[4] 王耀南,刘东奇.电动汽车机电复合制动力分配策略研究[J].控制工程,2014,21(3):46-50,55.

[5] 孙晓坤.分布式驱动电动汽车机电复合制动控制策略研究[D].北京:北京理工大学,2015.

[6] Bhandari R, Patil S, Singh R K. Surface prediction and control algorithms for anti-lock brake system[J]. Transp. Res. Part C: Emerg. Technol.,2012,21(1)：181-195.

[7] Wang B. A robust wheel slip ratio control design combining hydraulic and regenerative braking systems for in-wheel-motors-driven electric vehicles[J]. Ournal of the Franklin Institute,2015,352(2):577-602.

[8] Yuan L, Chen H, Ren B, et al. Model predictive slip control for electric vehicle with four in-wheel motors[C]//Control Conference. IEEE,2015:7895-7900.

[9] Zhao H, Ren B, Chen H, et al. Model predictive control allocation for stability improvement of four-wheel drive electric vehicles in critical driving condition[J]. Control Theory & Applications Iet.,2015,9(18):2688-2696.

[10] Ren B, Chen H, Zhao H, et al. MPC-based yaw stability control in in-wheel-motored EV via active front steering and motor torque distribution[J]. Mechatronics,2015,38:103-114.