基于有限元的电液伺服试验机立柱分析与优化

王晓东， 王 龙， 孙 锐， 张 炜

(长春工业大学 机电工程学院， 吉林 长春 130012)

0 引 言

近几年，随着橡胶支座在实际工程中应用越来越广，它的力学性能需要专门设备进行检测，这推动了试验机行业的发展，试验机行业发展越来越快，被大部分领域普遍应用，在国民经济中有很高的地位[1]。人们对它越来越关注，市场需求逐渐增大。现代化试验机系统朝着高精度、大载荷方向发展，大载荷对结构要求较高，试验机设计者往往以经验设计，会造成材料的浪费。这就需要对试验机轻量化进行研究，立柱等关键基础零部件也在向轻量化领域延伸[2-3]。

试验机主体结构大多选用龙门框架结构，立柱作为龙门框架结构的基础零部件，对龙门框架结构的稳定性以及试验机整机结构的稳定性具有重要作用。为了满足整机的性能要求，立柱必须满足动静态要求。文中以立柱轻量化为研究目的，首先对立柱进行模态分析，得到相应的固有频率和振型。再对立柱进行静力分析，得到立柱的最大变形分布和应力分布。在动静态分析的基础上，以单元密度为设计变量，以节点合位移最大化和体积分数最小化为目标函数进行多目标拓扑优化，实现轻量化的目的。

1 电液伺服试验机立柱模型建立

在对立柱进行建模过程中，需要对立柱模型进行简化处理[4-5]。忽略掉一些不重要的小孔、倒角，对立柱结构采用Tetrahedrons[6]网格划分方法，该方法可以提高网格质量，通过尺寸来控制网格大小及网格划分的质量。由于立柱的垂向最大尺寸为2 450 mm，水平最大尺寸为700 mm，模型采用基本尺寸为30 mm的网格划分，共有7 576个节点，23 409个单元。模型、网格分别如图1和图2所示。

图1 立柱三维模型

图2 立柱有限元模型

立柱采用Q345材料，泊松比为0.3，密度为7.86×103kg/m3,立柱质量为6.53 t。

2 立柱的模态分析

在有限元模型的基础上，定义好立柱材料的密度、泊松比和弹性模量，在立柱螺栓孔六个自由度采用完全固定约束。利用有限元软件中的Load Step工况卡片将SPC约束卡片与Eigrl卡片进行加载，通过Radioss求解器对立柱进行模态分析运算，可以判断出立柱结构的动态刚度良好。立柱前四阶模态振型分布如图3所示。

(a) 一阶模态振型

(b) 二阶模态振型

(c) 三阶模态振型

(d) 四阶模态振型

从图3中可知，立柱第一阶固有频率为291.2 Hz,表现为肋板中部绕X轴左右摆动；立柱第二阶固有频率为307.2 Hz，其肋板绕Z轴前后扭动；立柱第三阶固有频率为411.3 Hz，其肋板绕X轴左右扭振；立柱第四阶固有频率为454.1 Hz，其肋板中上部两边绕X轴反向扭振。由于试验过程中所加载的载荷的最大频率为0.05 Hz，综合分析知立柱的动刚度良好。

3 对立柱进行静力分析

在约束静态分析的基础上，对其进行静力分析。对立柱主要作用力为自身所受重力、上横梁的压力、油缸输出载荷对上横梁的反力所引起的扭矩及水平剪切力。将上面所述的力通过OptiStruct的LOAD卡片进行力耦合后来模拟实际工况。受力示意图、仿真效果图分别如图4～图6所示。

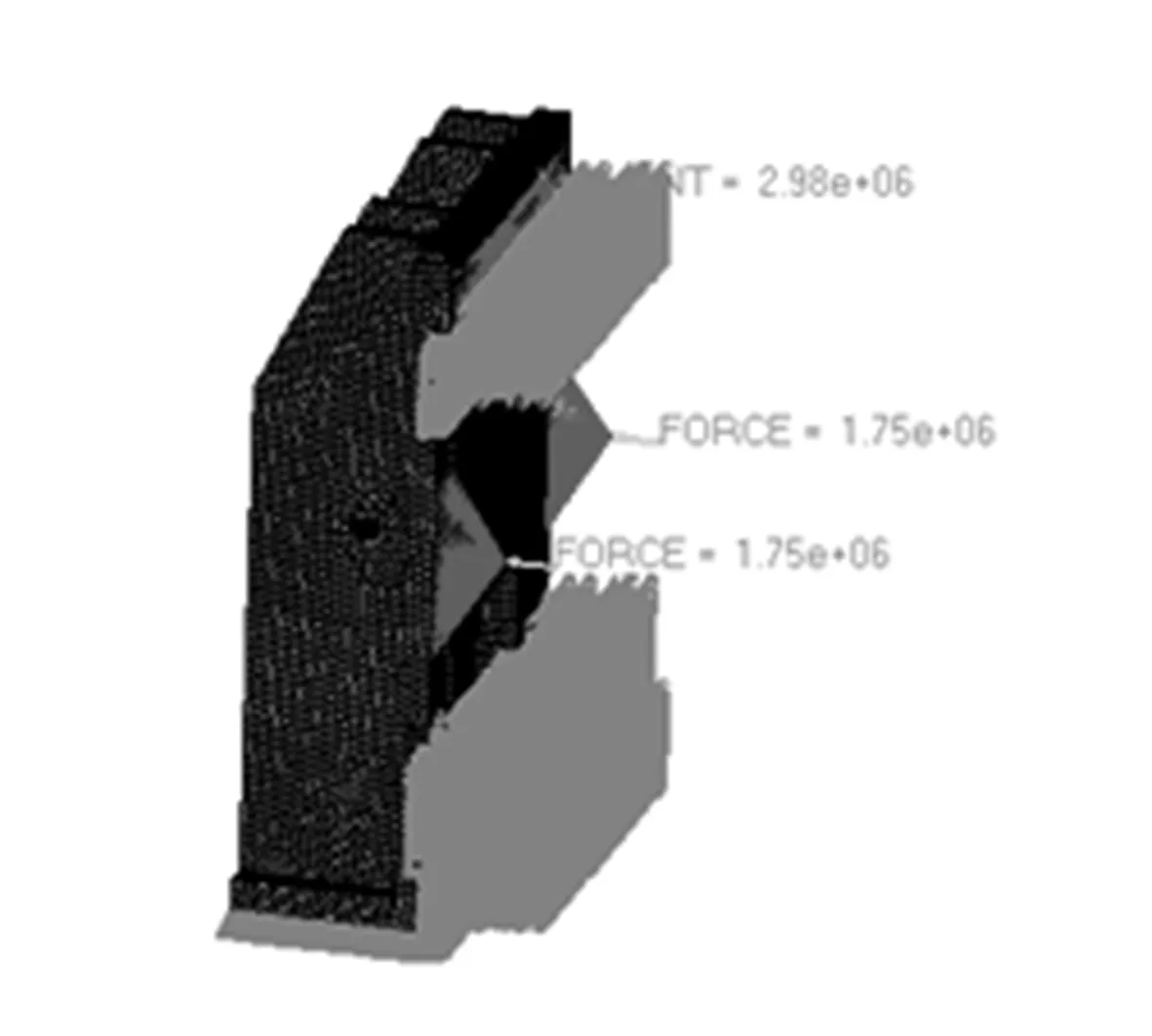
图4 受力分布图

图5 应力分布云图

图6 应变分布云图

由图5可以看出，立柱的总体最大位移为0.309 mm,最大变形主要发生在与滚动滑块接触的部分，小于立柱垂向尺寸的1/2 000～3/2 000[7]，满足设计要求；从图6可以看出，立柱所受最大应力为123.2 MPa，小于立柱选用的材料Q345的屈服极限强度345 MPa。以上分析结果表明，原模型在结构设计方面有很大的优化空间。

4 立柱多目标拓扑优化

立柱结构采用变密度法(SIMP)的多目标拓扑优化[7]：以单元密度为设计变量，以载荷节点合位移和体积百分比0.3为约束条件，目标使立柱结构柔度最小化。拓扑优化的目的是在保证立柱刚度以及一阶固有频率的前提下尽可能减少立柱的设计材料。

运用HyperWorks中的OptiStruct拓扑优化模块对立柱进行拓扑优化，在建立好的有限元模型中创建可设计区域和不可设计区域，与上横梁、油缸支撑架接触的重要部分保留，其余部分为不可设计区域。通过设置相关参数,两者的权重关系为1∶1，定义好立柱材料属性、立柱的优化区域及非优化区域，模型如图7所示。

图7 立柱优化区域图

优化后的迭代曲线如图8～图10所示。

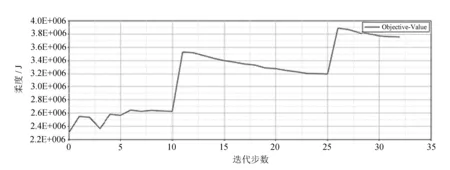
图8 优化目标迭代曲线

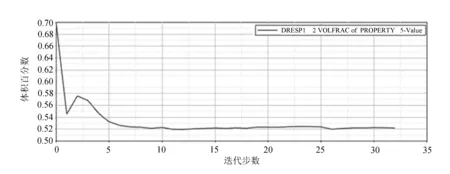
图9 体积百分比迭代曲线

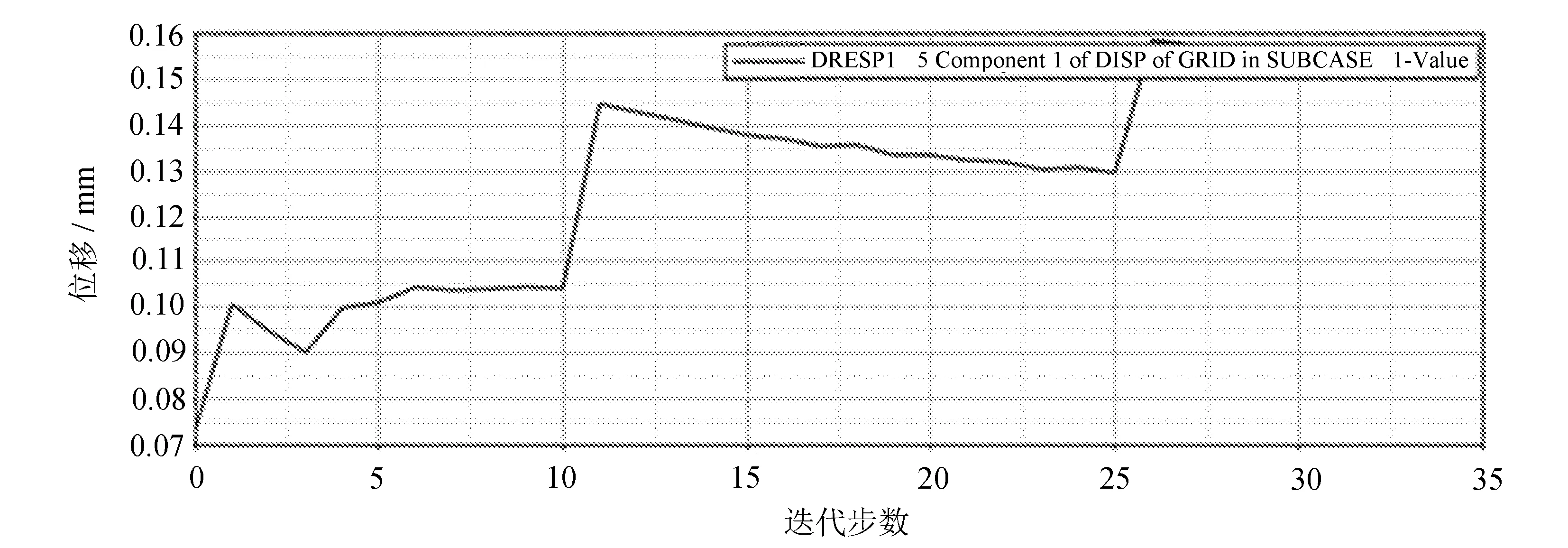
图10 节点载荷合位移迭代曲线

由图8可以看出，立柱的节点载荷合位移经过迭代后到一定值趋于稳定；由图9可知,立柱体积百分比经过迭代后有所下降，在一定值后趋于稳定；由图10可知,拓扑优化目标经过迭代后趋于稳定，表明优化后立柱性能趋于稳定。

立柱的可设计区域材料的最优化布局的等值面如图11所示。

图11 立柱拓扑优化材料分布结果

由立柱拓扑优化材料分布结果可知，立柱中起主要作用的部分需要保留，其他部分需要考虑改进。根据优化后的材料分布情况在CATIA中进行二次改进设计。

根据拓扑优化云图11进行改进，优化后的立柱模型如图12所示。

图12 改进后的三维模型

5 立柱优化结果分析与验证

对改进的立柱进行有限元分析，计算相同工况下的静态特性如图13和图14所示。

图13 应力分布

图14 应变分布

改进的立柱动态特性如图15所示。

(a) 一阶振型

(b) 二阶振型

(c) 三阶振型

(d) 四阶振型

由图13可知,改进后新立柱的应力变形为148.8 MPa，远小于材料的屈服极限应力，安全系数为2.32，符合设计要求。

由图14可知,改进后的立柱应变为0.497 mm，小于立柱垂向尺寸的1/2 000，符合设计要求。

由图15可知,改进后的新立柱一阶固有频率为300.1 Hz,二阶固有频率为321.4 Hz,三阶固有频率为421.3 Hz,四阶固有频率为448.9 Hz。

改进前的质量为6.53 t，改进后的质量为6.1 t，减少了6.58%；一阶固有频率为288.5 Hz，略微降低，变形为0.497 mm，远小于立柱垂向尺寸的1/2 000，满足设计要求。

6 结 语

应用有限元软件HyperMesh对立柱进行模态、静力分析，通过拓扑优化得到最优布局等面图，由等面图对结构进行重新设计。得到新模型的一阶固有频率为288.5 Hz，略微降低。最大变形量为0.497 mm，在设计要求的范围之内。质量减轻了6.58%。结果表明，经过拓扑优化分析，一阶固有频率略降低，模型质量减轻，新的立柱满足设计要求，达到轻量化的目的。

参考文献：

[1] 鲁绍曾.现代计量学概论[M].北京:中国计量出版社,1987.

[2] 官德娟,朵丽霞,陶泽光.机械结构轻量化设计的研究[J].昆明理工大学学报,1997(4):64-69.

[3] 王兴宇.大吨位自卸车轻量化研究[D].武汉:武汉理工大学,2009.

[4] 左越.基于贝叶斯概率抽样和灵敏度分析的有限元模型修正方法[D].武汉：华中科技大学,2016.

[5] 赵俊鹏,姜大伟,高智,等.专用运输车副车架有限元分析[J].长春工业大学学报,2015,36(4):421-425.

[6] 王玮,李自贵,赵海峰,等.全断面掘进机综合试验机刀盘有限元分析[J].机械设计与制造,2013(6):137-140.

[7] 王洪权.万吨级结构试验台机架结构的设计与分析[D].哈尔滨：哈尔滨工业大学,2015.

[8] 冯伟.基于变密度法的箱型梁结构拓扑优化研究[D].太原:中北大学,2014.