基于非下采样Contourlet变换的多模态医学图像融合

程 钢, 李玮琳, 李 丽

(1.长春工业大学人文信息学院 信息工程系， 吉林 长春 130022；2.长春工业大学 机电工程学院, 吉林 长春 130012)

0 引 言

进入21世纪以来，随着时代的进步，医疗水平突飞猛进的发展，医学上出现了多种医学影像成像系统，多模态医学图像的产生，提供了多个角度对同一病变部位不同的医学信息。磁共振成像(Magnetic Resonance Imaging， MRI)有利于显示软组织，可对病灶范围进行分离，但缺少刚性的骨组织作为定位参照。计算机断层扫描技术(Computed Tomography， CT)可以对病变部位进行准确定位，空间分辨率高，有利于显示骨骼特征，不利于对病灶区域软组织病变的突显。磁共振血管成像(Magnetic Resonance Angiography， MRA)的侧重点在于可以更直观显示有关血管的各项属性。图像融合将各种模态的图像信息融合到一起，实现多信息可视化，对医学研究及病灶的治疗都具有广泛的实用价值[1-2]。

小波变换能够对图像实施多尺度、多方向，多分辨率分解，以小波变换理论为基础的图像融合，融合后图像效果更具实用价值，是很多专家学者在医学图像融合方面的研究热点之一。基于小波变换理论的图像融合固然很好，但融合后图像仍有诸多不足，由于小波变换只有三个方向即水平、垂直和对角的分解，缺乏平移不变性，难以凸显图像的边界、轮廓等二维或多维的区别，融合过程中易产生抖动或振铃现象，对融合后效果产生影响。而近几年逐步产生的非下采样Contourlet变换(NSCT)具有多尺度性、多方向性、平移不变性等特点，并且能够减少抖动和振铃现象[3]，更具实际意义。

文中提出了一种基于非下采样Contourlet变换的多模态医学图像融合算法，对原始图像进行非下采样Contourlet分解后，采用区域能量比加权确定低频融合系数；采用平均梯度和局部区域能量两个值来指导高频融合系数。实验结果显示，文中算法对多模态医学图像融合更具实际意义，能更好地继承原始图像信息,且融合后的图像所含信息量更多，细节信息更饱满，是一种更具有实际意义的融合方法[4-5]。

1 基于NSCT的医学图像融合原理

首先对配准好的两幅源图像进行NSCT分解，从而得到各个子带的子图像，形成特有的结构层次；其次再将刚刚得到的各个子带的子图像逐个融合；最后将所得系数做逆变换处理，才能完成图像融合。这样做可以把各个图像的优势更好地进行综合。NSCT图像融合步骤如图1所示。

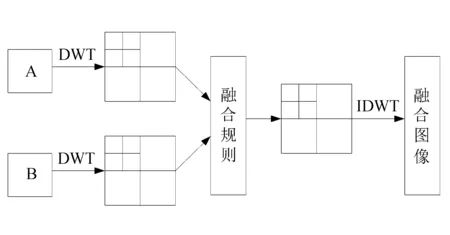
图1 基于NSCT的图像融合过程

2 融合算法

融合方法的准确制定是保证融合图像质量的关键技术，其对融合后效果的影响十分明显，这个技术难点至今仍存在诸多不足[6]。传统研究都热衷于怎样制订高频融合规则，然而低频系数常被忽略，往往直接采取平均法，该方案致使图像边缘特征没有得到足够重视，在很大范围内导致图像不够清晰[7]。文中首先制定低频部分的融合方法，其次再制定高频部分的融合方法，更具实际意义。

2.1 低频子带融合方法

这部分子带能够反映并延续原始图像的大多数特征，所以融合图像的质量受低频系数的影响也很大。局部区域能量能够充分反映出图像的主要结构，随着局部区域能量的增大，源图像所含信息量也逐渐增大。文中提出了独家的基于区域能量比加权的方法来指导低频融合[8]。

选择局部区域能量做参考值的常见低频系数制定方法有局部最大值法和加权平均法。采用局部最大值方法时，当原始图像局部区域值差距较小时易产生选择错误；采用加权平均法时，虽可使融合图像稳定，但对细节特征的处理还有很多不足。文中提出的低频系数选择方案根据源图像局部区域能量的大小,将前两种方法相结合，更多地继承了显著图像的细节信息,让算法的稳定性得到了进一步加强。

将低频分量分解成R×S大小的图像块，文中R×S大小取值3×3，首先对于低频系数CAL和CBL，子带中以(x,y)为中心的局部区域能量为：

(1)

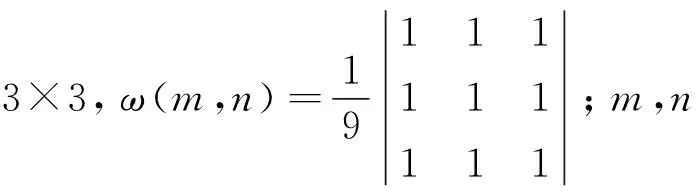
计算两幅图像A,B在该区域内的能量的比值：

(2)

它突显出两图像间的关联。

做两个原始图像的对应图像块间能量的比，再结合加权融合的方法对图像块实施融合处理。设阈值λ(0<λ<1)，一旦两个原始图像A,B局部能量相差悬殊时(R<λ或R>1/λ)，能够得出二者中一个图像所包含的细节信息较为丰富，而另一个图像应该会包含寥寥无几的细节信息，因而融合后的小波系数应选择局部区域能量较大的图像的系数来充当；当局部能量相差无几时(λ≤R<1或1≤R<1/λ)，表示二者包含的细节信息趋近于相等，地位相当，所以用加权平均法获得融合后的小波低频系数更为妥当。一来能够更好地突显出图像中比较明显的部分，二来干扰也得到了有效抑制，为融合的鲁棒性保驾护航[8]。权值w按如下方法计算：

(3)

将w代入公式：

QL=wCAL+(1-w)CBL

(4)

式中:QL----融合图像的低频子带系数。

2.2 高频子带融合方法

这部分子带能够突显出图像的亮度变化特征，尤其是图像的边界及边缘之地等。众多高频子带融合方法要么是针对像素的融合方法，要么是针对窗口的融合方法。然而图像的局部特征并不能只取单个像素的变换系数来表现，应该取某个局部区域的多个像素的图像变换系数综合体现。所以，很多种融合算法都是针对窗口进行的。诸多被选择的局部特征例如基于能量的以及基于方差的。在所选择的窗口中，直方图上突现变化的地方，能够看出此处灰度级跳跃性大，所包含细节信息涵盖量更大。

平均梯度不仅能够突显出细节之处反差的大小，还能够突显图像的纹理细节变换。一般来说，其值越大，预示层次越丰富，层次较多的时候图像所具有的清晰度越好。平均梯度是一个出现频率较高的图像融合质量评价指标，一般来说，用于评价图像在细节及纹理表现方面的好坏。文中将平均梯度、局部区域能量相结合，综合衡量来实施高频部分的融合。

首先对于高频系数CAH和CBH，局部区域能量为：

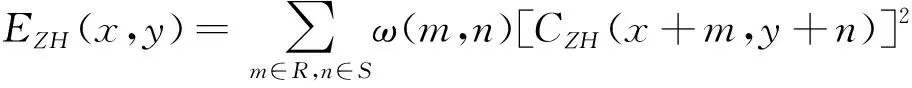
(5)

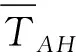
(6)

式中:F(i,j)----图像高频分量分解后K×L大小的图像块中第i行第j列的灰度值。

对高频系数的确立，按照如下方案进行选择：

(7)

高低频系数都确定好之后再进行图像重构。

3 实验效果图及实验数据

一位患者大脑的CT图像和他脑部同一位置区域的MRI图像如图2所示(已完成前期配准)。

(e) 高低频均用文中方法融合

图2(a)突显出骨组织方位；图2(b)突显出软组织结构；若低频用传统简单的加权平均法，而高频部分用文中提出的新的融合规则实施图像融合就可以得到图2(c)；若低频部分系数选择文中提出的新的方法进行图像融合，而高频部分选择简单传统的局部区域能量取大的方法实施融合就能够得到图2(d)[9]；若高低频融合规则均采用文中所提融合方法实施图像融合则得到的是图2(e)。需要说明的是，在图像融合实施过程中均采用Daubechies小波，且选择的都是其中的DB4小波基，而且融合前把两个原始图像都进行三层分解。

我们用肉眼能够看出图2(e)效果更好。

已配准的患者颅脑部位的MRA及MRI图像如图3所示。

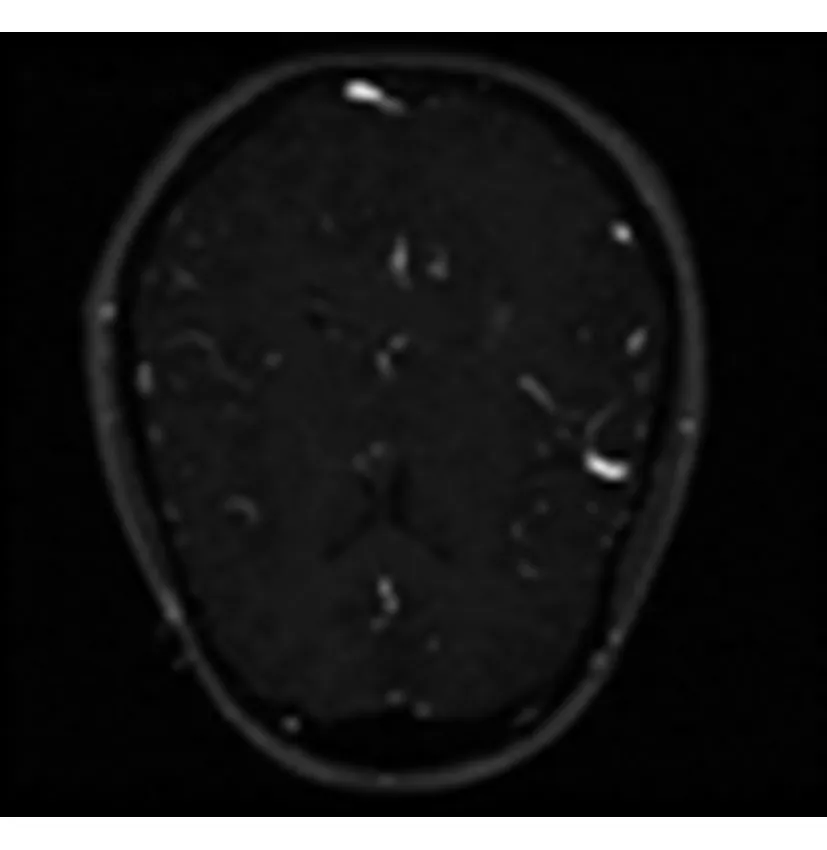
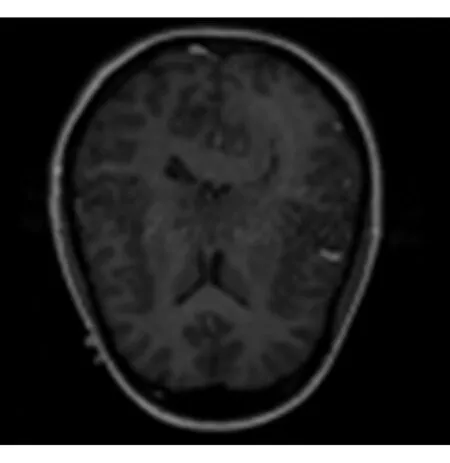
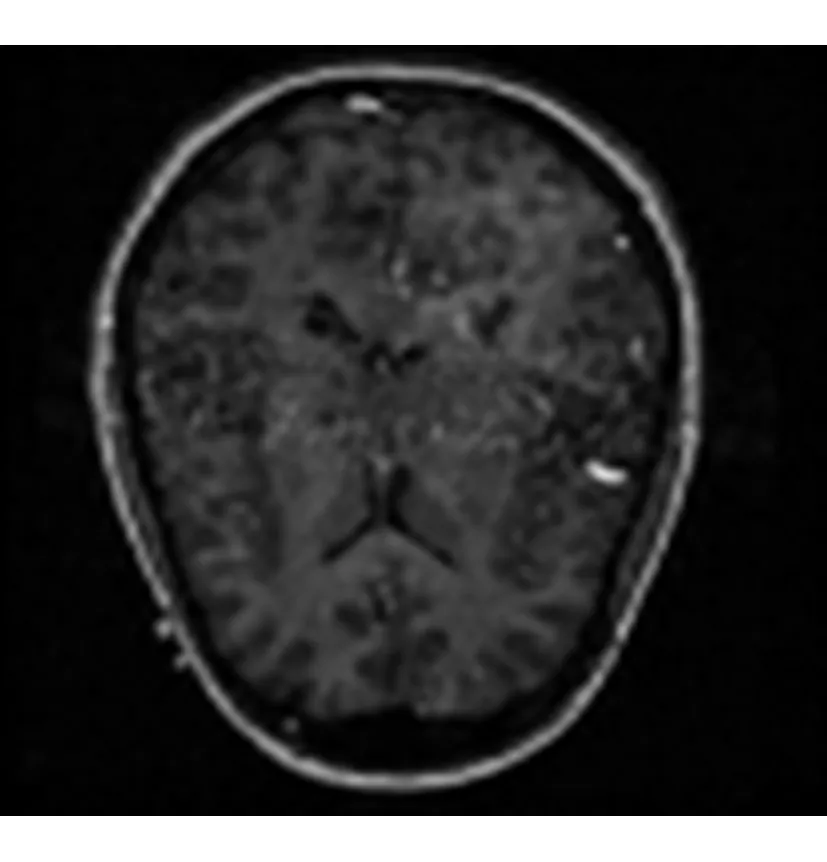
(e) 高低频均用文中方法融合

图3(a)有利于脑部血管组织的显示；图3(b)能够突显软组织的结构特征。图3(c)、(d)分别为和图2(c)、(d)采用相同的融合规则实施的颅脑部位的MRA及MRI图像融合。若高低频系数均用文中提出的新的融合规则实施融合后得到的即为图3(e)。

我们用肉眼就可以看出，对图2中一系列结果而言，高低频系数都用文中提出的新方法，实施图像融合后得到的效果图2(e)对骨密度及软组织的成像均比较清晰, 较传统融合算法相比较，效果更理想。而图3(c)、(d)、(e)相比，也只有图3(e)对于血管和脑灰质的显示最为清晰。

我们用三个常见的评价指标来将两组实验图像中得到的结果图实施客观评价，即分别计算其平均梯度、标准差和互信息。平均梯度与图像清晰度有关,并能表现细节信息及纹理特征，平均梯度越大，能够突显出图像层次越多，层次较多的时候图像所具有的清晰度越好；标准差能突显出灰度的统计特征，即灰度离散情况，其值越大表示灰度级分布越不集中，各个灰度级出现的概率差别不大，这时候表示所含的信息量越多；最后一个指标互信息也常用来评价图像融合的客观质量，互信息越大，突显出从原始图像继承和延续的有用信息越多，融合离理想目标更近。以下数据进行对比分析，文中阐述的新的规则实施的图像融合，效果更占上风。

图2和图3的客观评价分别见表1和表2。

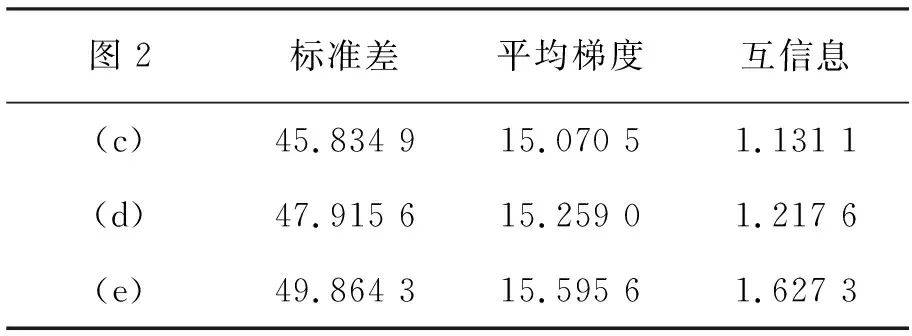
表1 图2的客观评价

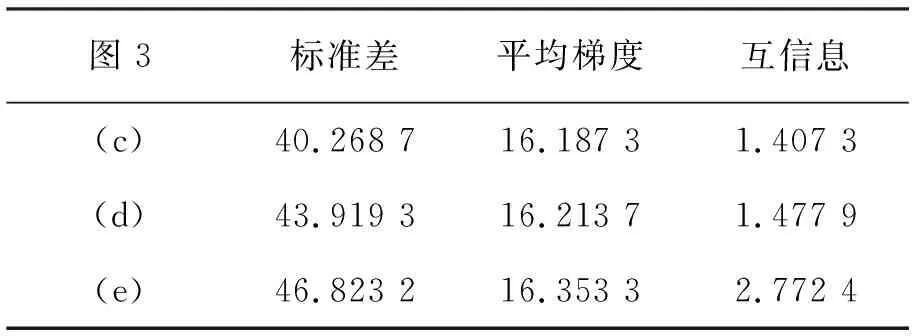
表2 图3的客观评价

从表1综合衡量，图2(e)效果更理想。从表2综合衡量，图3(e)效果更理想。

4 结 语

医学图像融合在医学研究中的重要地位及意义我们毋庸置疑。经过大量研究提出了一种基于非下采样Contourlet变换的多模态医学图像融合算法,分别对低频及高频部分融合规则提出自己独到的见解和想法,并与简单的传统的融合方法例如局部最大值法以及加权平均法进行了实验、图像比对及数据分析。从肉眼观察到实际数据论证, 都能突显出文中提出的图像融合新方法比传统的小波融合方法更具优势。更好地继承了原始图像的边缘信息及细节，为疾病诊断提供更便捷、更有效的依据。

参考文献：

[1] 罗述谦.医学图像处理与分析[M].北京:科学出版社,2010.

[2] 潘树伟.基于多尺度分析的医学图像融合算法研究[D].杭州:浙江理工大学，2017.

[3] 杨艳春，王晓明，党建武,等.基于非下采样Contourlet变换的医学图像融合方法[J]. 计算机科学，2013,40(3):310-313.

[4] 王昕，李玮琳，刘富.小波域CT/MRI医学图像融合新方法[J].吉林大学学报：工学版，2013(s1):34-37.

[5] 宋瑞霞，王孟，王小春，等.基于多层次多方向分解的医学图像融合算法[J].计算机工程，2017(10):179-185.

[6] 徐春艳.基于多尺度分解的医学图像融合研究[D].镇江:江苏大学，2017.

[7] 李玮琳.平移不变小波医学图像融合方法[J].长春工业大学学报:自然科学版，2013,34(6)：653-655.

[8] Lei Wang, Bin Li, Lianfang Tian. Multi-modal medical image fusion using the inter-scale and intra-scale dependencies between image shift-invariant shearlet coefficients[J]. Information Fusion,2012,19:20-28.

[9] 高清河，刚晶，王和禹，等.基于小波变换的多模态医学图像的融合及性能评价[J].生物医学工程研究，2014,33(4):259-263