基于MPC的重型液罐车侧向稳定性控制仿真
于志新, 程新新, 李 杰, 李绍松
(1.长春工业大学 机电工程学院, 吉林 长春 130012;2长春工业大学 汽车工程研究院, 吉林 长春 130012)
0 引 言
我国公路运输线四通八达,各种油品、危化品主要依靠半挂液罐车运输,液罐车具有装载量大、运输成本低的特点,逐渐成为公路运输的主体。因其具有载量大、重心高、轮距相对较小等特点,并且在转向或变道过程中罐内液体易受激励产生晃动,与车体的耦合运动会导致车辆发生侧倾失稳,这在道路运输是极其危险的状况。国内外学者针对罐车侧倾问题在罐内液体晃动分析和罐内结构优化上做了大量研究[1-6],但液体的晃动对整车的侧向稳定性分析相对较少。因此,通过对罐车实施主动安全控制,提高液罐车的稳定性是一种更适用和高效的方法[7-11]。
1 液体晃动分析
以某专用汽车制造厂生产的44 m3半挂液罐车为分析对象,考虑到罐体长度相对较长,忽略罐车两端封头以及内部附加结构影响,并且罐车在平直路面上转弯或避障时,罐体内的轴向运动视为不变,因此选取单位长度上罐体进行建模分析,并作如下假设:
1)液体为理想不可压缩的;
2)不考虑罐内气体的影响;
3)不考虑罐体的变形。
罐内液体坐标系如图1所示。

图1 罐内液体坐标系
图中:x----车辆行驶方向;
y----驾驶员左侧;
z----竖直向上;
Ω----流体域;
Σ----罐体湿表面;
S----自由面液度;
h0----液面到x轴距离;
θ0----自由液面和罐体交点与坐标原点连线同z负半轴的夹角。
液体在罐内的运动方程满足以下三个条件:
1)在Ω内连续;
2)在Σ内不可渗透;
3)在S上满足运动学和动力学条件。
得到以下方程:
(1)
流体势函数分解为液体随罐体运动而产生的刚性分量φu(r,θ,t)以及液体晃动产生的动压力分量φs(r,θ,t)两个子函数和的形式[12]:
φ=φs(r,θ,t)+φu(r,θ,t)
(2)
其中,φu(r,θ,t)和φs(r,θ,t)都满足式(1),可以得到
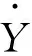
液体自由晃动时,令
φ=iσΦ(r,θ)eiσt
η=H(r,θ)eiσt
则式(1)可化为:
(3)
式中:Φ----晃动模态函数;
H----波高模态函数;
ω----液体自由晃动特征频率。
运用Galerkin法求出上式中的ω和Φ。
当罐体中的液体被动晃动时,自由晃动模型同样适用于受迫晃动。
令φ、η为自由晃动特征模态Φ、H的线性组合,即:
(4)
式中:qi(t)----广义坐标。
将式(4)代入式(1)中,并消去η得
(5)
对上式同乘ρHi,然后在S上作积分,便可得到以下的积分形式:

(6)
其中
液体晃动时,前面已假设液体为理想的不可压缩的流体,忽略了液体之间的相互作用力。但实际上液体之间还有一定的阻尼作用,且无法忽略,于是为简化计算,可在方程中加入比例阻尼项,即:
C=∂0M+∂1K
(7)
其中,∂0,∂1为常数。式(6)变为

(8)
满足精度要求的条件下,截取式(8)一定阶数的近似计算。求解qi(t),即可得到
(9)
2 液体侧向晃动力影响分析
2.1 侧向晃动受力分析
液体之间存在流体力和流体势,根据两者之间函数关系可解出与液体对罐车内壁上的力。流体压强为:
式中:z′----自由液面到所求点的垂直距离。
对单位长度上的静、动压力在罐体长度上积分得到罐体的惯性力Fu、动压力Fs:

(10)
则作用在罐体上的侧向合力为:
(11)
其中
Gi=ρ21-iR1-iZiL
2.2 充液比对液体晃动的影响
液罐车罐内液体与罐体参数如下:
1)液体密度:ρ=580 kg/m3;
2)罐体半径:R=1.5 m;
3)罐体长度:L=12 m。
充液比λ为液体高度与罐体半径的比,截取式(8)的前四阶,计算出在不同充液比下罐体受液体惯性作用力Fu、液体晃动作用力Fs以及两者的合力Fh。侧向受力随充液比的变化如图2所示。

图2 侧向受力随充液比的变化图
由图2可知,在λ∈[0,1]内,充液比与惯性力之间呈线性关系,逐渐升高。惯性力在λ=1时达到最大值;在图中晃动力如同惯性力一样呈现出先增大后减小的趋势;而二者的合力在充液比小时与晃动力表现出相同的变化趋势,并在充液比λ=1.5时,因惯性力作用越来越明显,合力反而表现出不减反增的趋势,但未超过晃动最为剧烈时的最大值。
2.3 侧向加速度对液体晃动的影响
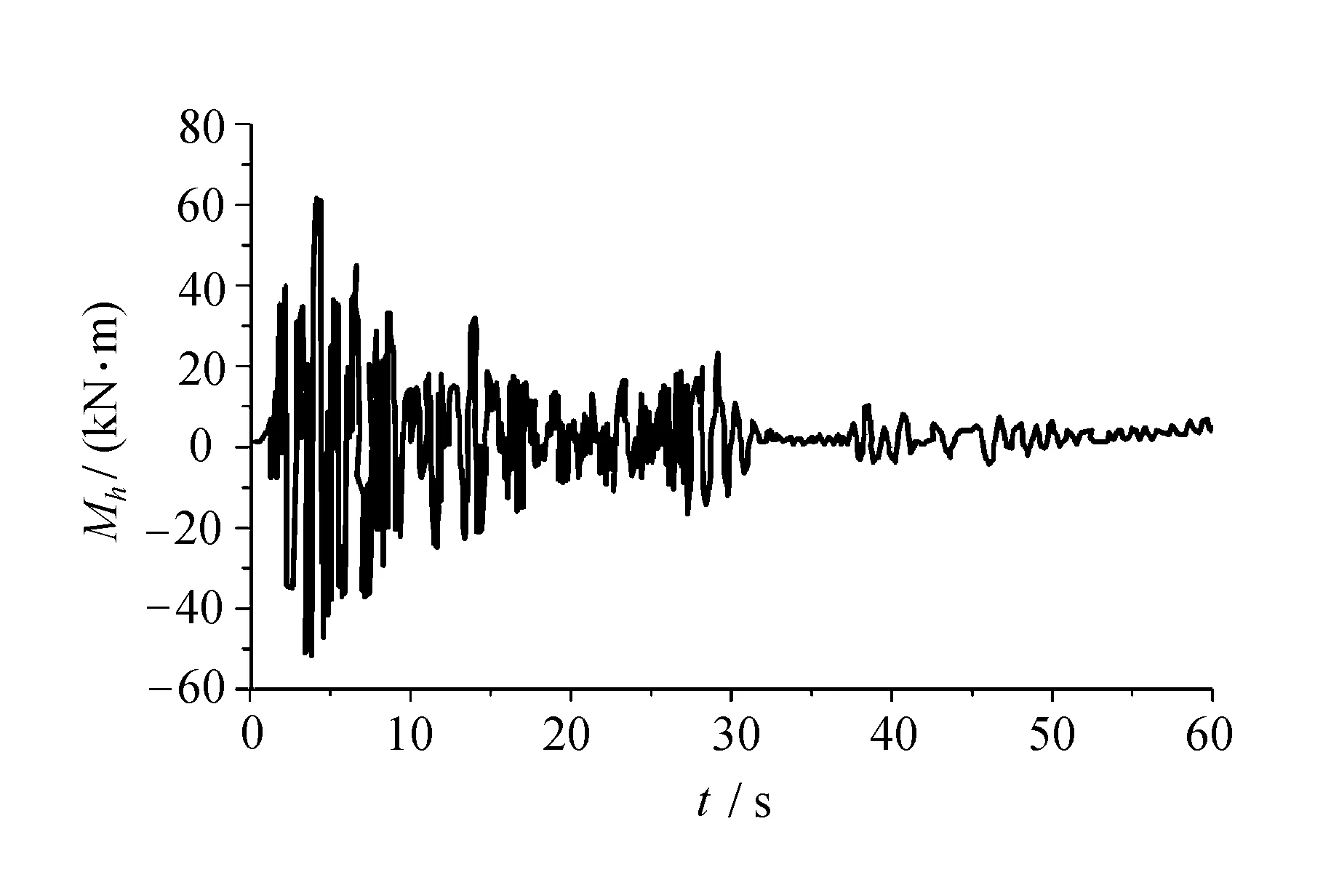
液罐车侧向受力不仅受充液比的影响,而且还受侧向加速度的影响。在此选取充液比λ=1,以埃尔森特罗EI地震波为激励,计算液罐车受到的惯性力矩、晃动力矩和合力矩。侧向加速度激励如图3所示。

图3 侧向加速度激励图
液罐车所受到的惯性力矩、晃动力矩和合力矩如图4所示。
从图4中可知,在λ=1条件下,惯性力矩与晃动力矩的幅值相同时,罐体受到剧烈的晃动,此时罐体极易表现出侧向不稳定,有侧翻的危险。

(a) 惯性力矩

(b) 晃动力矩
(c) 合力矩
但由于惯性力矩和晃动力矩的相位不同,即两者之间的相互作用并不是代数相加,它在实际运动中与很多因素相关。因此,在实际的运动过程中应尽量避免在此类工况下行驶。
3 液体晃动对车辆运动状态的影响
由于液罐车质量和体积较大,若进行实车实验危险过大。在此应用仿真方法分析液体晃动对液罐车稳定性的影响。对比相同的工况下,罐内等质量的固体与液体的运动分别对液罐车稳定性的影响。液体晃动对罐车稳定性影响流程如图5所示。

图5 液体晃动对罐车稳定性影响流程图
仿真液罐车的几个重要参数:
1)充液比λ=1;
2)车速v=40 km/h;
3)角阶跃输入方向盘转角如图6所示。

图6 角阶跃输入方向盘转角
分别对一定质量的液体和等效质量的固体进行仿真,可得到稳定性仿真曲线如图7所示。
图7表明,在角阶跃输入下,与等效质量的固体相比,液体对液罐车稳定性的影响最大。这是因为液体的晃动增加了整体受力的不均匀,使得整车动力稳定性变差。

(a) 侧倾角

(b) 横摆角速度
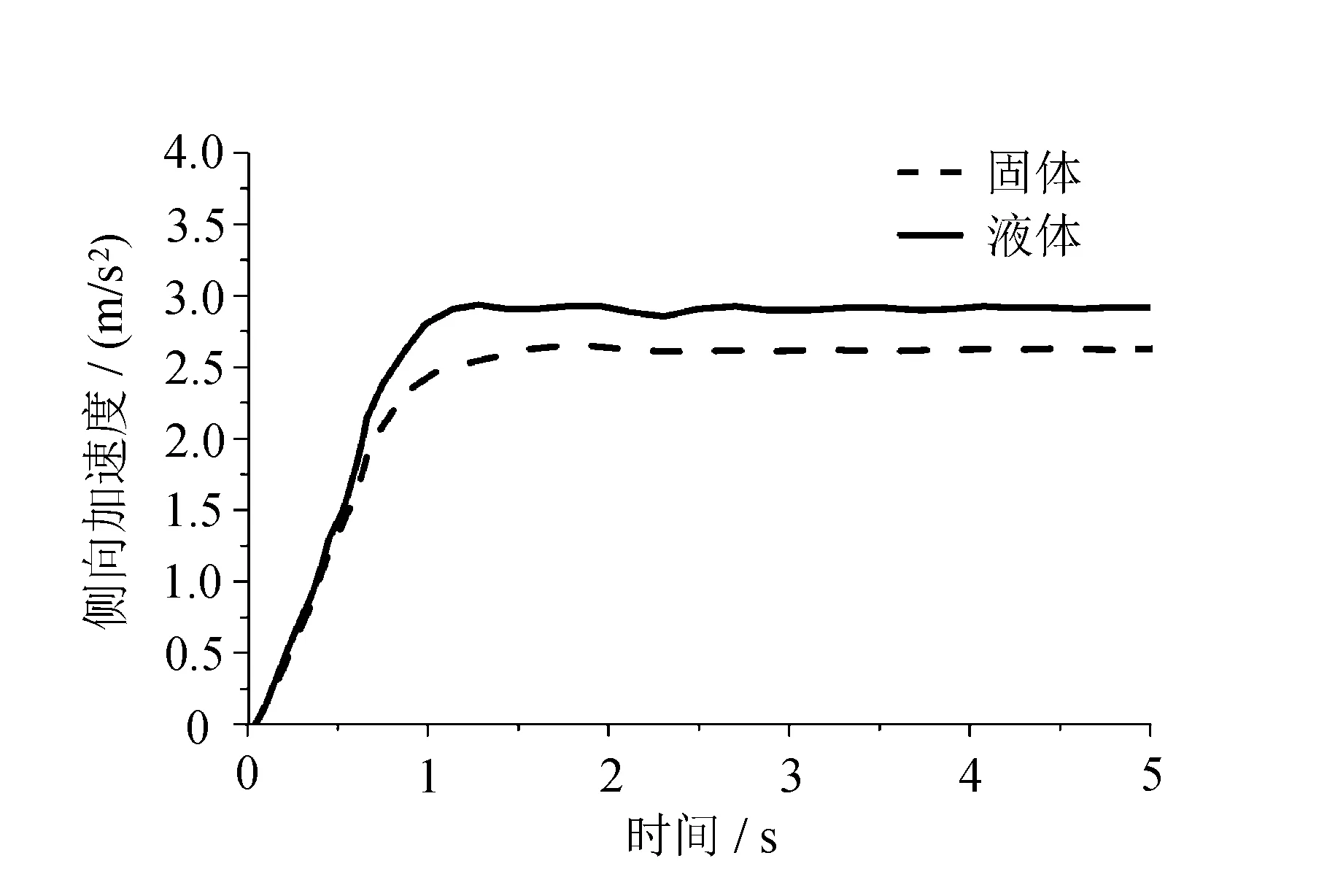
(c) 侧向加速度
4 半挂液罐车动力学模型
考虑整车的侧向、横摆运动及侧倾运动,采用三自由度车辆简化模型,如图8所示。

(a) 横摆
牵引车运动方程
(12)

(13)

(14)
半挂车运动方程
(15)

(16)

(17)
两刚体运动约束方程
(18)
文中采用线性轮胎模型,则有:
(19)
式中:m1,m2----分别为牵引车、半挂车质量;
β1,β2----分别为牵引车、半挂车的质心侧偏角;
ψ1,ψ2----分别为牵引车、半挂车的质心横摆角;
m1s,m2s----分别为牵引车和半挂车的簧载质量;
Fi----第i轮的侧向力;
F4----半挂车对牵引车的作用力;
Φ1,Φ2----分别为牵引车、半挂车簧载质量侧倾角;
I1xx,I2xx----分别为牵引车、半挂车簧载质量侧倾转动惯量;
I1zz,I2zz----分别为牵引车、半挂车横摆转动惯量;
u1,u2----分别为牵引车、半挂车行驶车速;
kr1,kr2----分别为牵引车、半挂车侧倾刚度;
c1,c2----分别为牵引车、半挂车侧倾角阻尼;
k12----第五轮侧倾刚度;
h1c,h2c----分别为牵引车、半挂车质心高度;
h1,h2----分别为牵引车、半挂车质心到各自侧倾轴线的距离;
Γ----铰接角;
a,b,c----分别为牵引车重心到前轴、后轴、铰接点的距离;
d,e----分别为半挂车重心到后轴、前轴的距离。
5 集成模型预测控制器设计
实际的期望质心侧偏角和横摆角速度可以作为模型预测控制器的输入,该控制器的输出为附加的横摆力矩和前轮转角。
为了获得侧向稳定性,实际的横摆角速度应接近期望的横摆角速度。文中设计了三自由度整车模型。整车模型状态空间方程如下:
(20)
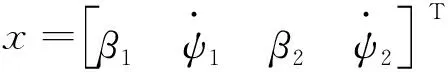
则有:
实际中为保证侧向和侧倾的稳定性,横摆角速度和质心侧偏角都应当被限制在稳定阈值内。期望的横摆角速度可通过稳定参考模型得到:
(21)
式中:
此外,期望的横摆角速度应受到路面附着系数的约束:
(22)
稳态转向时,文中假设牵引车与挂车期望的横摆角速度相同,即
ψ1ref=ψ2ref
为了阻止转向过程中整车的侧倾,期望的质心侧偏角可选为零,即
β1ref=β2ref=0
整车状态空间模型离散化得到如下简约模型:
x(k+1)=F(x(k),u(k))
y(k)=Gx(k)
(23)
在k时刻的车辆状态,依据上述公式可以预测接下来Np步的动力学状态,表述如下:
x(k+Np)=F(x(k),u(k),u(k+1),…,
u(k+Nu),…,u(k+Np-1))
式中:Nu----控制时域;
Np----预测时域。
由文献[13]可知,前轮主动转向电机的控制周期为10~30 ms,没有ABS的液压制动系统的移动周期为20~50 ms,考虑到采样周期应同时满足上述两个条件,即文中采用的采样时间Ts=20 ms,当采样时间超过控制时域,假设控制输入到预测时域之间保持不变,即为:
u(k+Nu-1)=u(k+Nu)=
u(k+Nu+1)=
…=
u(k+Np-1)
在k时刻的最优控制序列U(k)和响应的预测输出为:
其中,y(k+i|k),i=1,2,…,Np,可由式(23)得出。
考虑到控制的要求为实际横摆角速度与期望横摆角速度相匹配。期望横摆角速度公式如下:

控制罐车稳定性所需要的额外横摆力矩是由执行器(制动器的差动制动)而来,为了防止罐车侧翻,该额外横摆力矩应有如下约束:
(24)
此外由于汽车结构的限制,罐车的前轮转向角度也有一定的约束范围:
δmin≤δ(k)≤δmax
(25)
当罐车进入弯道或变道时,其实际横摆角速度应很快与期望的横摆角速度匹配,于是使目标函数J1=‖(Y(k+1|k)-R(k+1))‖2值最小。此外,为了使输入平稳顺滑,目标函数J2=‖U(k)‖2值也应最小。于是联立J1,J2就可得到整车控制的目标函数:
J(Y(k),U(k),Nu,Np)=‖Qy(Y(k+1|k)-R(k+1))‖2+‖QuU(k)‖2
(26)
式中:Qy,Qu----权重矩阵。
为了得到上述目标函数的最优解,就要基于约束条件式(24)、式(25)求解。
当得到最优控制序列U(k),选取k时刻最优控制序列中的第一个值作为k+1时刻的输入。然后整个预测时域向前移动一个间隔,在重复滚动优化得到此后的最优控制值。模型控制框图如图9所示。
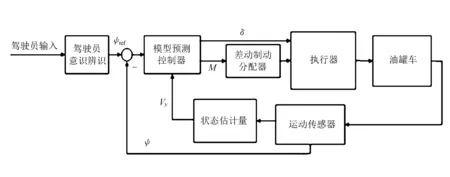
图9 液罐车稳定性控制框图
6 仿真结果分析
为了验证控制策略的有效性,选择极限条件下的鱼钩工况进行仿真,在该工况下,液罐车的失稳基本表现为侧翻事故。针对液体晃动降低液罐车行驶稳定性,以三自由度半挂液罐车为参考模型,采用模型预测控制计算出最优的附加横摆力矩,制定差动制动的控制方案来分配附加横摆力矩,经仿真分析对比得出液罐车侧倾角、横摆角速度、侧向加速度曲线如图10所示。

(a) 方向盘角输入

(b) 侧倾角

(c) 横摆角速度

(d) 侧向加速度
由图(10)可以看出,未施加控制的半挂液罐车侧倾角会出现急剧的变化,侧向加速度超过重型车辆的侧翻阈值0.4 g,施加控制的液罐车侧向加速度稳定在0.3 g内,未施加控制的液罐车比有控制的侧向加速和横摆角速度跳动的幅度范围更大。在7.5 s时未施加控制的液罐车侧倾角发散,此时车辆已经发生侧翻,而施加控制后液罐车侧倾角收敛,始终在稳定阈值内。
7 结 语
1)根据势流理论建立了液罐车罐体内液体的运动方程,分析了液体晃动特性和影响因素。在λ=1时,液体晃动最剧烈。
2)为研究液体晃动对液罐车稳定性的影响,在角阶跃输入下进行装载固液货物对比仿真试验,试验表明,与装载固体货物相比,液罐车的侧倾角和横摆角出现较大的变化,液体的晃动对整车稳定性影响较大。
3)在极限工况下仿真分析结果表明,设计的模型预测控制策略能够有效地提高车辆行驶稳定性。
参考文献:
[1] Welt F, Modi V J. Vibration damping through liquid sloshing, Part Ⅰ: A nonlinear analysis[J]. ASME Transactions, Journal of Vibration and Acoustics,1992,114(1):10-16.
[2] Chen C, Tomizuka M. Lateral control of commercial heavy vehicle[J]. International Journal of Vehicle Mechanics and Mobility,2000,33(6):391-420.
[3] Yan G R, Subhash Rakheja, Siddiqui K. Analysis of transient fluid slosh in partly-filled tanks with and without baffles: Part 1:Model validation[J]. International Journal of Heavy Vehicle Systems. 2010,17(3):359 -379.
[4] Iman Hazrati Ashtiani, Mehrnoosh Abedi. Effects of Liquid Cargo on Lateral Stability of B-Train Combination[C]//SAE Technical Paper,2014-01-2319.
[5] 岳宝增,祝乐梅,于丹.储液罐动力学与控制研究进展[J].力学进展,2011,41(1):79-91.
[6] 赵树恩,赵灵鹤.汽车罐车横向运动液体晃动动力学特性模拟[J].应用数学和力学,2014,35(11):1259-1270.
[7] Avesta Goodarzi. Integrated Yaw and Roll Moments Control of Articulated Vehicles[C]//SAE Paper,2009-01-2874.
[8] Ji Y, Guo H Y, Chen H, et al. Integrated control of active front steering and direct yaw moment based on model predictive control[C]//6th chin. Control Decis. Conf. Changsha, China,2014,34(2):2044-2049.
[9] Jianbo Lu, David Messih. An enhancement to an electronic stability control system to include a rollovercontrol function[C]//SAE Paper,2007-01-0809.
[10] 于志新,宗长富.基于LQR的重型半挂汽车列车稳定性控制策略[J].中国公路学报,2011,24(2):114-119.
[11] 赵伟强,封冉,宗长富.基于等效晃动模型的液罐车防侧翻控制策略[J].吉林大学学报:工学版,2018,48(1):30-35.
[12] 卢军.任意充液比油罐车液体晃动及整车横向稳定性研究[D].成都:西南交通大学,2009.
[13] Bing Zhu, Qi Piao, Jian Zhao, et al. Integrated chassis control for vehicle rollover prevention with neural network time-to-rollover warning metrics[J]. Advances in Mechanical Engineering,2016,8(2):1-13.

