模糊控制和HYDRUS-2D在农业浇灌中的应用

李奇涵， 郭雪强， 郗 元

(1.长春工业大学 机电工程学院， 吉林 长春 130012；2.大连理工大学 盘锦产业技术研究院， 辽宁 盘锦 124221；3.吉林大学 机械科学与工程学院， 吉林 长春 130022)

0 引 言

掌握土壤水分的运动规律对改进灌溉技术、合理利用水资源以及提高作物产量具有重要意义。冀荣华等[1]利用HYDRUS-2D对所建模型求解，所建模型可以有效描述负压地下灌溉条件下土壤水分入渗规律,并和实际试验相互验证。莫彦等[2]通过两年田间试验分析了地下滴灌玉米出苗率与灌水后种子处土壤有效饱和度的关系,并基于HYDRUS-2D构建了地下滴灌开沟播种土壤水分运动模型。Mark Bloomberg等[3]利用HYDRUS建立生长反应模型，模拟我国华北平原上成熟的三倍体种属植物的土壤水分利用。

以上研究成果为分析土壤水分运动的模拟提供了很好的依据。研究发现，目前使用HYDRUS-2D进行模拟的主要是传统控制的浇灌方法，而在智能控制浇灌方法中通常采用直接试验方法获得数据，来调整模糊控制的隶属度函数，由于在农田浇灌中水分变化的复杂性和超滞后性，导致数据获取难度大且非常耗时[4]。所以文中主要针对土壤水分入渗的复杂性和超滞后性，以黄瓜生长期最适土壤含水量为目标，通过使用HYDRUS-2D建立土壤水分运移模型求解快速获得仿真数据，来调整模糊控制算法的隶属度函数。

1 试验材料

本试验选用中国各地夏季主要菜蔬之一黄瓜作为实验材料。根据文献[5]提取出黄瓜在成长期的最适土壤质量含水量为0.210～0.315,土壤相对含水量为60%～90%。

选取长春地区田间栽培用土壤作为HYDRUS-2D的土壤组成，用环刀法取土样，测定土壤颗粒组成(用马尔文激光粒度仪测定)和土壤容重，见表1。

表1 土壤的物理颗粒组成及容重

2 HYDRUS土壤水分运移模型建立

2.1 模型建立原理

模型模拟地面滴灌过程，滴头间距远小于滴灌带铺设间距时，地面滴灌属于面源入渗，即轴对称三维入渗。相应坐标系下的Richards方程为：

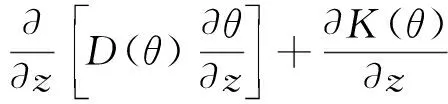
(1)

在假定土壤均匀、稳定并且土壤水的密度恒定条件下，可以简化为一维垂直入渗，方程为：

(2)

式中：θ----土壤体积含水率，cm3/cm3；

t----时间，min；

D(θ)----土壤水扩散率，cm3/cm3；

K(θ)----非饱和土壤导水率，cm/min；

x，y，z----坐标轴中方向坐标，cm。

HYDRUS-2D采用流体建模有限元分析模拟土壤水分入渗过程以及监测点土壤水含量信息。根据文中研究目标，使用Van Genuchten模型更适合模拟研究没有作物情况下的土壤水分运移过程试验[6-7]。通过使用Van Genuchten模型，利用HYDRUS-2D中自带神经网络预测其土壤水分特征参数，见表2。

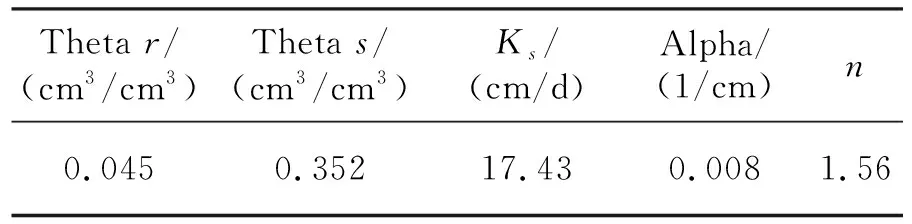
表2 土壤水分特征参数

2.2 模拟方法及数据

土壤水分运动模拟区域如图1所示。

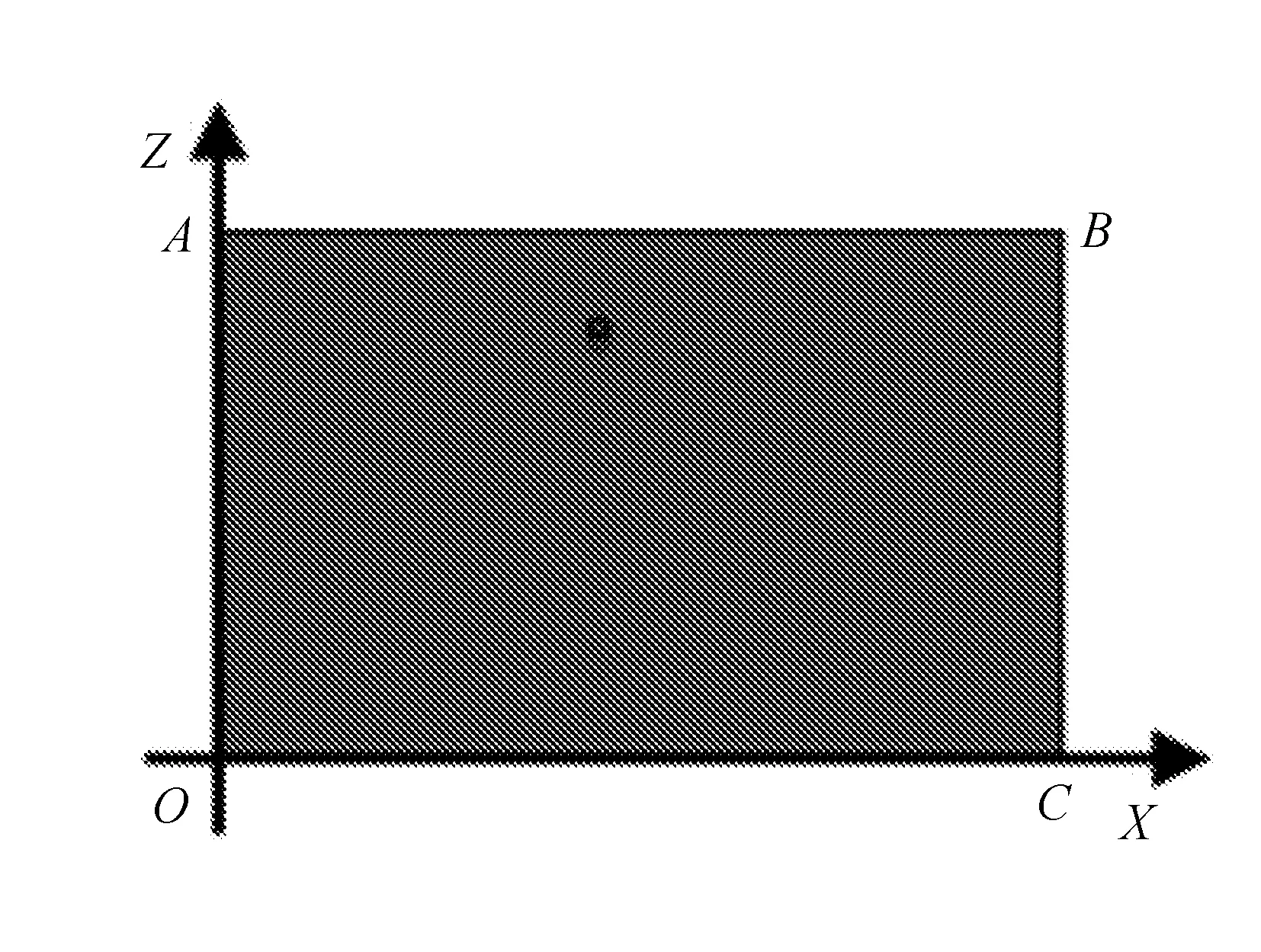
图1 土壤水分运动模拟区域

根据黄瓜根系生长范围，确定OC为100 cm，OA为80 cm。由于模拟滴灌过程模型上边界为变流量边界，边界AO，BC为试验土箱壁无水流交换，为不透水边界，边界CO为试验土箱底面已均匀打孔，可视为自由排水边界。图中点代表观测点。根据黄瓜的根系分布，确定位置在距离AB分别为10 cm深处。

数值模拟时间信息设置为12 h，初始时间步长为0.02 h，最小时间步长为0.01 h，最大时间步长为1 h。时间步长采用等间隔划分，间隔30 min。文中结合模拟试验方法，主要考虑土壤含水量变量来调节浇灌量，使土壤含水量达到黄瓜各阶段生长的最适生长环境。在以后的每次模拟试验中只需根据土壤含水量信息修改模型土壤初始含水量和变流量边界的数值,使土壤质量含水量达到黄瓜所需的最适含水量最大值31.5%(相对含水量为90%)，这样就得到了29组模拟数据。部分模型仿真数据见表3。

3 模糊控制

模糊控制理论(Fuzzy Control Theory)是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一种智能控制方法[8-9]。文中选用控制器的输入为土壤含水量(Soil Moisture Content)，输出为浇灌水量(Irrigation Water)。

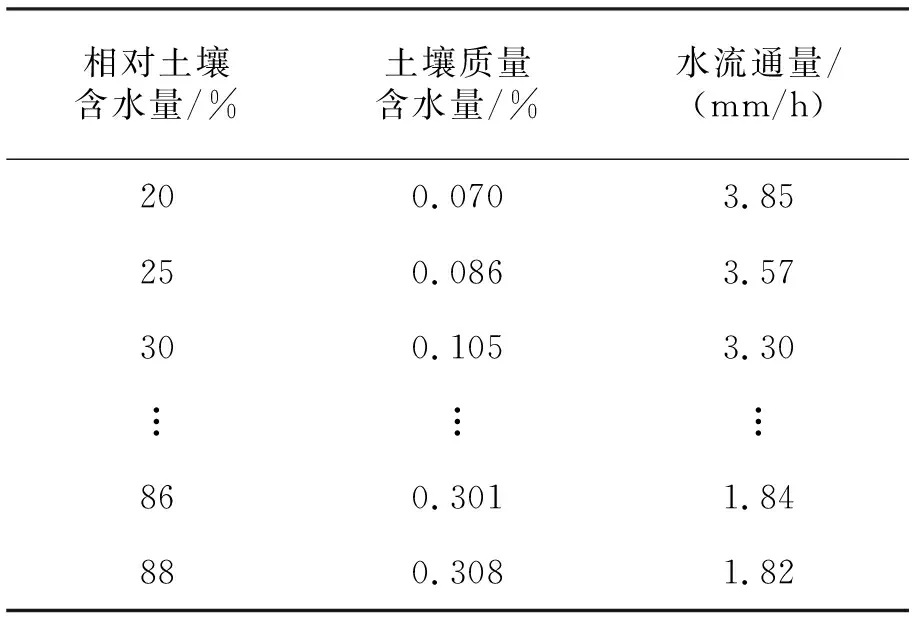
表3 部分模型仿真数据

模糊控制基本原理如图2所示。

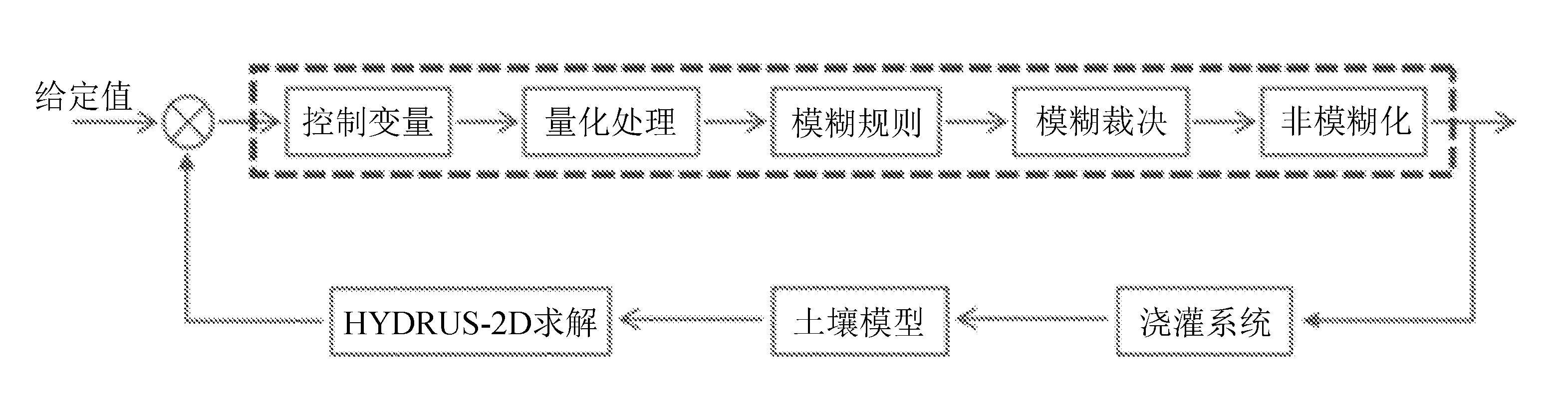
图2 模糊控制器设计的原理图

图中虚线部分为模糊控制器的核心部分。模糊控制规律由LabVIEW模糊控制器实现，经过HYDRUS-2D求解获得土壤含水量，将土壤含水量的精确量进行模糊化变成模糊量,并用相应的模糊语言表示，再根据推理的合成规则进行模糊决策，得到的模糊控制量传送给浇灌系统，对土壤模型进一步控制，通过这样的循环，实现了对土壤模型的模糊浇灌过程。

3.1 模糊化(Fuzzification)

将土壤含水量作为观测量，控制量u为浇灌水量。将土壤含水量θm和控制量u的精确值变为模糊量并分为五级：

θm= {干、稍润、润、潮、湿}=

{NB，NS，ZO，PS，PB}

u= {很少，少，中，多，很多}=

{NO，S，M，L，MX}

根据模型仿真数据，调整模型输入、输出隶属度函数。在[0,25]和[85,100]采用梯形隶属度函数，在[25,85]均采用三角形隶属函数实现土壤含水量的模糊化，给出输入土壤含水量变量隶属度函数如图3所示。

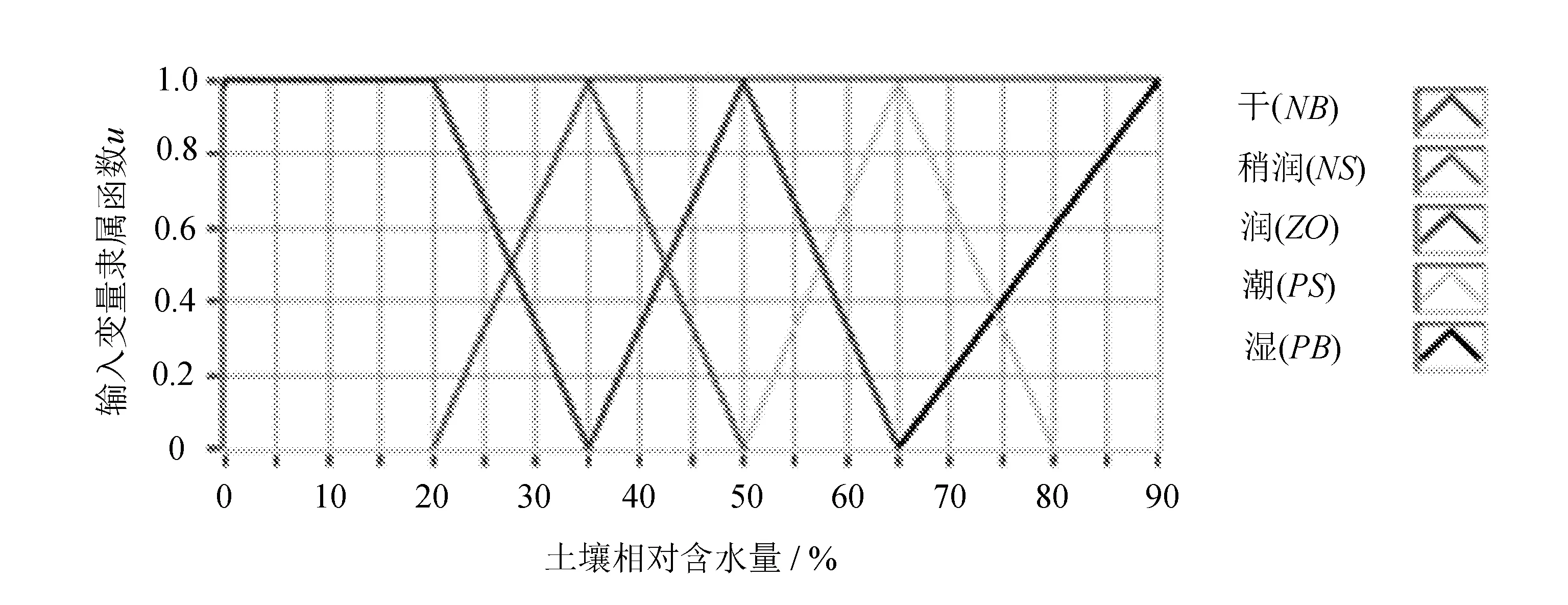
图3 土壤含水量隶属度函数

由HYDRUS-2D软件按上述条件模拟，发现当浇灌量为3.93 mm/h时，土壤含水量已达到黄瓜所需土壤含水量的最大值。由于土壤水分入渗的情况存在，即使土壤含水量很接近0.315，要使其达到0.315，最小的浇灌量也需为1.8 mm/h。所以确定浇灌水量u取值范围为[1,4]，隶属度函数如图4所示。

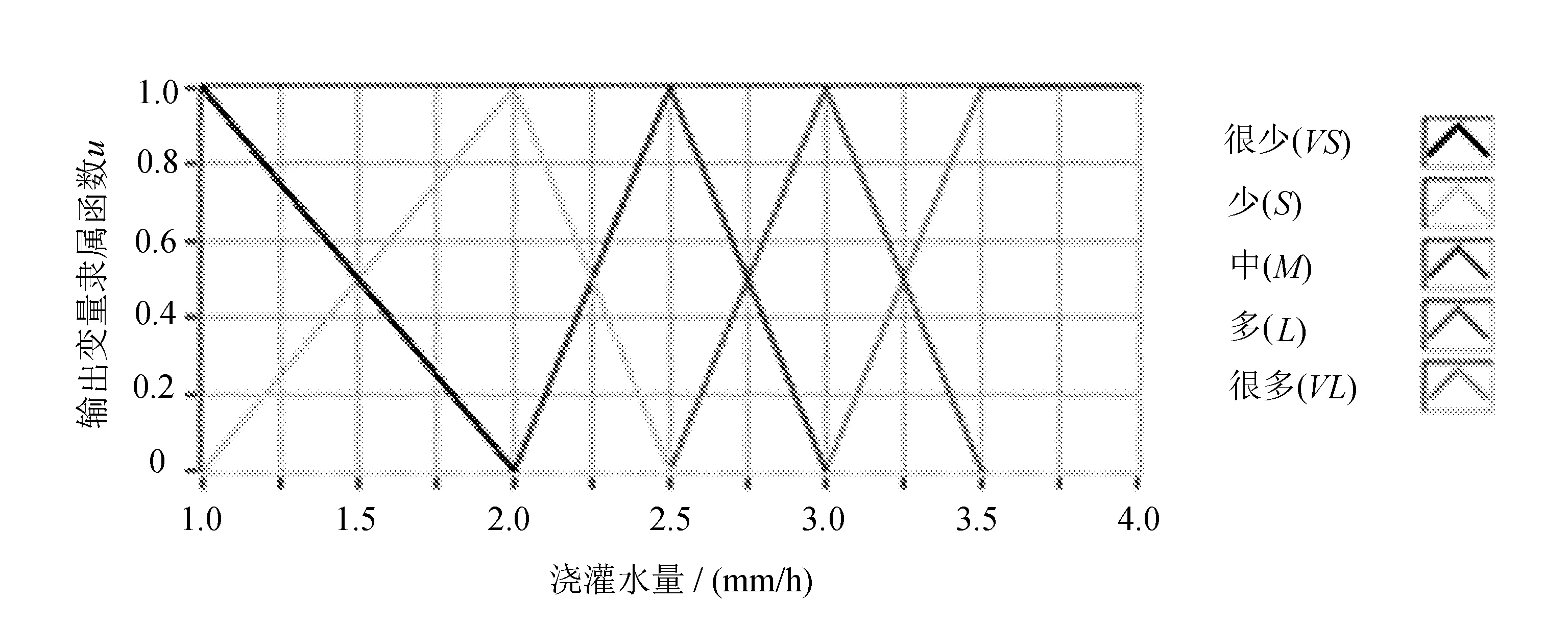
图4 浇灌水量隶属度函数

3.2 模糊裁决和非模糊化处理

设计模糊控制规则时，考虑到控制规则的完备性、交叉性和一致性。在LabVIEW建立如下专家规则：

1)IF‘土壤含水量’ IS ‘干(NB)’THEN ‘浇灌水量’ IS ‘很多(VX)’;

2)IF‘土壤含水量’ IS ‘稍润(NS)’THEN ‘浇灌水量’ IS ‘多(L)’;

3)IF‘土壤含水量’ IS ‘润(ZO)’THEN ‘浇灌水量’ IS ‘中(M)’;

4)IF‘土壤含水量’ IS ‘潮(PS)’THEN ‘浇灌水量’ IS ‘少(S)’;

5)IF‘土壤含水量’ IS ‘湿(PB)’THEN ‘浇灌水量’ IS ‘很少(VS)’。

根据上述模糊隶属度函数和模糊控制规则，给出模糊控制器输入、输出对应关系如图5所示。

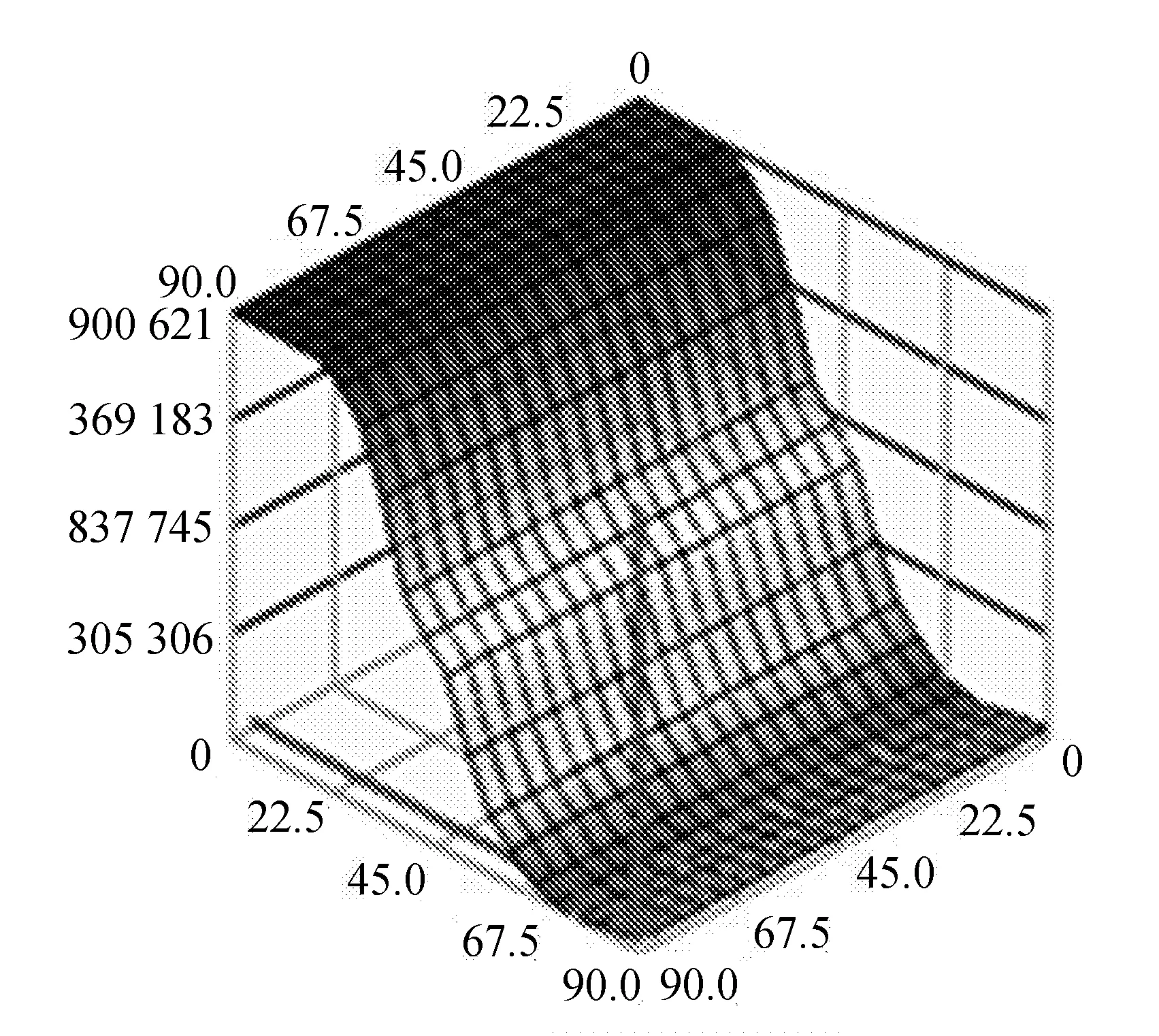
图5 模糊控制器输入、输出关系

非模糊化处理方法中，面积中心法(CoA)适用于模糊决策，均值法适用于模糊识别[10]。文中是根据土壤含水量进行模糊决策的浇灌系统，所以采用面积中心法进行非模糊化处理。

4 结果分析

当初始含水量为0.150时，不同水流通量，土壤含水量取得最大值所需要的时间如图6所示。

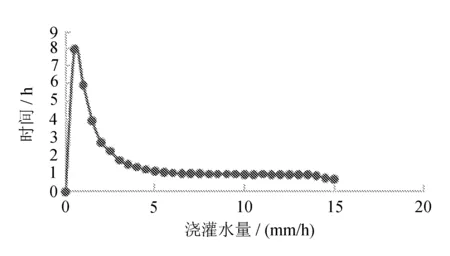
图6 浇灌水量和达到最大含水量所需时间

当水流通量为0 mm/h时，最大值也在0时刻出现；当水流通量上升为0.5 mm/h，最大值出现时间大概需要8 h左右，之后随着水流通量的不断增大，最大值出现时间不断减少。当水流通量达到饱和15 mm/h，土壤含水量达到饱和，最大值出现时间在0.71 h。由此可以看出,用实验方法得到数据所需时间非常大，而使用HYDRUS-2D模拟一次，并给出结果只需不到2 min，即使复杂的建模求解也不过数分钟。所以根据当前建模求解，效率提升至少为21.3倍。

模糊输出和HYDRUS-2D求解比较见表4。

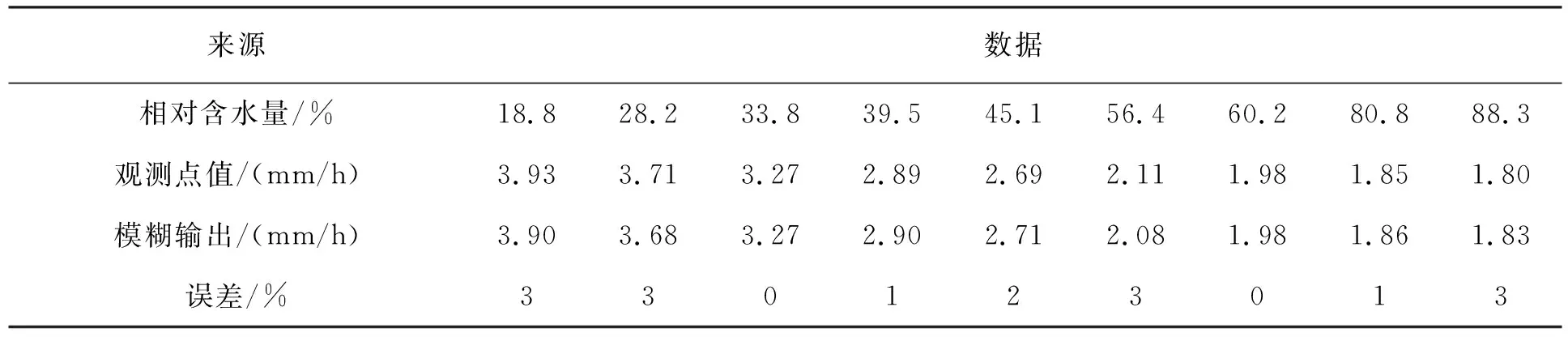
表4 模糊输出和HYDRUS-2D求解比较

由表4可知，随机选取10组模拟数据进行调控，根据初始相对水含量，使用HYDRUS-2D建模求解，当土壤含水量达到0.315时，所需要的灌溉量和模糊控制输出的灌溉量比较,结果可以看出，模糊控制输出量的值和模拟值基本一致。当相对含水量较小时，观测点值均大于模糊输出，随着时间的推移，模糊输出逐渐增大，但总体来看数据误差控制在3%以内，模型合理。

5 结 语

1)通过使用HYDRUS-2D模拟可以看出，土壤含水量达到饱和实际所需时间最少为0.71 h，而HYDRUS-2D建模求解不到2 min，效率提升至少为21.3倍。

2)利用HYDRUS-2D对所建模型进行求解，得到模拟数据来调整模糊控制隶属度函数，并随机使用10组模拟数据验证模糊控制系统输出结果。通过土壤剖面含水率随时间变化的模拟值与模糊控制输出值的对比验证，误差在3%以内，结果合理。

参考文献：

[1] 冀荣华,王婷婷,祁力钧,等.基于HYDRUS-2D的负压灌溉土壤水分入渗数值模拟[J].农业机械学报,2015,46(4):113-119.

[2] 莫彦,李光永,蔡明坤,等.基于HYDRUS-2D模型的玉米高出苗率地下滴灌开沟播种参数优选[J].农业工程学报,2017,33(17):105-112.

[3] Benye Xi, Mark Bloomberg, Michael S Watt, et al. Modeling growth response to soil water availability simulated by HYDRUS for a mature triploid Populus tomentosa plantation located on the North China Plain[J]. Agricultural Water Management,2016,176:243-254.

[4] 郭晓刚,夏颖.模糊控制在温室控制系统中的应用[J].长春工业大学学报:自然科学版,2013,34(1):50-54.

[5] 禤培录.黄瓜种植技术及病虫害防治研究[J].农技服务,2017,34(6):32，23.

[6] 周广林,王全九，李云,等.Hydrus-3D模型模拟田间点源入渗与水分再分布准确性评价[J].干旱地区农业研究,2015,33(2):113-121，129.

[7] 王维娟,牛文全，孙艳琦,等.滴头间距对双点源交汇入渗影响的模拟研究[J].西北农林科技大学学报:自然科学版,2010,38(4):219-225，234.

[8] 张德江.智能控制技术现状与展望[J].长春工业大学学报:自然科学版,2002,23(S1):58-61.

[9] 张淑霞,马跃，白羽,等.基于模糊控制的旋转型双支点倒立摆系统[J].长春工业大学学报:自然科学版,2007,28(1):109-113.

[10] 裘正军,童晓星，沈杰辉，等.基于模糊控制与虚拟仪器的灌溉决策系统研究[J].农业工程学报,2007(8):165-169.