SIFT算法在VR场景拼接中的应用

汤 强

(安徽新华学院 信息工程学院， 安徽 合肥 230088)

0 引 言

近年来，虚拟现实(VR)技术发展的风生水起，各大软硬件生产制作商都踏入这个领域，看好VR的未来。虚拟现实强调用户的体验感，利用计算机相关技术构造出一个虚拟场景，而当使用者进入到这个虚拟场景后，能否达到置身其中的真实感觉，很大一部分取决于场景搭建的是否有足够的真实感。现阶段对于场景的搭建主要有两种方法，一种是利用软件来构造一个现实中完全不存在的场景，比如用Unity3D搭建一个宇宙飞船内部的场景;另一种是利用高清相机进行现实采集照片，然后拼接成一个完整的场景，比如谷歌地图里的街景。文中讨论的就是第二种场景的搭建，利用SIFT算法对照片进行拼接来构成场景，但为了提高拼接的实时性和效果，对尺度空间结构进行了改进。

1 图像拼接技术流程及算法评价

1.1 图像拼接技术算法及流程

目前比较主流的图像拼接技术是基于特征点的匹配，该方法相比较其他图像匹配方法具有以下优点：

1)计算量小。利用特征点来进行图像匹配的技术就是在特征空间中通过计算找到两幅图像的特征点并进行匹配，然后得出对应的变换模型[1]，因此计算速度很快，计算量小。

2)鲁棒性好。特征点匹配是利用特征点在特征空间上对图像进行匹配的技术[2]，所以避免了噪声对匹配效果的影响具有更好的鲁棒性。

3)对几何的形变不敏感。基于特征点的图像匹配技术因为是在特征空间进行点的匹配，所以即使当图像发生几何形变时，对图像拼接的影响也会很小。

一个完整的场景拼接步骤是首先利用高清相机拍摄出待拼接的场景图片，然后对这些图片进行预处理，提取特征点，再进行匹配，最后进行融合和相应的亮度处理，然后将拼接好的完整图像输出。

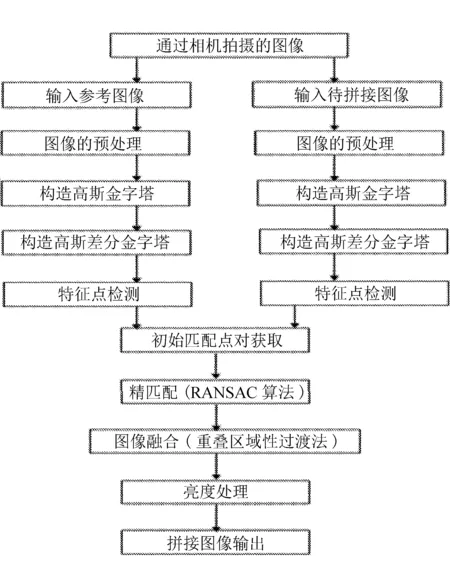
图1 图像拼接流程

1.2 图像拼接算法评价标准

图像拼接算法将直接影响到图像拼接最后呈现出的效果的完整性、真实性，是否有拼接痕迹。对于不同的算法，人们在评判其好坏时，一般从两个方面去评价，一是精确度，二是速度。所谓精确度，指的是该算法可以对两幅甚至更多幅图像进行精准的拼接，所得到的图像拼接痕迹非常小。而速度是指利用该算法拼接图像所耗费的时间的长短。但这两个评价要求其实又是自相矛盾的，因为如果希望对图像进行精准拼接，那么就必然要求提高特征的独特性，因此需要对特征进行更复杂的描述，同时也需要引进更多的特征点,从而进一步提高拼接质量。这样处理的代价就是会极大地提高算法的复杂性，并且会带来运行时间过长的弊端，特别是对于实时系统来说，这将会成为更加严重的问题。因为对于算法优劣的评价并不能一概而论，而是要根据算法应用的场景，不同的场景下对算法的需求也会有不同的标准。但是在速度和精确度之间找到平衡，仍然是大多数算法追求的目标。

2 基于尺度空间的SIFT配准

2.1 图像配准技术

在图像拼接技术中，图像配准是一个基础工作，但同时也是拼接流程中的关键性工作，它直接影响到拼接之后图像所呈现出来的效果。而利用特征点进行图像配准是近几年图像拼接领域里的一个热门技术，该配准算法首先是对待拼接图像进行特征点检测，然后对检测到的特征点进行描述，再将描述一致的特征点进行匹配，最后再通过算法对误匹配的特征点进行消除。在这几个步骤中，关键的一步是特征点检测，它将直接影响后续的特征点匹配和误匹配率，例如大家熟悉的Harris角点检测算法[3]。但该方法有一个弊端，就是当待检测的图像如果发生了图像尺度变化，并且变化幅度比较大，那么该算法在检测过程中会出现很大的误差，忽略很多特征点的检测，因此在图像特征不变性这一点上，很难得到保证。针对该问题，David Lowe于1999年提出了SIFT算子，并在2004年正式提出了SIFT特征[4]，该特征是图像在尺度空间时的局部特征，当图像发生平移、旋转或者缩放这些变化时，该特征在尺度空间上却仍然可以保持不变，并且该特征对视角变换和噪声也有一定程度的稳定性[5]，所以是一种匹配能力较强的算法。

2.2 SIFT算法性能分析

SIFT算法性能分析实验图如图2所示。

图2 SIFT算法性能分析实验图

以图2(300*400)为例，进行了SIFT算法检测特征子，共实验20次，并对实验过程中的关键步骤进行计时，然后进行平均计算，结果见表1。

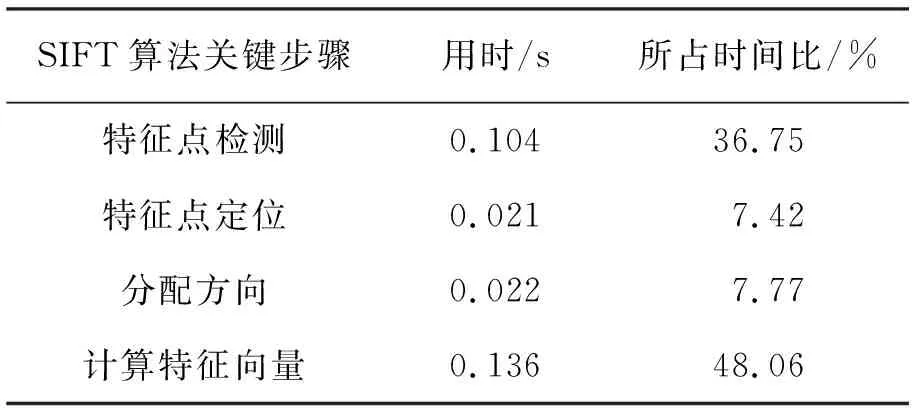
表1 SIFT匹配算法关键步骤用时表

通过表1可以发现，在SIFT匹配算法关键步骤中，用时最多的是特征点检测和计算特征向量，分别占到了36.75%和48.06%。

这是因为在进行特征点检测时，SIFT匹配算法会对尺度空间和高斯差分尺度空间进行计算，很明显，当高斯金字塔阶数和层数增多，SIFT算法的计算量就会增大[6]，同时，计算的像素点的数量也会增多，那么就会使算法的计算速度进一步降低。

3 尺度空间构造结构的改进

利用SIFT算法构造高斯金字塔时，一般选择的是四阶五层，在构造过程中要注意，通常会将原始图像进行放大，然后作为第一阶的第一层，这样做的目的是为了能够得到更多的特征点，并假设该层的空间尺度因子为σ[7]。同时,假设同一阶中相邻两层的尺度空间比例因子为k，那么第二层的尺度空间因子为kσ，第三层为k2σ，第四层为k3σ，第五层为k4σ。当继续构建高斯金字塔第二阶时，第一层选择的是第一阶的第三层，所以第二阶第一层尺度空间因子为k2σ，第二层为k3σ，第三层为k4σ，第四层为k5σ，第五层为k6σ。构建第三阶和第四阶也按照同样的方法。具体如图3所示。

位于宜兴的木构农房绿色改良技术集成与示范项目，隶属于郑州大学主持的“十二五”国家科技支撑计划课题“传统农房建造技术改良与应用”（2015BAL03B03）。项目运用现代木结构技术，改善传统木构民居在结构安全、房屋节能、居住舒适度、建造方式等问题。笔者在郑州大学研究生在读期间有幸参与了项目设计建造的全过程。

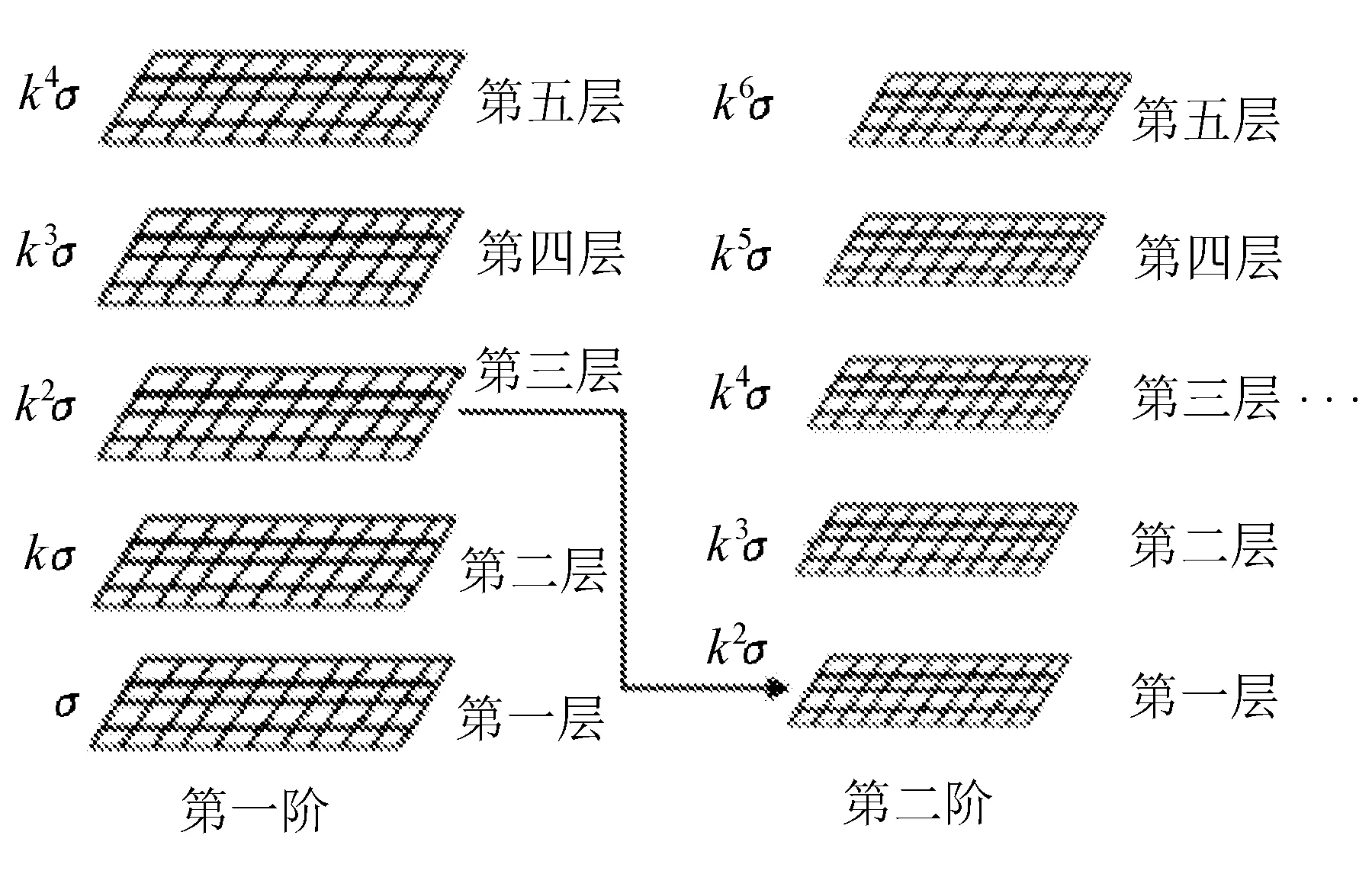
图3 高斯金字塔构造图

既然四阶五层的高斯金字塔导致了计算量增多和计算速度下降，那么可以尝试减少阶数和层数，例如构建一个三阶四层的高斯金字塔来进行验证。

当高斯金字塔的阶数和层数都减少后，先通过下面一个简单的分析，看看对算法的计算量和计算速度有什么影响。

假设m为高斯金字塔的阶数，n为高斯金字塔的层数，Ci,j为第i阶j层的特征点数目，那么这样一个高斯金字塔的特征点总的数量为[8]。

通过上述公式容易知道，当高斯金字塔的阶数和层数减少后，整个高斯金字塔的特征点的总数必然会减少，而特征点数量的减少，虽然会减少算法的计算量，提高计算速度，但必然会影响图片拼接的质量和效果。以图2作为实验用图，通过实验得出特征点分布，当取三阶四层时，得到了81个特征点，而取四阶五层时，可以得到102个特征点。因此，当高斯金字塔由四阶五层减少到三阶四层时，特征点数量减少了，那么两幅图像的匹配点的对数也会相应减少，在一定程度上影响投影变换矩阵的精确计算和图片的拼接效果。为了解决这个问题，文中将采用RANSAC算法对匹配点进行提纯的方法，降低因为高斯金字塔阶数和层数的减少带来的精度的缺失，同时提高拼接后图片所呈现出的效果和质量。

3.1 改进的实验效果和分析

本次实验选择两幅图像作为拼接对象，如图4所示。

(a) 待配准图 (b) 参考图

3.2 构造高斯金字塔

构造高斯金字塔一般分为两个步骤:

1)为了降低图像噪声和细节层次，通常采取高斯模糊来对图像进行处理;

2)降低原始图像的采样点，即我们常说的降采样处理。

文中将图4(288*400)构造成三阶四层的高斯金字塔，以第一阶为例，显示结果如图5所示。

图5 高斯金字塔第一阶(三阶四层)

由图5可以看出，阶数和层数越高，图像越模糊，越底层图像越清楚。这是因为在图像处理软件中，为了降低图像的噪声及细节层次，采用高斯模糊这样的处理方式。其次，我们发现在高斯金字塔的每一阶都有7幅图像，即七层，但按照理论来说，每一层一幅图像，一阶有四层，那就应该是4幅图像，但实际情况为什么是7幅？其原因在于当对图像进行极值比较检测特征点时，每一阶的首层和末层这两层的图像是无法进行极值比较的，而多出来的3幅图像其实是利用了高斯模糊在每一阶的顶层产生的，目的是为了保证尺度变化的连续性[8]，这样，每一阶的图像数量就变成了7幅，层数也就是七层。

3.3 构造高斯差分金字塔

在构造好的高斯金字塔的基础上，可以着手构造高斯差分金字塔，其实构造高斯金字塔的目的就是为了构造高斯差分金字塔。高斯差分金字塔的第一阶第一层是由高斯金字塔的第一阶第二层减去第一层得到的，每一层的差分图像都由此推导出，这些差分图像就构成了我们常见的高斯差分金字塔，因此，这就是高斯差分金字塔为什么每一阶都比高斯金字塔少一层的原因。结果如图6所示(以第一阶为例)。

图6 高斯差分金字塔第一阶(三阶四层)

3.4 特征点检测

通过对原始图像分别构造的三阶四层金字塔和四阶五层金字塔进行特征点检测和所花费时间进行对比，得到相关数据见表2。

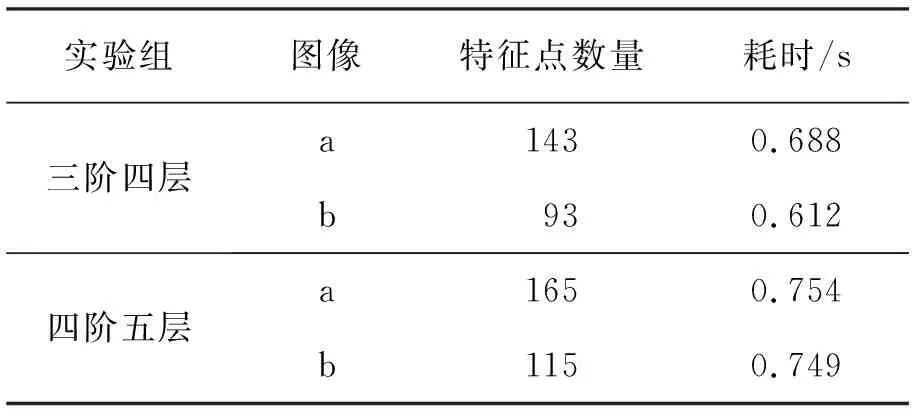
表2 两组图像特征点检测与耗时表

通过表2可以看出，当高斯金字塔由四阶五层减少为三阶四层时，特征点检测所消耗的时间减少了，因此算法的实时性得到了一定的提高。

3.5 特征点初始匹配(粗匹配)

所谓初始匹配，即粗匹配，是指利用NN法粗匹配后获得的匹配点对[6]。

当对高斯金字塔为三阶四层的图像进行粗匹配时，得到匹配的特征点对数为24对，而当高斯金字塔增加阶数和层数变成四阶五层时,对两幅图像进行粗匹配，由于特征点数目增加了，所以得到匹配的特征点对数为29对。而在之前已经介绍过了，当匹配点对数减少后，会对投影变换矩阵的精确计算带来一定的影响。因此，为了降低特征点减少带来的匹配精确度上的损失，提高图像匹配的效果，引入了RANSAC算法来对匹配后的特征点进行提纯。

3.6 匹配点提纯

在上述粗匹配所得到的匹配点对里，可能会存在着一些误匹配点对，这是因为图像背景在某些位置存在着一定的相似性。因此需要对匹配点进行提纯，所谓的提纯，就是在已经匹配的特征点里找出正确的匹配点对，去除误匹配的特征点。而提纯常用的算法就是RANSAC算法，该算法是对模型参数进行估算的一种数学方法，主要是通过计算含有异常数据的样本数据集，得出该样本数据集的数学模型参数[8]，然后根据该模型得到最终有效的样本数据的一种算法。根据该算法分别对三阶四层和四阶五层的粗匹配后包含误匹配的匹配点对进行计算，从而得到精确的匹配点对。

通过对三阶四层和四阶五层进行精匹配后得到的数据见表3。

表3 特征点匹配对数和误匹配率

通过表3可以发现，当减少了阶数和层数后，误匹配率反而降低了，这是因为图像的特征点主要集中在高斯金字塔的底层，当高斯金字塔的阶数和层数在不断提高，图像也在不断地进行着高斯模糊，因此,各阶层图像的像素值很少变化甚至是没有变化，造成了层数和阶数越高，图像的相似度就越高，而特征点检测本质是基于特征变化尽可能多的点。因而尽管可以检测到极值点，但这样的匹配点对有极大的可能成为误匹配点对。

3.7 图像融合

当高斯金字塔分别为三阶四层和四阶五层时，使用常见的重叠区线性过渡法[9]进行图像拼接，具体效果如图7和图8所示。

图7 三阶四层拼接效果图

图8 四阶五层拼接效果图

从图7和图8两幅效果图来看，高斯金字塔分别为三阶四层和四阶五层，拼接出来的效果无明显差别。拼接所耗费的时间见表4。

表4 两组图像拼接耗时对比表

通过表4可以看出，高斯金字塔由四阶五层降低为三阶四层后，拼接图像的时间降低了16.03%。

4 结 语

在图像配准阶段，针对SIFT特征点检测耗时较多的问题，提出了修改高斯金字塔的空间尺度结构，并针对改进后的高斯金字塔和传统的高斯金字塔在图像拼接过程中所消耗的时间和拼接效果的比较，证明了改进后图像拼接质量并没有降低，但拼接速度却比没改进前更加快了。但文中实验只是基于两幅图像的拼接，对于多图像拼接问题并没有分析，这也是不足之处。

参考文献：

[1] 余怀,杨文.一种无人机航拍影像快速特征提取与匹配算法[J].电子与信息学报，2016，38(3):509-516.

[2] 李玉峰,李广泽,谷绍湖,等.基于区域分块与尺度不变特征变换的图像拼接算法[J].光学精密工程，2016，24(5):1197-1205.

[3] 张斌.巡航机器人的图像拼接系统研究与实现[D].成都:西南科技大学,2015.

[4] 李秀华,刘国锐.一种改进的SIFT特征匹配算法[J].长春工业大学学报,2017,38(1):58-61.

[5] 李丹,孙海涛,王海莉.一种改进的SIFT图像立体匹配算法[J].西南交通大学学报,2015,50(3):490-495.

[6] 秦佳,杨建峰,薛彬,等.基于向量相似度匹配准则的图像配准与拼接[J].微电子学与计算机,2013,30(6):22-25.

[7] 赵宏宋,潘地林.基于SIFT和函数强制改正算法的图像拼接研究[J].电脑知识与技术,2014,10(14):3372-3375.

[8] 欧阳宁,翟紫伶,首照宇,等.基于图切割的多频带融合图像拼接[J].微电子学与计算机,2013,30(7):107-110.

[9] 赵毅力,武仲科，张雁,等.基于图结构的全景图自动识别与拼接技术[J].计算机工程与技术,2013,34(6):2067-2070.