基于熵原理和狭义相对论的空间量子化研究

钱凤仪

(吉林大学 研究生院， 吉林 长春 130012)

0 引 言

在研究黑体辐射吸收规律时，普朗克在1900年提出了能量量子化概念，其主要内容是：黑体由不同频率作简谐振动的振子组成，其中电磁波的吸收和发射不是连续的，而是以一种最小的能量单位[1]

ε=hν

(1)

为最基本单位而变化着的。这样以不连续增加的一份能量ε称为能量子。其中ν是辐射电磁波的频率，h即普朗克常量。也就是说，振子的每一个可能的状态以及各个可能状态之间的能量差只能是hν的整数倍。

受普朗克能量子假设的启发，爱因斯坦于1905年提出，在空间传播的光也是不连续的，也是一份一份的，每一份叫一个光量子，简称光子。光子的能量E同光的频率ν成正比。这个假说后来就叫爱因斯坦光量子假说。光量子假说认为每一个光子的能量只决定于光子的频率，例如蓝光的频率比红光高，所以蓝光光子的能量比红光光子的能量大。而同样颜色的光，强弱的不同则反映了单位时间内射到单位面积的光子数的多少。

近代物理学最主要理论是量子理论和相对论。在狭义相对论中，光子能量方程为

E=hν

(2)

对光子而言，光沿着x方向传播时其速度C的表达式为

(3)

按照狭义相对论，时间间隔表达式为[2]：

(4)

式中： Δτ——原时，是平坦空间中的我们观测者所处空间的时间间隔；

Δt′——物体以速度V相对我们运动时，在我们“看来”它在我们所处的坐标系形成的时间间隔。

由式(4)可知，当

V→C

(5)

或对光子而言

V=C

(6)

时，则由式(4)可知

Δt′→∞

(7)

也就是说，当光子以光速运动时，它的时间间隔在我们看来是无限漫长的，或者说时间过程无限慢,也就是时间消失了。这在理论上表明，光子无论以什么频率变化，但按照狭义相对论及频率与时间间隔关系式

(8)

可知，当光子以光速C相对我们运动时，其时间间隔变为式(4)和式(7)中的Δt′，因此光子的变化频率为

(9)

式(9)表明，按照狭义相对论，光子以光速运动时，光的频率变化是不能显现的，这与式(2)中爱因斯坦所假设的光子能量方程是不一致的。由此看来，狭义相对论与光量子方程之间在光速这个边界上存在矛盾。按照狭义相对论，光子不应该有频率，按照光量子方程，只有假设光子有频率，才能与对应的物理实验相符合。这就需要在光速边界问题上修改狭义相对论对关于时间间隔问题上的不正确的描述或不能充分描述客观现象的事实。

1 经典谐振子能量方程与量子化问题

在低速情况下，一个质量为m的物体，以角频率ω作周期运动时，对应的谐振子势能为[3]

(10)

式中:k——胡克常数。

令

(11)

可得对应的薛定谔方程为

(12)

由式(12)可求得厄密多项式能量量子化解[3]为

(13)

由式(13)可知,谐振子的能量级是均匀分布的，量子的能量最小值为

ħω0

(14)

由式(13)和式(14)可知，量子的最小值不是0，而是E0。量子之间的能量间隔或能级也是不连续的，而是

Es=ħω0

(15)

由式(14)可知,对于一个质量不为0的谐振子而言，它的能量最小值不能是0。推而广之，光子的能量同样不能降低为0。这就是为什么普朗克将辐射能量假设为式(1)和爱因斯坦将光子的方程假设为式(2)的原因。

在经典力学中，三维空间中线性谐振子的运动是简谐运动。其势能表达式为：

(16)

其中

x=Asin(ωt+φ)

(17)

式中：φ——相位初始值；

A——振幅；

ω——角频率。

由式(16)和式(17)可将能量子势能最大值写成

(18)

以谐振子的周期ΔT为时间间隔，则有

(19)

换而言之，在非量子情况下，式(18)给出的能量微分也就是能量最小值

dEmax=mA2ωdω

(20)

由式(19)将式(20)表示为关于时间的微分，就是

(21)

或

(22)

由式(1)和式(2)可知，三维空间中的物理量dt2在二维空间中收缩为2dt；或者二维空间中的时间间隔这个物理量2dt，在三维空间中则通过积分扩张为dt2。因此，谐振子的能量表达式在三维空间中是式(22)所表达的与时间间隔的平方dt2成反比，而一旦谐振子处在以光速运动的二维空间，则收缩为如式(2)所表达的与时间间隔成反比。这种变化的原因是三维空间和二维空间里空间能量子的熵S是不同的。而且理论上，二维空间中的熵是三维空间中熵的微分。

2 借助熵原理对光量子或空间能量子的量子化

如果用熵S代表空间的混乱度，由玻尔兹曼公式可知

S=klnΩ

(23)

式中:k——玻尔兹曼常数;

Ω——宏观粒子配容数或分配数。

由克劳修斯熵公式

(24)

其中

Q=dA+dE

(25)

dA——系统作功，dA=pdV；

dE——内能的增加，dE=Cv,mdT。

由式(24)可知，在背景温度不变的情况下，尤其在宇宙背景温度相对不变的条件下，熵的变化是与能量成正比的。所以，若粒子的运动速度为V，则熵S与粒子的能量关系为

(26)

式(26)表明，如果系统的粒子都处在静止状态，则系统内的混乱度等于0。当粒子系统以速度V与观测者做相对运动时，由式(4)、式(7)、式(26)可知，当V→C

(27)

式(27)表明，在光速的情况下，光子在所处的空间之内，其空间能量子混乱度依然不为0。因此，光子即使在光速条件下，按照狭义相对论，它就不应当有运动和变化发生，但按照量子的观点，光子还会在二维空间内发生变化的。其变化的能量表达式如同式(2)。也就是说，当光子以V=C运动时，由于空间还是有熵效应的,或者说还是有时间效应的，只不过此时的光子处在二维空间内，时间间隔也是二维空间下的时间，空间的能量子熵也是二维空间之下的熵。

借助式(26)和式(27)，将式(4)改写为

(28)

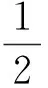
在一维空间内，粒子的运动只能在一维线空间之中震动，且一维空间内空间的熵或能量子混乱度S1x是二维空间内空间的熵或混乱度S1yz微分，即

S1x=(S2yz)′

(29A)

同理,二维空间内空间的熵或能量子混乱度S2yz是三维空间内空间的熵或混乱度S3yz微分，即

S2yz=(S3xyz)′

(29B)

在二维空间内，粒子的运动只能在二维面空间内震动，此时多粒子或能量子是能够形成混乱度或进行位置交换的，所以由式(24)可知，若粒子或空间能量子的谐振能量为E2yz，则对应的熵为

S2yz=k2yzE2yz

(30)

式中:k2yz——比例常数。

对三维空间中的谐振子而言，若谐振子角频率为ω，则有

V=Aω

(31)

式中:A——振幅或圆周运动的半径。

由式(31)和式(16)或式(26)可知,三维空间内的能量子熵与能量关系为

(32)

借助式(31)可得：

(33)

考虑到空间能量子可以看做是连续的，则三维空间中的熵就是对二维空间中熵的积分，也就是二维空间中的熵是对三维空间的积分，所以有

S2yz=(S3xyz)′=ksmA2ω

(34)

令常数

(35)

则有

S2yz=hν

(36)

式(36)就是用熵所代表的式(2)的能量方程，也就是通过空间的熵效应得出的爱因斯坦关于光子能量方程。上式推导也说明，正是因为空间是量子化的，所以观测者所在的坐标系中空间的熵与运动物体所在空间的熵是不一致的，才导致了时间上的狭义相对论效应，也就是说，相对观测者而言，处在运动坐标系中的空间所对应的空间中的熵，在观测者看来，空间的能量子的熵发生了变化，所以导致了运动坐标系中的时间间隔被拉长了。

由于一维空间中的熵是对二维空间中熵的微分，所以一维空间的熵为常数。而二维空间能量子的最小能量值，就是其在一维空间中的能量值。因此光子的能量最小值Emin由式(33)～式(36)和式(2)，也就是通过对式(36)两侧直接求导可知

Emin=h

(37)

由质能关系式可知，光子的最小质量为

(38)

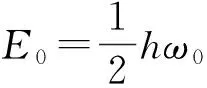
将式(33)改写为

(39)

令

ksT=2ksmA2π2

(40)

则有

(41)

由式(41)可知，空间中的时间间隔作为往复有序的周期现象，与空间中能量子的混乱度相互对应。可以说空间的熵是空间中时间间隔取平方的倒数，或者说，空间中的时间间隔作为一个量子周期现象，它是空间熵效应(空间混乱度)的倒数开方。

以上讨论表明，光子的能量变化也是不连续的。由于光子静止质量在狭义相对论理论上只能为0，所以暗物质只是按照狭义相对论而言，是不可见的。但空间量子化之后，光子的静止质量不为0，所以理论上我们会遇到暗物质现象。

如果时间间隔Δt→∞，由式(41)可知，S→0。由此可知，狭义相对论中假设“光速在任意一个惯性系中是不变的”，其物理机制是由光速条件下空间的熵为0。熵作为标量，在惯性系变化中始终为0，因此,光速在任意一个惯性系变换过程中，物理上就必然是始终保持不变的。

应该注意的是，式(37)中的h量纲与式(2)中的h量纲是不同的，但数值是相同的。我们用hp代替式(37)中的h。则式(37)变为

Emin=hp

(42)

则式(13)变为

(43)

由此可知，光子的能级间隔是2hp。换而言之，光子的频率变化也不是连续的，而是有能级间隔的。只不过这个能级间隔非常小，是普朗克常量的2倍。

3 光子静止质量或空间能量子不为0的重要意义

按照经典理论，谐振子比如电子的最低能量可以是0，但量子理论给出的结论是，能量是不连续的，是有能级的，而且量子的最小能量也不是0。文中以此论证了光子按照狭义相对论，其静止质量必须为0，但通过熵原理，从理论上不仅能推导出爱因斯坦的光量子方程，还论证了光子的静止质量不为0，而且论证了以光速运动的空间其时间间隔也不是无限长而变得没有时间间隔。文中在理论上论证光子的静止质量或最小质量不为0，所以从理论上能够推断出暗物质是空间的冻结，或大质量星体(星系)对空间能量子的冻结。空间能量子相当于光子的静止质量。空间能量子的速度只有与光速相同，光子才能以光速运动。如果空间能量子的速度小于光速，就是出现超光速的问题，这在狭义相对论中是不允许的。按照狭义相对论，光子的静止质量或空间能量子的质量是0，光子的被加速到光速是不可能的。按照狭义相对论，光子的静止质量或空间能量子的能量必须是0。但从理论上，能量值为0的空间能量子或光子变为暗物质是不可思议的，因为这在逻辑上是可以无中生有的问题，是不可能发生的问题。而且光子的静止质量或空间能量子的质量是0，引力场是无法形成的[4]。因此，只有光子的静止质量或空间能量子的质量不为0，光子静止质量或空间能量子在引力场的作用下才能因为凝聚而形成暗物质。事实上，只有空间的能量子不为0，空间才能形成引力场。若传播以光速传播引力的引力子，其静止质量为0，一方面理论物理又得回到以太学说中去；另一方面就是式(2)中，当光子能量转化为电子的动能时，光子是否真的变为静止了。因此光子能量量子化，具有非常重要的理论价值。

4 结 语

论述了狭义相对论中的时间相对论效应，其实质是空间能量子的熵效应所导致的。对狭义相对论中光子和爱因斯坦在光量子方程中给出的光子表达式进行了量子化，在此基础上，论证了光子的静止质量不为0，从而为“暗物质是空间能量子在引力的作用下导致的冻结”这一论断提供了可靠的理论依据，因而对从事暗物质的理论研究者以及具体实验的观测者具有重要的理论参考价值。

参考文献：

[1] 张三慧.大学物理学[M].北京.清华大学出版社,2010.

[2] 吴大猷.相对论[M].北京:科学出版社,1983.

[3] 曾谨言.量子力学[M].北京:科学出版社,1984.

[4] 钱凤仪.相互作用原理[M].长春:吉林科技出版社,1999.