基于box-cox变换回归模型的中国婚恋状况分析

王纯杰， 张诗羽

(长春工业大学 数学与统计学院， 吉林 长春 130012)

0 引 言

婚姻是人类社会生活的重要体现，对社会的结构影响重大[1]。20世纪70年代末以来，中国离婚率持续增加，引起了国内外学者的关注。建模过程中选择9个指标[2-4]，考察这些因素对婚姻状况的影响，通过运用回归分析模型探究变量粗离婚率与各相关指标的关系。文中建立了全因素模型、逐步回归模型、岭回归模型[5]，并结合数学模型实际意义给出结论与建议。

1 源数据与指标

文中研究数据为1996-2014年的19条纵向年度数据，所研究的地区为全国范围。研究的因变量选定为粗离婚率。解释变量的选择从三个角度入手：一是经济水平(居民消费水平、房地产住宅投资)；二是受教育水平(年度普通本专科招生数、研究生招生数)；三是社会参数水平(第三产业GDP贡献率、第三产业增加值、移动电话普及率、男性人口、女性人口)。变量声明和源数据分别见表1和表2。

表1 变量声明

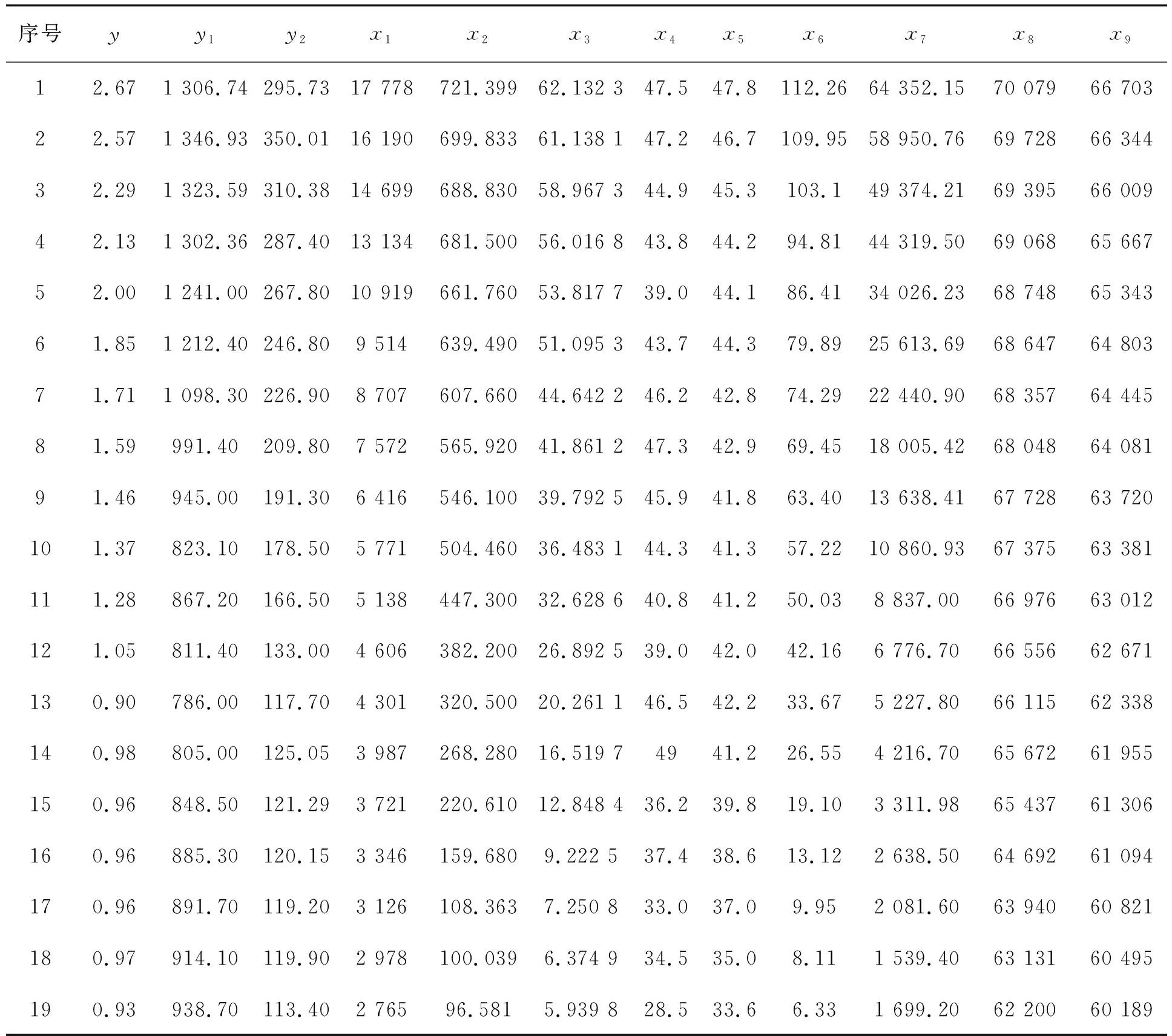
表2 源数据

2 多元回归模型原理

设随机变量y与p个解释变量x1,x2,…,xp的线性回归模型[6-7]为：

y=β0+β1x1+β2x2+…+βpxp+ε

(1)

式中：β0,β1,β2,…,βp——p+1个未知参数；

β0——回归常数；

β1,β2,…,βp——回归系数；

y——被解释变量；

x1,x2,…,xp——p个可以精确测量并控制的一般变量，称为解释变量；

ε——随机误差，对随机误差项假定

(2)

对一个实际问题，如果获得n组观测数据(xi1,xi2,…xip,yi)(i=1,2,…,n),则线性回归模型可表示为

(3)

上式的矩阵形式为

y=Xβ+ε

(4)

其中

(5)

X是一个n×(p+1)阶矩阵，称为回归设计矩阵或资料矩阵。

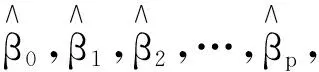
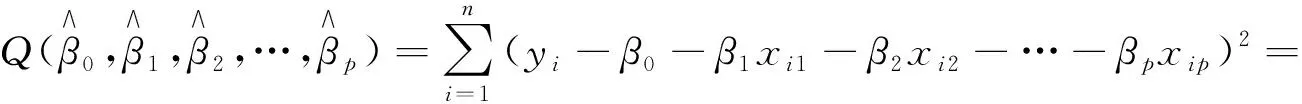
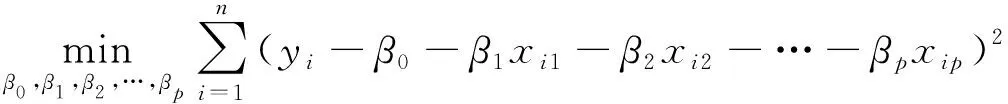
(6)

(7)

移项得

(8)

当(X′X)-1存在时，即得回归参数的最小二乘估计为

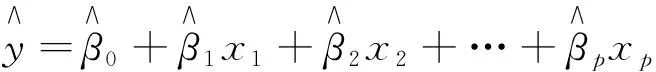
(9)

式(9)为经验回归方程。

3 模型求解

在建模之前，首先对各指标进行相关性分析。经SAS软件corr过程步得到y与9个解释变量的相关矩阵见表3。

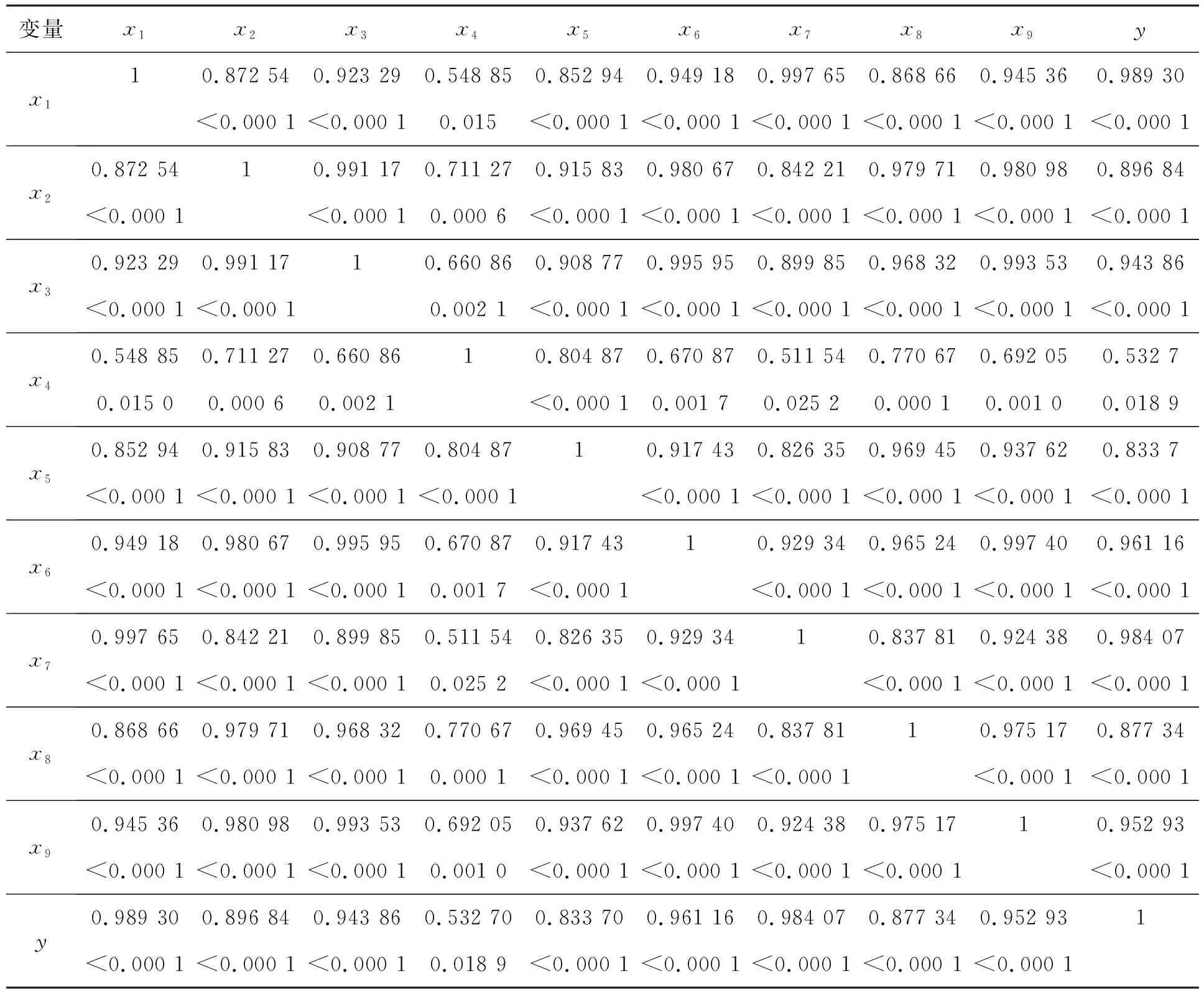
表3 全模型Pearson相关系数

可以看出,y与各解释变量的相关系数基本都属于0.8～1.0范围内。

但通过表3也可以明显看出，各解释变量之间存在高度相关性，这说明全模型存在着实际回归问题中常出现的多重共线性。显然，直接使用全模型进行回归是不合理的。

为解决多重共线性问题，文中的思路是使用逐步回归法选取最优变量集，在最优子集基础上再进行普通最小二乘回归。取显著水平aentry=0.1，aremoval=0.15情况下，SAS程序在9个解释变量中选择了3个，分别为x1，x3，x5，见表4。

表4 逐步回归模型汇总

入选变量的p值均小于0.05，通过了显著性检验。此时对最优变量集做普通最小二乘回归，并用方差膨胀因子法检验多重共线性，分别见表5和表6。

表5 选模型方差分析

表6 选模型拟合优度

此时，Pr<0.000 1,即基于逐步回归所生成的选模型显著有效，R2=0.992 1，即选模型拟合程度为99.21%。这样看来,逐步回归后基于最优子集的选模型很好地拟合了源数据。

选模型的参数估计和假设检验结果见表7。

表7 选模型参数估计及多重共线性检验

显然在选模型下的回归系数均通过了检验，即各解释变量系数均显著不为0。此时方差膨胀因子也在正常范围内，认为选模型没有出现多重共线性。由表中读出参数的估计值，可得模型：

y= 1.735 2+0.000 10x1+0.010 92x3-

0.032 81x5

(10)

由于实际问题是错综复杂的，因此在建立实际问题的回归模型时，会出现某一因素或某些因素随着解释变量观测值的变化而变化，导致随机误差项产生不同的方差，违背了方差齐性的原假设公式，也就是常说的异方差现象。模型(10)的残差直观来看较为分散且没有明显趋势，但为给出更可靠的结果，文中进行spearman相关系数检验，以判断基于逐步回归的选模型是否存在异方差性，见表8。

可见，在置信水平为0.05的情况下，选模型不存在异方差现象。但倘若模型违背了随机误差项是无关的这一条假设，就会存在自相关现象。为判断模型(10)是否存在自相关性，运用DW法检验。

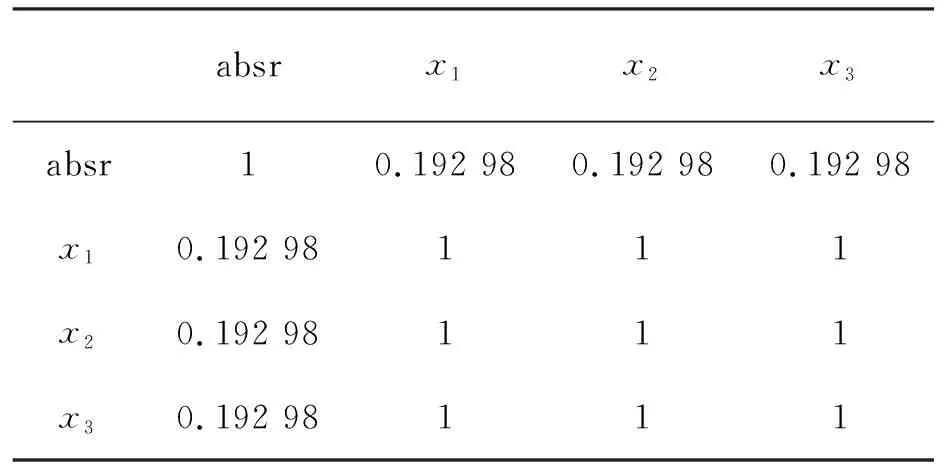
表8 选模型spearman相关系数法判断异方差

表9 选模型DW检验自相关

根据样本量n=19与解释变量数目p=4(包含常数项)，查DW分布表，得到临界值dL=0.97，dU=1.68，依照DW准则模型落入不能确定区域。

为消除这一现象，对选模型进行一步box-cox变换，见表10。

表10 box-cox变换模型拟合优度

变换后模型拟合程度为99.11%。选取lambda=1.4，对模型(10)变换。

根据box-cox变换后输出的参数估计结果，y(1.4)对x的回归方程为：

68+0.000 10x1-0.002 54x3-0.038 50x5

(11)

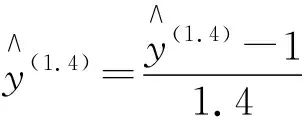
(12)

为解决模型多重共线性问题，选择从模型的数据角度考虑，采用剔除解释变量的方法来克服多重共线性的影响，最终得到模型(12)，但这始终是基于普通最小二乘估计。而近40年来，统计学家还对普通最小二乘估计提出了一些改进方法。目前，岭回归就是最有影响的一种新的估计方法，在此，文中列举岭回归建模结果以作参考。

考虑到变量的量纲问题，先将数据标准化。由于岭参数k不是唯一确定的，所以得到的岭回归估计模型是一个估计族，选定k的过程就显得至关重要，文中结合标准化后的岭迹图与标准化后的方差膨胀因子选择k。若采用方差扩大因子法，当k≥0.016时，方差扩大因子小于10，故建议在此范围内选取k。同时结合岭迹图法选取k=0.016。

在用岭回归进行变量选择时发现，解释变量x4有相对稳定且绝对值较小的岭回归系数，可以剔除该变量。又因为x2，x3，x6和x9的岭回归系数很不稳定，且随着k的增加很快趋于0，这些自变量也是可以剔除的。最终剩余变量为x1，x5，x7，x8，即可用这些变量建立回归方程。

当k=0.016时，选模型标准化岭回归方程为：

0.36x7+0.064x8

(13)

岭回归模型均方误差RMSE=0.130 38。相比于表6逐步回归后选模型下的均方误差，虽略有增大，但属于可接受范围内。造成这种情况的原因是在岭回归最优子集筛选时存在一定人为主观因素，相比于逐步回归筛选更为活跃，因此可能导致均方根误差的变化。宏观上讲，岭回归模型的建立也是成功的，它同逐步回归下box-cox模型一样，能够解决多重共线性问题。

4 模型拓展

文中虽已经得到了较为完善且结果良好的模型，但仍需探讨模型所存在提升的空间。散点图矩阵如图1所示。

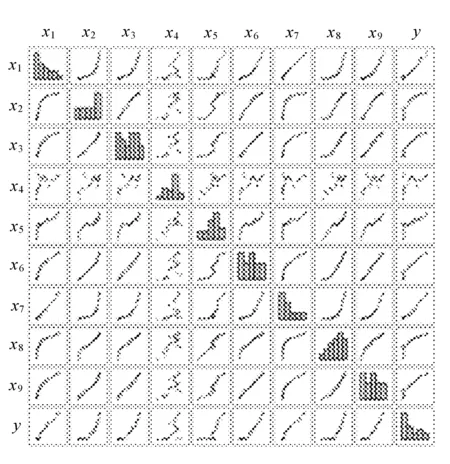
图1 散点图矩阵

由图1可见，y与部分解释变量存在着较为明显的曲线走势。如y与x2，x3等解释变量大致为指数函数形式。从社会意义方面考虑，指数也是更符合随稳定年增长率而增长的粗离婚率现象[8-9]，以x2为例可以假设存在关系。

y=exp(β0+β1x2)

(14)

基于这种思想，尝试将对因变量y进行一步对数变换，再进行普通最小二乘回归。将因变量y进行对数变换，得到新变量yt，即有关系

yt=ln(y)

(15)

此时基于变换后的yt进行全模型普通最小二乘回归，分别见表11和表12。

表11 非线性回归方差分析

表12 非线性回归拟合优度

与普通最小二乘全模型相比较，非线性回归模型均方根误差从0.061 38减小为0.043 77，体现了非线性模型的稳定性与优越性，这说明了对因变量y的对数变换是合理的，提高了方程的拟合程度。若想更为精确的拟合问题，可以选择在对数变换基础上进行后续多种方法的回归分析。

5 结论与建议

在研究单一因变量y的过程中，首先根据模型变量之间的关系、误差项之间的关系，针对模型存在的异方差和自相关现象进行了诊断与消除。其次针对模型多重共线性问题使用逐步回归法进行消除，并以岭回归法作为参考[6]。最终建立了逐步回归模型、岭回归模型，均得到了拟合度高、实际意义清晰的模型。两个模型虽形式上各有不同，但纵观其反映的社会问题大同小异。文中采用拟合程度最高且有代表性的box-cox变换逐步回归模型(12)为文中最终结论。

显然，此模型的意义符合实际情况，影响回归方程的变量为x1、x3、x5。x1与y的正相关系数说明随着社会经济水平的进步，离婚率会随之增加。但因x1只是经济水平的一个宏观体现，并不能完全概括社会的经济水平。所以对y的影响率较低，x1每增加一个单位,y会增加0.000 1。反观x2并未入选模型，可以认为与其说受教育水平对离婚率有所影响，不如说学历高低会对离婚率产生影响。而代表社会服务业水平的x5也入选了模型，符合社会服务业发展对人民生活及思想的影响。

宏观来讲，y受到经济因素、教育水平因素以及社会因素三个方面的影响。首先，随着社会的进步、经济水平的不断提升，离婚率也会随之增加。其次，高学历人群的婚姻相比低学历更为稳定。最后，社会的变迁对人民婚姻情况也有所影响，伴随着社会第三产业也就是服务业水平的提升，婚姻却变得更为脆弱。

鉴于以上分析，为稳定全社会婚姻的稳定性，文中提出如下建议：

随着社会主义市场经济的不断推进，传统的伦理道德受到冲击，新的伦理道德观念还未建成。我国人民对婚姻的看法应从根本上实现转型，摆脱老旧的封建思想如童养媳、门当户对、重男轻女，也不该不经筛选地效仿外来文化如AA制婚姻、性解放、三八界限婚姻。结合文中回归模型与社会情况，当下常出现将择偶价值观建立在高强度经济基础上的情况，这种趋势是病态的、不被接受的。显然，与基于爱情婚姻相比，建立在经济水平上的婚姻是不稳定的。由此呼吁我国社会建设健康积极的婚姻观念、择偶观念以及婚后生活观念，以减少大批量离婚对社会带来的不稳定性。

参考文献：

[1] 俞文书.少数民族地区族际离婚的特点及原因研究[J].怀化学院学报,2016，35(1)：61-65.

[2] 解韬.我国成年残疾人口的婚姻状况及其影响因素研究[J].人口学刊,2014，36(4)：54-63.

[3] 杨文山.台湾地区的婚姻挤压[M].北京：中国人口出版社,2005.

[4] 李银河.当代中国人的择偶标准[J].中国社会科学,1989(4)：61-74.

[5] 冯虹,赵一凡,艾青.中国超大城市新生代农民工婚姻状况及其影响因素析:基于2015年全国流动人口动态监测调查数据[J].北京联合大学学报,2017(1)：63-69.

[6] 何晓群,刘文卿.应用回归分析[M].4版.北京：中国人民大学出版社,2015.

[7] 孙建英.概率论与数理统计中的数学建模案例[J].长春工业大学学报:自然科学版，2014，35(2)：224-226

[8] 薛菁.进城务工对农民工婚姻生活影响研究[J].科学·经济·社会,2013，31(3)：148-152.

[9] 祝平燕,王芳.返乡相亲：新生代农民工的一种择偶形态-以豫东S村为例[J].中国青年研究,2013(9)：51-60.