三次B样条有限体积元法

秦丹丹， 冯 雪， 申延成， 黄文竹

(1.空军航空大学 基础部， 吉林 长春 130022；2.贵州医科大学 生物与工程学院， 贵州 贵阳 550025)

0 引 言

由于B样条函数是对称单峰值函数，并且具有光滑性好、紧支集等特点，在插值逼近和微分方程求解问题中有广泛应用。B样条函数的光滑性要优于Lagrange和Hermite型样条函数，并且以B样条为基函数的有限元空间只有一组基函数，而Lagrange和Hermite型有限元空间都是两组基函数,因此，在微分方程的数值计算中，B样条函数是值得研究的。以B样条为基函数的有限体积元法生成的刚度矩阵是稀疏的，并且有对称性和正定性，便于计算实现。可以说，B样条有限体积元法兼具差分法和有限元法的优点。基于以上考虑，文中构造了三次B样条有限体积元法。

1 B样条的定义与性质

B样条函数有多种定义方法，文中介绍两种。文中m和n都是正整数。

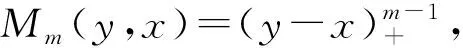
Mm(x)=Mm[xj,xj+1,…,xj+m;x]=

称Mm(x)为关于节点xj，xj+1，…，xj+m的m阶m-1次B样条函数[1]。

文中用到的等距B样条函数与定义1有所不同，按照下面的递推关系式给出。

定义2m阶B样条的卷积定义式[1-2]：

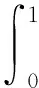
m≥2,

其中

由定义1和定义2得知，两种定义之间可以相互转化。

由定义2能够推出m阶B样条的相关性质：

1)正定性与紧凑性，Sm(x)≥0，具有紧支集[0,m]；

2)分段光滑性，Sm(x)是一个分段m-1次多项式，Sm(x)∈Cm-2(-,)；

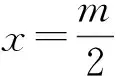
4)成立积分递推式

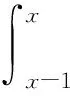
及代数递推式

其中，m=1,2,…。

B样条还具有许多优良性质[2]。

根据定义2可以计算出三次B样条的表达式：

2 基于B样条的有限体积元法

考虑两点边值问题：

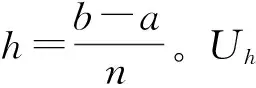
i=-3,-2,…,n-1。

为方便处理强加边值条件，将前三个函数换成线性组合[3-5]：

6φ-3(x)，

φ-2(x)-4φ-3(x)，

同时将最后三个基函数也换成线性组合：

φn-2(x)-4φn-1(x)，

6φn-1(x)。

改换前后两个空间是等价的。任一uh∈Uh可以表示成

其中，j=0,1,2,…,n。

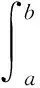
a(uh,vh)=(f,vh),

∀vh∈Vh。

a(u,v)是对称正定的双线性形式，变分形式有唯一解。

两点边值问题的积分守恒形式为:求uh∈Uh，使得

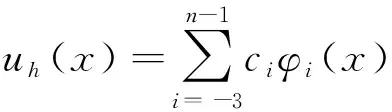
uh(xi)=ci-3φi-3(xi)+ci-2φi-2(xi)+

ci-1φi-1(xi)

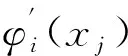
需要指出，若用Hermite型三次元求解两点边值问题，刚度矩阵的带宽为7，与三次B样条有限元是一样的。但Hermite型三次元在每个节点有两个参数，B样条有限元在每个节点只有一个参数(不计边界以外的扩充点)，所以，若用相同的节点个数，两种方法的系数矩阵阶数之比约为2∶1，而二者的收敛阶却相同。从这点来看，B样条有限元法更有优势。

3 数值算例

取a=0，b=1，p=0，f(x)=4π2sin(2πx)，两点边值问题的精确解为u(x)=sin(2πx)。用MATLAB编程得到数据见表1。

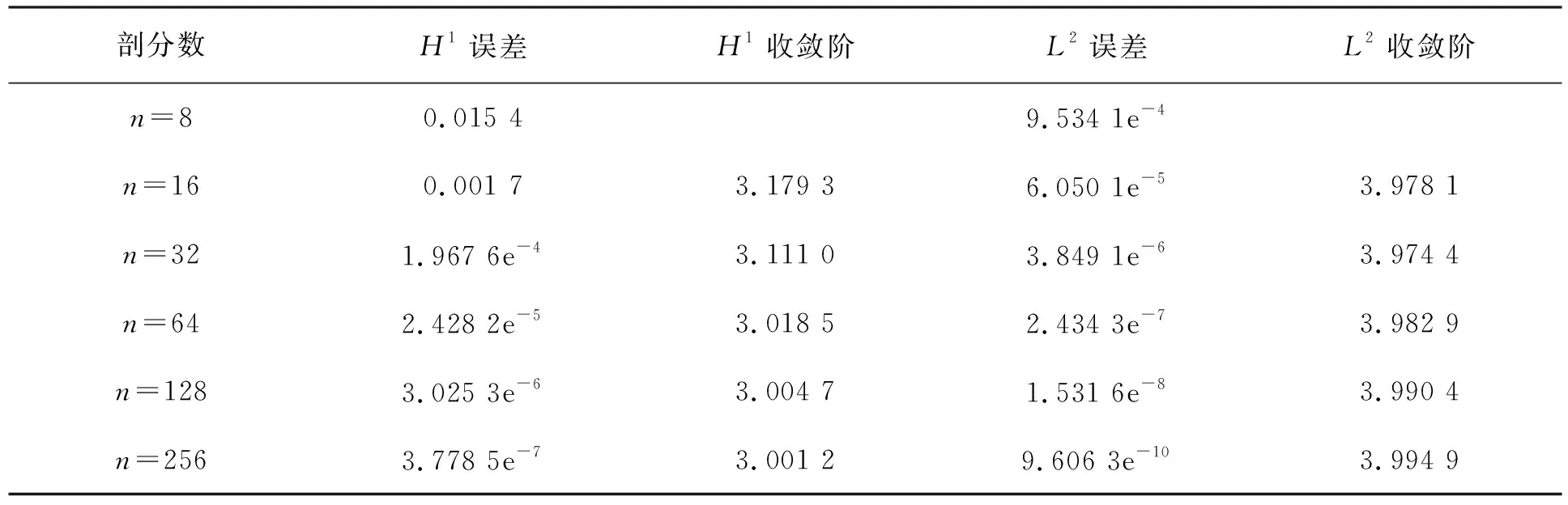
表1 三次B样条有限体积元法的误差与收敛阶

4 结 语

构造了基于三次B样条的有限体积元法，该方法有很好的收敛性。在H1半模和L2模下，三次B样条有限元法分别具有3阶和4阶收敛精度，三次B样条有限元法具有最佳L2收敛阶。我们发现B样条有限元法与传统有限元法一样有较高的收敛阶，还具有一些优于传统有限元法的性质。

参考文献：

[1] 孙家昶.样条函数与计算几何[M].北京：科学出版社，1982.

[2] 陈广生.B样条函数的一个性质[J].广西科学，2008，15(4)：381-382.

[3] 石钟慈.样条有限元[J].计算数学，1979(1)：50-72.

[4] 梁旭彪,简柏敦，倪光正.B样条有限元[J].中国电机工程学报，1987(6)：11-22.

[5] 李荣华,冯果忱.微分方程数值解法[M].北京：高等教育出版社,1995.

[6] Ronghua Li， Zhongying Chen， Wei Wu. Generalized difference methods for differential equations [M]. [S.l.]: Marcel Dekker，Inc.，2000.

[7] Wang Tongke. High accuracy finite volume element method for two-point boundary value problem of second order ordinary differential equations [J]. Numer Math.， Journal of Chinese Univ.，2002，11(2):213-225.

[8] Z Cai. On the finite volume element method [J]. Numer. Math.,1990,58(1):713-735.

[9] Ronghua Li. Generalized difference methods for two point boundary value problems [J]. Acta Sci. Natur Univ. Jilin,1982(1):26-40.