未知协方差条件下的VSSI T2控制图的经济性设计

顾丽君，唐庆国

（南京理工大学 经济管理学院，南京 210094）

0 引言

自从1947年，Hotelling提出了第一张均值向量T2控制图之后，多元统计质量控制便进入了人们的视野。现代产品指标多样，且关系复杂，多变量控制图更加符合生产的需求。

与单变量控制图相同，大多数多元均值向量T2控制图是在协方差已知且保持不变的前提之下讨论对均值的控制。但在实际生产中，协方差并不是一成不变的。一些学者进而研究了多变量协方差控制图[1-3]，如 ||S图、W图、L图等。但是这些控制图存在明显的缺陷，即要求“协方差已知”，这在实际生产控制中是十分苛刻的。

本文结合经典经济模型研究了未知协方差矩阵的多元T2控制图的经济性能。利用数值实例，对其灵敏度进行分析，为企业参数的选择提供依据和建议。

1 总体协方差未知的VSSIT2控制图

假设产品有p个质量特征，产品质量特征X服从均值向量为μ，协方差矩阵为Σ的p维正态分布。Xij'i=1'…'n(i)'j=1'...'m为来自X的第i个样本子组，m表示子组容量，Xˉi表示子组 i的均值向量，即假设过程中只受到一个异常原因的影响，使得过程均值从μ0偏移到 μ1，μ0是目标值，则T2控制图统计量为：当总体的协方差矩阵 Σ 未知时，需要利用已有的样本数据估计Σ。式中的μ0和Σ需要用各子组均值向量的平均向量Xˉ和各子组协方差矩阵的平均值SP代替其中Si为子组i的协方差矩阵。假设用来建立控制图的n个子组均为受控的子组，则和SP均为 μ0和Σ的无偏估计。构造T2控制图统计量为-Xˉ)。

此时服从第一自由度为p，第二自由度为(n-p)的F分布[4,5]。即

对于VSSIT2控制图，假设抽样间隔为(h1'h2)，h1＞h2；抽样大小为 (n1'n2)，n2＞n1；警戒限为ω，大小不变，k为控制限。于是控制图可分为以下三部分：I1=[0'ω]；I2=[ω'k]；I3=[k'+∞)。当取样落在受控区域时，则下一次取样的参数选取如下：

当则判定过程失控。

2 衡量指标

通常衡量控制图性能的指标主要有三个：ATS（平均运行时间）；ANOS（整个周期的平均检测数）；ANF（平均误报次数）。未知协方差控制图的研究目前仅局限于概率分布研究，并没有考虑其经济性设计，也没有将其与动态控制图结合起来。本文用马尔科夫链预测法研究VSSI控制图的统计性指标，同时对其经济性进行了设计和分析。

设受控状态为I，失控状态为N，本文一共构建了6个马尔科夫链状态空间

假设异常原因发生的时间服从参数为λ的指数分布，那么异常原因发生的概率为1-e-λhi'i=1'2。当过程处于状态{I 3 'I}时，属于误报警；当过程处于状态{I3'N }时，即为吸附态。则该过程的转移概率矩阵为：

其中Pij表示从状态i转移到状态j的概率：

对于评判控制图的指标，计算公式如下：

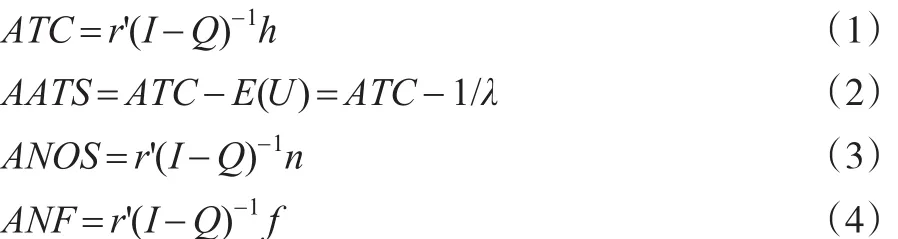
其中，h为各个状态对应的样本间隔，r为过程的初始概率，f为各个状态对应的误报警概率，n为各个状态对应的样本大小。为避免生产最初就存在问题，本文中取（r'为r的转置，其他同理）：

3 数值实例

每个生产周期都包含了受控阶段、失控阶段、检测阶段和维修阶段。关于费用函数，已有不少的经典模型。本文中的费用函数引用Costa经济性设计模型[6]。

式（5）中V0表示受控状态下每小时的利润；V1表示失控状态下每小时的利润；C0表示单个抽样的成本；C1表示误报警时的平均搜索费用；A1表示搜索纠正异常原因的平均费用；T0表示搜索误报警的平均时间；T1表示搜索纠正异常原因的平均时间。

结合数值实例研究VSSIT2控制图的统计性和经济性，本文取p=2，式（5）中的参数选取为：λ=0.01,T0=1.5h,T1=1.5h,C0=3.6元/个 ，C1=115元/次 ，A1=465元/次 ，V0=135元/次，V1=60元/次。控制图的设计参数如表1所示。

表1 控制图的设计参数

当n=4时，～3F(2'2)，即1/3服从第一自由度和第二自由度均为2的F分布；当n=6时，0.4服从第一自由度和第二自由度分别为2和4的F分布。基于以上参数，可以推导出矩阵P中的元素。例如：

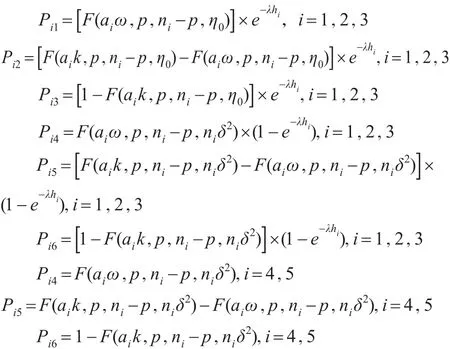
其中F(x'p'n-p'η)表示非中心F分布的累计概率分布函数，p为第一自由度，n-p为第二自由度，η为非中心参数。 η0=0，ηi=niδ2，δ为中心从 μ0偏移到 μ1的马氏距离。a1=a4=1/3，a2=a3=a5=0.4。经计算，VSSIT2控制图的统计性和经济性指标如表2所示。

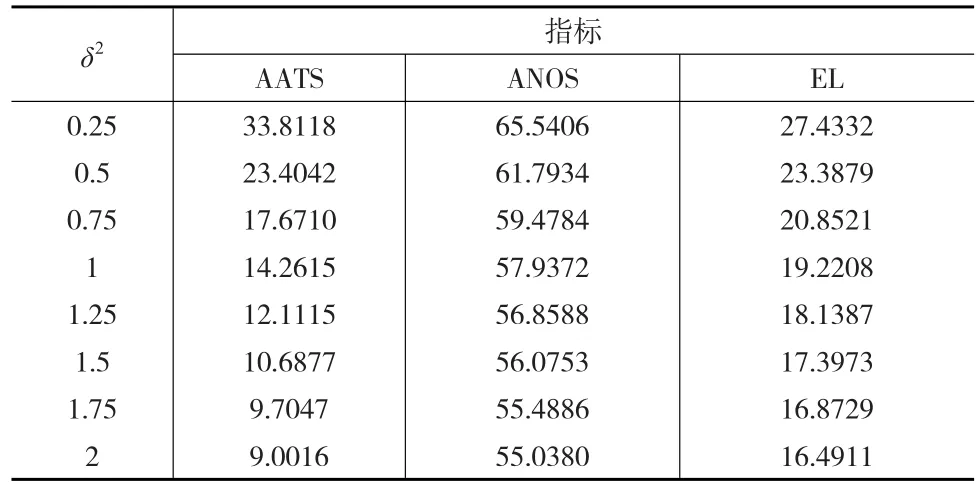
表2 VSSIT2控制图的统计性经济性指标

由表2可以看出，其统计性和经济性指标基本符合该控制图的一般规律。随着δ2的不断增大，AATS、ANOS和EL的值都不断减小，且减小的频率越来越小。即过程偏移较大时，VSSIT2控制图发现异常的速度较快，且成本较小。

假定过程的偏移为δ2=0.5，运用Matlab软件中的optimtool的遗传算法工具箱来搜索控制图经济性设计的最优解，以便相应的单位时间损失EL达到最小值。考虑到实际情况和计算简便，求解下面的最优化问题：

minE(L)(n1'n2'h1'h2'w)

约束：0＜n1＜n2＜20'ni为整数

20＞h1＞h2＞0

0＜ω＜k

得到控制图的最优参数及其EL值如表3所示。

表3 VSSIT2控制图的优化参数

4 灵敏度分析

为了研究其他参数（如 δ、V0、V1）对EL值的影响，本文结合因子分析方法，三个参数各取两水平，即作三因子两水平23的全因子试验设计。参数的两水平选取如表4所示，该试验设计的运行顺序和该条件下优化的结果如表5所示。

表4 三个参数的两个水平

表5 全因子试验设计及优化结果

对于每个试验子组，都用Matlab里的遗传算法工具箱求得最优解。根据上表数据，可研究表中的参数对VSSI T2控制图经济性设计的影响作用。

本文采用Minitab软件针对上述三个参数作方差分析，得到主效应图（见图1）、效应排列图（见图2）和方差分析结果（见表6、表7）。

图1 三个参数对EL值的主效应图

由上述图表可得以下结论：V1越大，V0越小；δ2越大，EL值越小，生产过程中造成的利润所失越小。A、B、C三个因子（V1、V0、δ2）对EL均有显著影响，另外 δ2和V0的交互作用对其也有显著影响。从方差分析可以看出δ2、V1、V0的P-Value均小于0.05，可见其确实显著影响了利润所失的大小。结合实际生产情况，可以得出：在不影响正常生产的情况下，受控时利润和失控时利润接近，VSSIT2控制图检测大偏移时，利润所失更加小。

5 总结

多元T2控制图被广泛应用于监测多元质量问题，而VSSI控制图已经被证明在检测微小偏移时性能明显优于一般控制图。本文研究了未知协方差的VSSIT2控制图，基于已有的研究成果，结合马尔科夫链方法，推导出了转移概率。通过数值实例，计算了在不同偏移下控制图的统计性和经济性指标。利用遗传算法确定了利润所失最小化时控制图各参数的取值。最后，结合全因子试验设计，分析了模型参数等对EL值的影响效应。通过分析发现，各参数对利润所失均具有显著影响。受控时利润与其正相关，失控时利润和偏移大小均与其负相关。因此，在实际生产中，需要根据需求选择合适的参数值。

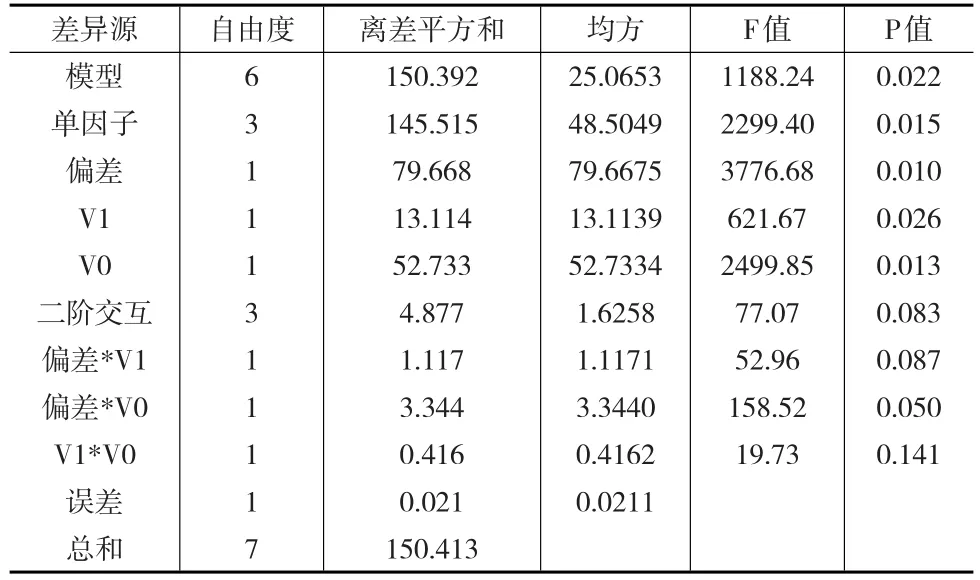
表6 各因子的方差分析

表7 模型概述

[1]刘艳永,张公绪,孙静.基于最大、最小特征根的多元协方差控制图[J].方法与应用,1998,(6).

[2]赵永满.基于威沙特分布的二元过程均值与协方差监控[J].统计与决策,2015,(5).

[3]Chou C Y,Chen C H,Chen C H.Economic Design of Variable Sampling Intervals T2Control Charts Using Genetic Algorithms[J].Expert Systems with Applications,2006,(30).

[4]Robert L,Mason,Nola D.Decomposition of T2for Multivariate Control Chart Interpretation[J].Journal of Quality Technology,1995,(27).

[5]Hayter A J,Tsui K L.Identification and Quantification in Multivariate Quality Control[J].Journal of Quality Technology,1994,(26).

[6]Maysa,Costa.Economic-Statistical Control Chart Design:A Sensitivity Study[J].Brazilian Journal of Operations&Production Management,2005,10(2).