混频数据抽样模型等权低频化处理的估计偏误研究

王春枝，穆 楠，赵国杰，于 扬

（1.内蒙古财经大学 统计与数学学院，呼和浩特 010070；2.天津大学 管理与经济学部，天津 300072）

0 引言

混频数据抽样模型(Mixed Data Sampling，简记为MIDAS)近年来得到了学界的广泛关注，其主要思想是利用比较容易观测到的高频率数据来预测不容易观测到的低频率数据，但是由于数据频率的差异，在参数估计方面存在较大的难度。早期，学术界对于此问题的处理，主要采用两大类方法：插值法和桥接模型法。桥接模型法的本质和插值法是一样的，二者都是建立在依时性加总思想基础之上。此外，还有一些学者直接采用其他频率相同的指标来近似代替低频指标进行量化分析。Amemiya和Wu（1972）[1]利用处理非平稳时间序列的ARIMA模型以及单位根检验的ADF方法，对比分析了插值法、桥接模型等方法的适用性以及有效性，对比分析的结果表明这类依时性加总的处理方法对信息的利用并不充分，因为各种频率的数据都蕴含其独有的信息和趋势，将不同频率数据转化为同一频率数据的处理方式造成了高频数据信息损失，降低了模型精度。在这样的背景下，对不同频率的混合数据进行直接建模的混频数据模型便应运而生[2-4]。GDP相关性较高的CPI等指标的月度数据实时预测了季度GDP数据，这是混频数据直接应用的开端，为混频数据抽样模型的广泛应用奠定了基础。

Ghysels等(2004)[5]在Koenig[4]研究的基础上，构建了考虑数据非平衡性的混频数据抽样模型（MIDAS），其主要思想是根据数据特征构建不同的权重多项式，将高频和低频指标结合，从而可以动态地考察不同频率指标之间的关系。此后，MIDAS模型在金融、宏观经济领域得到普遍应用，越来越多的研究成果将高频数据加入到低频宏观经济变量预测模型中，并取得了极大成功，这些成功的案例均表明高频变量和低频变量直接应用能够显著提高模型的预测精度[6-9]。

纵览相关成果，当前关于MIDAS模型的研究主要基于实证角度进行，重在运用MIDAS模型对经济现象进行定量分析与预测，尚缺乏从理论角度探讨其与经过转换的传统同频率模型之间内在关系的研究，对其估计量的统计性质也缺乏相应的数理证明。鉴于此，本文从MIDAS模型的构成形式出发，通过对高频变量的成分进行分解，从而将MIDAS模型与传统处理混频数据的方法进行比较，传统的混频数据处理的主要思路是赋予高频变量均等化的权重将其转换为低频变量，得到EQW（Equal Weights）模型。在此基础上，进一步从数理统计的角度对EQW模型参数的普通最小二乘估计量（Ordinary least squares，简记为OLS）的统计偏倚性和有效性进行推导，得出其偏倚为零的约束条件，以期为MIDAS模型在实时预测的精度保证方面提供理论支持。

1 MIDAS模型的EQW导出

1.1 一元混频数据模型（MIDAS）及其分解

首先，以一元混频数据模型为例，设变量Yt是模型的被解释变量（因变量），具有低频属性，下标t代表所考察的时期。一元混频模型中只含有一个高频解释变量（自变量），记为，其中m为高频数据的个数，时间区间为第t期到t-1期，m实际上就是高频变量与低频变量的频率的倍差。记q代表模型中滞后变量的滞后阶数，则一元混频模型（MIDAS）的函数方程可以写为：

式（1）中，ωi(θ)是赋予目标参数θ向量的一个权重函数，并且满足权数之和等于1的统计要求，即L为模型中的延迟算子，其满足条件是除之外其他影响被解释变量Yt的随机干扰项，满足零均值、同方差、无自相关、与解释变量不相关等古典假定，并且 μt～N(0'σ2)。

令代表高频解释变量与低频被解释变量的频率倍差m内的所有样本数据个数经过等权重平均得到的指标，即有：

根据式（2），经典的同频EQW回归模型可表示为：

设qm=m-1，则式（1）可以转化为：

进一步展开得到具体形式为式（5）：

令(θ)为高频解释变量按照不等权重进行加权平均的权重函数，则将其带入式（5），可以得到：

即：

同理，当qm＞m-1时，最高滞后阶数设为qm，式（1）可分解为：

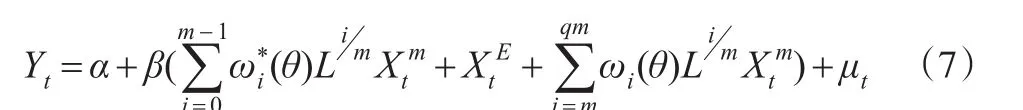
从上述分解过程中可以清晰地看到一元MIDAS模型与EQW模型之间的关系，观察式(6)和式（7）可以发现：一元MIDAS模型的解释变量部分既包含了传统的按等权重平均进行数据处理的部分同时也包含了独立引入权重函数ωi(θ)的加权平均部分这意味着通过赋予高频变量均等化的权重将其转换为低频变量得到的EQW模型只是一元MIDAS模型的一个组成部分，EQW模型损失了模型中高频解释变量的一部分信息是显而易见的[10]。

1.2 多元混频数据模型（M-MIDAS）及其分解

接下来，将MIDAS模型中的高频解释变量扩展至一般情形，令为k个同频的高频解释变量，其函数表达式记为为模型中高频解释变量的个数，且 j=1'2…k。另外，设q为模型中高频变量的最大滞后阶数，从而多元混频数据模型M-MIDAS的方程形式可以表示为：

式（8）中，m1'm2'…'mk代表了k个高频解释变量的频率，不同解释变量的频率既可以相等也可以不相等，另外，记为每个高频解释变量的滞后阶数，一般情况下，认为这些高频解释变量的滞后阶数是相同的，即同步变化性，令表示高频解释变量的权重函数，其满足权重函数之和为1的统计要求。

当 j个高频解释变量的频率满足m1=m2=…=mk=m，即频率都相同时，第 j个高频解释变量的等权平均的部分可表示为同理，设qm=m-1，多元混频数据模型M-MIDAS可转化为:

式（9）中

如果 j个高频解释变量的频率m1'm2'…'mk至少一个不同时，权重函数方程的表达式调整为

设qm＞m-1，模型中高频变量的最大滞后阶数设为qm，根据同样的思路，可将式（7）进一步变形为：此时，多元混频数据模型M-MIDAS的方程形式就可表示为：

根据式(10)和式（11）可以看到，在 qm=m-1和qm＞m-1两种情形下，多元混频数据模型M-MIDAS均可以分解为两部分：按等权重平均处理的部分、独立引入权重函数的加权平均部分。由此可得与一元混频数据模型MIDAS同样的结论：简单地将高频解释变量等权低频化处理的多元EQW模型仍然不可避免的损失了一部分高频解释变量自带的信息。

1.3 非限制性多元混频模型（U-M-MIDAS）及其分解

式（1）和式（8）在分解时，都施加了约束条件：所有高频解释变量的各个滞后项权重函数ωi(θ)的和等于1，当解释变量与和被解释变量的频率倍差较小时，并且所需要估计的参数个数较少时，可以放松对权重函数之和为1的约束条件，选择非限制混频数据回归模型U-M-MIDAS对低频被解释变量进行回归，借鉴分布滞后回归模型，对高频解释变量不赋予权重，则可得非限制混频数据回归模型的方程形式为：

其中 Φ(L)和 β(L)为算子-φpLp，回 归 系 数的白噪声序列。

首先，假设qm=m-1的情形下，按照与前文同样的方法，式（12）可以分解为：

其中回归系数

当qm＞m-1时，假设式（12）中，所有高频解释变量的最高滞后阶数为qm，据此，式（12）可分解为：

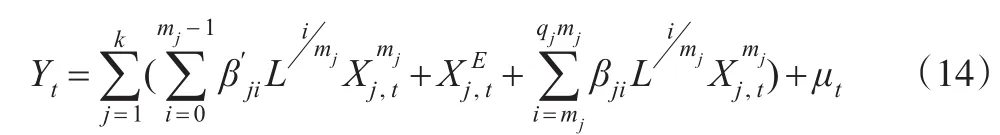
观察式(13)和式（14）同样可以发现，等权低频化处理的部分Xj'E

t只是非限制混频数据回归模型U-M-MIDAS的部分构成，而U-M-MIDAS模型其余部分所携带的信息，EQW模型是无法体现的。

综上，通过对三种基本形式的MIDAS模型按等权重和非等权重分解高频回归元数据集，可以清晰地看到MIDAS模型与EQW模型的区别及内在联系，也均证明了MIDAS模型进行直接的等权低频化处理，会造成高频变量本身携带的信息损失，这种信息损失，会给模型的估计量带来什么后果？这也是本文接下来要研究的另一个问题。

2 EQW模型OLS估计量的偏倚性

本文以多元混频模型（M-MIDAS）为例，从估计量的偏倚角度，探讨M-MIDAS模型直接等权低频化处理得到的EQW模型，在损失信息的情况下如何影响模型参数估计的统计性质。

将式（8）的多元混频模型由代数形式改写为矩阵形式：

同样地，假设所有高频解释变量的频率一致，此时随机过程满足：

其中，j为高频解释变量个数，j=1'2'…'k，q为高频解释变量最高滞后阶数。ωij(θj)为关于权重参数向量θj的权重函数，满足条件ωij(θj)∈[0'1]，定义变量：

假设被解释变量与解释变量之间真实的函数关系为式（8），其中高频解释变量Xt(θ)可以表示为两部分：等权重加权部分和非等权重加权部分(θ)，即 Xt(θ)满足等式从而式（15）的矩阵形式进一步转化为：

其中随机项ut服从正态分布。(θ)是一个对角矩阵，其对角线元素为且

假设q=m，在模型中加入自回归项，得到混频数据自回归模型AR-M-MIDAS形式如下：

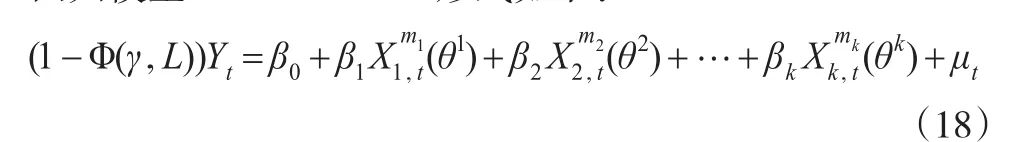
其中依据式（18）建立经典回归模型为：

其中

对式（19）的回归模型利用普通最小二乘法（OLS）进行回归，得到参数估计量的表达式为：

将式（18）带入式（20），可得：

其中所以EQW模型的普通最小二乘估计量的偏度可表示为：

观察式（22）可以看到，只要ψ(θ)≠0，EQW模型的普通最小二乘估计量的偏倚就不为0，这意味着偏误的存在。只有当与满足即

与为正交关系，则 E(β̂*)=β 成立，此时，EQW模型的OLS估计量才具有无偏性。

3 EQW模型OLS估计量的有效性

良好的统计量的另外一个性质是有效性，主要考察估计量的方差。接下来，本文对EQW模型和多元混频M-MIDAS普通最小二乘估计量的渐进分布以及渐进有效性进行对比分析。首先，定义关于参数β和θ的参数空间为Φ=(β'θ)，定义模型的两个组成部分：等权处理与非等权处理的总体均值为：

设导数存在，从而普通最小二乘估计量可表示为：

对式（24）移项并进一步整理，可得：

根据逆矩阵是关于原始矩阵的一个连续函数的数学性质，令 plim(X'Xn)-1=Q-1，同时，根据林德伯格—费乐中心极限定理可以得到：

由式（26）的极限分布为σ2Q-1)。

记

因为等式成立，所以M-MIDAS模型中参数估计量̂的方差为：

如果令

则

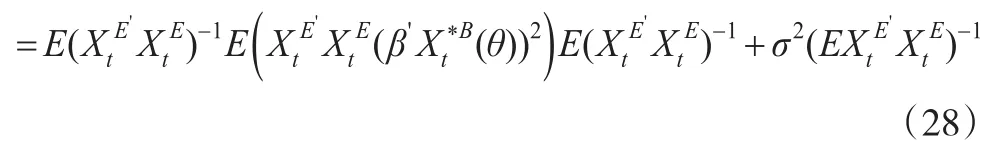
从而̂的均方误可表示为：

而多元混频模型的OLS估计量̂的均方误为:

比较式（29）和式（30），可以得到两个结论：

（1）当 θ=0,且时，

（2）当 θ=0,而时，由于所以有此时是比β̂更有效的一个估计量。

本文进一步分解混频模型，探索EQW模型普通最小二乘估计量与频率倍差m的关系。设为一个独

立同分布的随机过程，并且满足条件

设为MIDAS模型等权重的均值,其

非线性部分记为：

则只有一个独立同分布回归元的MIDAS模型可表示为：

因为所以成立。由前文可知，EQW模型的OLS估计量的偏倚为则：

结合式（27）可得：

由式（34）可以看到，将高频解释变量等权低频化处理得到低频数据，并将其应用于传统回归模型，按照普通最小二乘法进行拟合，得到的参数OLS估计量β̂*的方差与频率倍差m呈同方向变化的关系，高频解释变量与低频被解释变量的倍差m越大，β̂*的方差也越大，统计量β̂*的有效性也随之不断降低，这对模型而言是一个严峻的挑战：首先，从模型检验层面看，建立在估计量的方差基础之上进行的假设检验，如回归系数的显著性检验、回归方程的显著性检验等，其检验的信度都会降低；其次，从模型应用的层面看，被解释变量与解释变量之间关系的结构分析、被解释变量未来取值的预测等常见的模型应用都将面临精度下降的问题。

4 结论

本文依据高频数据低频化的常用变换方法，将三种基础类型的MIDAS模型从内部结构上进行分解，结果发现将高频数据直接等权低频化处理的EQW模型损失了MIDAS模型的非等权重加权平均部分。进而，本文通过数理推导，从估计量的偏倚性以及有效性角度证明了EQW模型OLS估计量的统计性质。结果表明：EQW模型由于信息损失会导致回归系数估计时产生偏倚，只有当等权重加权平均部分和非等权重加权平均部分(θ)正交时，偏倚才会为零；EQW模型OLS估计量的方差与频率倍差呈同方向变化的关系，高频解释变量与低频被解释变量时间频率的倍差越大，估计量的有效性越低。

[1]Amemiya T,Wu R.The effect of Aggregation on Prediction in the Autoregressive Model[J].Journal of the American Statistical Association,1972,67(339).

[2]Zadrozny.Gaussian Likelihood of Continuous-time ARMAX Models When Data are Stocks and Flows at Different Frequencies[J].Econometric Theory,1988,4(1).

[3]Zadrozny.Estimating a Multivariate ARMA Model With Mixed Frequency Data:An Applicationto Forecasting US GNP at Monthly Intervals[R].Federal Reserve Bank of Atlanta Working Paper Series,1990.

[4]Koenig E F,Dolman S,Piger J.The use and Abuse of real-time Data in Economic Forecasting[J].Review of Economics and Statistics,2003,85(3).

[5]Ghysels E,Santa-Clara P，Valkanov R.The MIDAS touch：Mixed Data Sampling Regression Models[R].Working Paper,Anderson School of Management,UCLA,2004.

[6]Götz T B,Hecq A,Smeekes S.Testing for Granger Causality in Large Mixed-frequency VARs[J].Journal of Econometrics,2016,193(2).

[7]刘汉,刘营,王永莲.经济景气指标与实际GDP增长率的混频预测[J].统计与决策,2017,(21).

[8]Li X.A MIDAS Modelling Framework for Chinese Inflation Index Forecast Incorporating Google Search Data[J].Electronic Commerce Research and Applications,2015,2(14).

[9]Smith P.Google's MIDAS Touch:Predicting UK Unemployment With Internet Search Data[J].Journal of Forecasting,2016,35(3).

[10]于扬.混频数据回归模型的建模理论、分析技术研究[D].大连：东北财经大学硕士论文,2016.