非平稳面板数据共同因子与结构变化的交互效应探讨

陈海燕

（重庆工商大学 长江上游经济研究中心，重庆 400067）

0 引言

2005年以来，以面板单位根检验和面板协整检验为主体的非平稳面板数据建模已成为计量经济学实证研究的主要分析方法之一。以“面板单位根检验——面板协整检验——面板协整模型估计——面板误差修正模型”为基本研究范式，在经济、社会、金融、贸易、教育、能源等各方面均得到了广泛地应用和深入分析。早期的非平稳面板数据建模假定模型满足同方差、无序列相关、无结构变化、无截面相关等假设条件，第一代的面板单位根检验和协整检验均假设截面独立和无结构突变[1]。但是，经典假设往往是最理想的状态，并不能完全满足现实问题分析需要。由于面板数据具有时间和截面的双重特征，一般表示为(i,t)双下标形式，不同的变量可以记为 yit、xit、zit等。所以，面板数据具备时间序列数据可能存在的序列自相关和结构变化特征，也会有横截面数据可能存在的异方差性。同时，面板数据的截面个体之间还可能存在截面相关，以及与截面相关具有交互作用的结构变化。违背经典假设的序列自相关和异方差性的检验与修正方法在时间序列数据和横截面数据研究中已比较成熟，在面板数据分析时可以直接借用[2]。但是面板数据的截面相关及其与结构变化的交互影响尚待进一步研究。由于共同因子结构是面板数据截面相关最常用也是最易处理的表现形式，所以本文中截面相关主要以共同因子结构来体现。

理论方法研究中，诸多文献是将截面相关和结构变化的处理与单位根检验或协整检验一同进行的，即是在构建非平稳面板数据模型检验统计量的同时，通过某种方式消除了共同因子或结构变化的影响，并通过大量模拟论证了检验方法的稳健性[3,4]。但是，实证研究中面对的是实际客观数据，最优的模型形式需要经过多重检验才能获得，直接套用已有模型将导致估计结论无效，这也是诸多文献中提及的计量经济模型无为表现的原由之一：理论构建与实证应用逻辑上的差异导致经济问题分析产生了伪结论。那么面板数据是否存在截面相关或结构突变，以及是以怎样的形式存在都将影响最优模型的选择过程，影响最终的分析结论。因此，在实际问题研究中应当首先通过恰当的方法去确定面板数据的基本结构，以构建最适宜的模型形式。王珂英和张鸿武(2016)[5]、王维国等(2013)[6]在构建非平稳面板数据模型之前首先就考虑了共同因子和结构变化，并采用了适宜的方法予以论证，但是在处理结构变化和共同因子时往往是将此两种情形分别进行检验和处理，均未考虑二者之间的交互影响效应。

当面板数据存在共同因子时，每个截面个体的结构变化可能会因为其他截面的变化而发生改变。那么，共同因子的存在是否会改变横截面个体的结构变化？基于这样的考虑，本文在对已有的面板数据截面相关和结构变化检验方法进行分析的基础上，给出非平稳面板数据模型中截面相关与结构变化交互影响的实证分析结果，为采用基本研究范式进行实证提供前期参考，为非平稳面板数据模型的深入发展呈现新的思路。

1 共同因子结构检验

对于存在截面相关的非平稳面板数据模型，忽视截面相关将导致估计结果不一致或检验结果无效。当横截面个体数量N较少、时间序列维度T比较长时，可以构建似不相关回归(Seemingly unrelated regression,SUR)模型，并采用广义最小二乘估计法进行参数估计。但是当时间维度不够长，或者当N＞T时，SUR模型就不可行了，对于N＞T的情形目前主要有空间相关和残差共同因子结构两种处理方式[7]。本文主要考虑因子结构的情形。

1.1 存在性检验

为了检验截面个体之间是否存在相关性，早期较为常见的方法是Breush和Pagan(1980)提出的基于LM的截面相关存在性检验，检验的原假设为对于所有的t，当i≠j时，有cov(uit'ujt)=0。统计量为：

其 中为原模型OLS回归的残差。但是，统计量CDlm在N＞T的情况下表现欠佳，所以，Pesaran(2004)[8]提出了另一个修正的检验统计量：

并论证了该统计量在结构变化和异质动态面板数据模型中检验的稳健性。韩本三等(2011)[9]、Pesaran等(2008)[10]均对CD统计量进行了再修正研究，分别提出了NLM和MCD检验统计量。

1.2 强弱相关

截面个体之间的相关是以怎样的形式或者程度存在的，还需要进一步研究。截面相关面板数据的因子结构可以分为截面弱相关(cross-sectionally weakly dependent,CWD)和截面强相关(cross-sectionally strongly dependent,CSD)。对于给定的时间点t∈Γ，满足条件=0,则称序列{zit}为截面弱相关；若满足条件≥K＞0,则称序列{zit}为截面强相关。其中，Γt-1为信息集为加权平均值且wt和zt满足两个假设条件，具体信息可以参见文献[7]。在实际应用过程中，需要考虑不同的信息集，对于动态数据模型，信息集应该包含所有的滞后变量，比如在平稳面板数据模型中，信息集可以是截面个体的无条件协方差均值。

对于共同因子模型：

其中，共同因子 fjt为零均值方差为1的协方差平稳过程。条件方差为在多因子模型中，如果则因子 fjt为强因子；若K＜∞，则因子 fjt为弱因子。Chudik等(2011)[7]中还对半强或半弱的因子进行了定义。

1.3 因子处理

在处理截面相关时，Coakley等(2002，CFS)提出了用OLS残差的主成分来进行扩展回归，得到主成分估计量以处理截面相关。但是因为OLS估计时模型是存在截面相关的，且不可观测的因子与因变量之间可能还存在相关性，导致该估计量不满足一致性，所以建议用代理变量来进行截面相关的处理。Pesaran(2006)[11]考虑了两种不同但存在内在联系的方法来处理CFS统计量的不一致性，给出了具有一致性的CCE估计量(Common correlated effects estimators)，分别构建了基于组平均的CCEMG统计量和基于混合估计的CCEP统计量，用于处理面板回归模型中的多因子误差结构。Kapetaniosdeng等(2011)[12]将CCE方法扩展到非平稳共同因子结构。

Bai和Ng(2004)[13]将截面相关处理为共同因子结构，采用主成份方法进行退因子处理。因子模型为：

其中，eit为I(0)的误差序列，k为截面间共同因子的个数为因子载荷向量，Ft=(F1t'F2t'…'Fkt)′为共同因子。Bai和Ng(2002)[14]给出了确定k的取值k̂的检验标准，分别为PC和IC统计量：

PC(k)=V(k)+kg(N'T)'IC(k)=lnV(k)+kg(N'T)

共同因子和因子载荷可以通过最小化式（4）进行估计：

2 结构变化检验

面板数据结构变化点的检测，最早在Joseph和Wolfson(1992,1993)中有研究，他们建立了每个横截面序列都有突变点的随机突变模型(Random Breaks Model)，并假设所有突变点都是独立同分布的。面板数据结构变化的检验研究根据序列突变前后分布是否变化、突变序列的时间T是否固定（突变点是否会随总体时间长度而变化）、突变类型是均值突变还是方差突变、突变点是否内生等不同问题展开，这些问题与传统的时间序列结构变化研究比较类似。而面板数据结构变化比较独特的应用在于多个横截面个体的突变点是同质结构变化(homogeneous breaks)还是异质结构变化(heterogeneous breaks)。Bai和Carrion-i-Silvestre(2009)[15]中对面板异质结构变化进行了较广的定义，当不同截面个体具有不同的突变时间点，或者具有不同的突变程度，或者有不同数量的突变点，或者均值和方差突变发生在不同的时间点，都可以称为异质结构变化。本文以面板数据横截面个体结构变化时间点是否同期作为结构变化分类的唯一标准，其他情况在后续研究中再加以讨论。

2.1 同质结构变化

这里将面板数据同质结构变化理解为同期结构变化，即每个横截面个体的突变点时间是一致的。Bai(2010)[16]建立了面板数据共同突变点的估计方法，分别运用OLS和QML方法构建了均值和方差变化点的检验统计量，同时考虑了时间长度固定与变化两种情况，构建了面板数据模型共同突变点的一致估计量，并提出了用于研究其极限分布的新框架。鉴于Bai(2010)中检验方法简单且实用，下面着重介绍该方法。

均值变化模型为：

其中，i=1'2'...'N，μi1≠μi2，k0为未知结构变化点，eit为平稳过程，且E(eit)=0。为了估计均值结构变化点，构造了如下统计量：

其中为基于OLS方法的目标函数。一致性条件为

方差变化模型为：

其中，i=1'2'...'N ，μi1≠μi2，σi1≠σi2，k0为未知结构变化点，ηit为线性过程，且满足 E(ηit)=0 ，var(ηit)=1。为了估计方差结构变化点，构造了如下统计量：

其中为基于伪极大似然(quasi-maximum likelihood)方法的目标函数一致性条件为

2.2 异质结构变化

Joseph和Wolfson(1993)中较早地考虑了面板数据模型的异期随机突变点。面板数据异期结构变化点主要是将时间序列结构变化点的检验方法直接扩展到面板数据模型中，一般是直接采用时间序列结构变化点的估计方法去估计面板数据中各横截面个体的突变点。Costantini&Gutierrez(2007)[17]基于递归ADF检验统计量的联合概率构造异质非平稳面板数据模型的结构变化检验统计量；运用时间序列模型中参数估计的t统计量最大值构造结构变化点的检验统计量，并直接运用到面板数据模型中[18]；而文献[6,15]均采用了Bai和Perron(2003)[19]中提出的SSR统计量用于结构变化点的检验。

面板数据模型中检验异质结构变化点的SSR统计量构造如下：

其中为 基 于OLS方法的残差平方和，为第i个横截面个体的结构变化点。

3 交互效应分析

在非平稳面板数据模型构建过程中，已有诸多研究针对同时存在结构变化和截面相关情形的非平稳面板数据模型进行了研究[3,4,6,15]。在处理结构变化和截面相关时往往是将此两种情形分别进行检验和处理，均未考虑二者之间的交互影响效应。当假设面板数据截面独立时，单个个体结构变化不受其他截面变化的影响，此时与传统的单一时间序列结构变化类似，但是当面板数据存在截面相关时，每个截面个体的结构变化可能会因为其他截面的变化而发生改变。那么，截面相关的存在是否会改变横截面个体的结构变化？是否会引起结构变化点的发生时间？结构变化的存在是否会影响截面相关的因子结构？下面通过实证研究分析结构变化和截面相关之间的交互效应。

3.1 数据说明

外商直接投资与经济增长之间的影响关系历来受到研究者们的关注，面板数据模型是常用的分析工具之一。鉴于经济增长与外商直接投资关系研究的广泛性和实用性，本文采用中国30个省份(西藏除外)1995—2015年的国内生产总值GDP为被解释变量，外商直接投资FDI为解释变量，分析其基本结构和交互影响关系。考虑到物价和计量单位的影响，在计算时采用变量的对数形式。

首先采用Pesaran(2004)[8]提出的截面相关CD检验统计量进行相关结构判断。考虑的模型形式为：

原假设为不存在截面相关，检验统计量CD=81.9235，概率 p-value=0.00，检验结果说明模型存在截面相关。

再采用Pesaran(2007)[20]中提出的适宜截面相关的面板单位根检验方法，原假设为存在单位根，检验形式为带趋势项和常数项，检验结果为CIPSlog(GDP)=-0.49，CIPSlog(FDI)=-1.43，当显著性水平选定为0.05时log(GDP)和log(FDI)均存在单位根，属于非平稳面板数据。

3.2 模型设定与假设

借鉴文献[3,4,6]中非平稳面板数据模型形式，设：

其中，xit和 yit分别为解释变量和被解释变量，μi为个体常数项，Ft为共同因子，λi为因子权重值。表示均值结构变化表示方差结构变化，Dit=θiDUk+σiDTk表示结构变化函数。

00

为了分析共同因子与结构变化之间的交互效应影响，假设原假设为 H0:θi=0'σi=0 。备择假设为 H1:θi≠0或σi≠0。模型调整为:

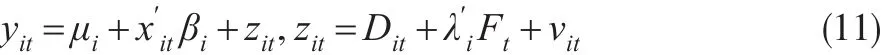
若原假设不成立，说明回归残差zit存在均值或方差结构变化，反之，若不存在均值或方差结构变化，说明原假设成立。

在原假设成立的情况下，首先采用Bai和Ng(2004)[13]中的方法计算共同因子，并对去掉因子影响的残差vit进行截面相关检验，检验统计量CD=-1.8964，概率 p-value=0.971，表明已不存在截面相关，这说明模型中Ft项是存在的。

3.3 结构变化检验

采用Bai和Perron(2003)[19]和Bai(2010)[16]中提出的方法检验结构变化，并对去共同因子的序列和带共同因子的序列分别进行检验以说明共同因子对结构变化的影响，其中T=21 ，N=30 ，k0=floor[τ×T] ，τ∈[0.1'0.15,…,0.85,0.9]，有17个结构变点。图1为原始数据log(GDP)和log(FDI)的分析图，SSR取值满足一致性条件且有最小值，说明二者均存在均值和方差结构变化。图中纵坐标为统计量SSR的值，横坐标为结构变化点的序号。 floor[·]为R程序里的一个取值函数。

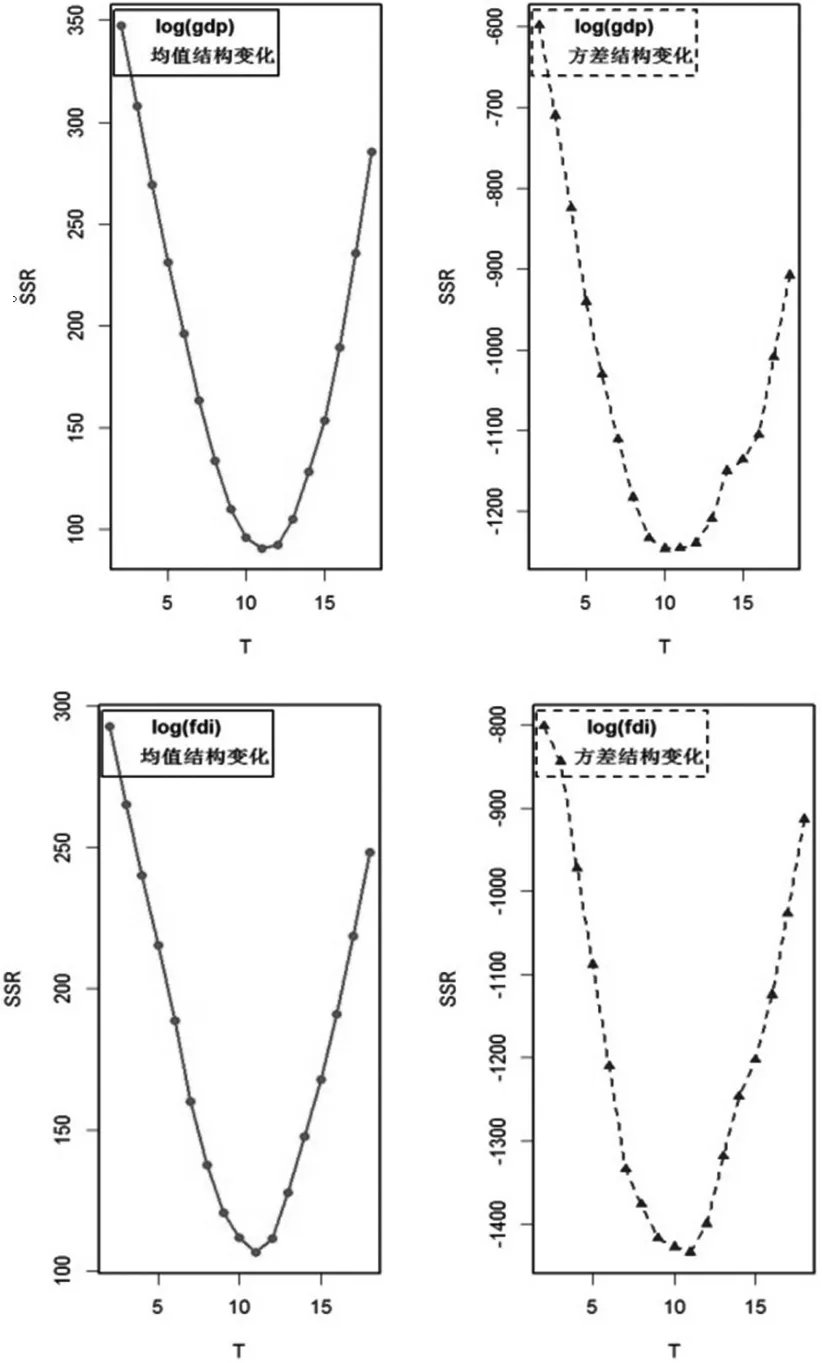
图1 log(GDP)与log(FDI)数据结构变化检验图

在原假设成立的情况下，图2为按照调整模型(11)计算而得的残差序列结构变化检验图，结果显示残差zit存在均值和方差结构变化点，即其数据生成方式为zit=Dit+但是图2右边去掉共同因子以后残差序列结构变化检验图

显示，均值结构变化的SSR取值范围为4.93×10-29～5.49×10-29，方差结构变化的SSR取值范围为-43350～-43182，不满足结构变化一致性条件，不存在均值和方差结构变化，说明有均值和方差结构变化，其去掉共同因子后没有结构变化，前后检验结果发生了矛盾，这说明模型结构的设定出现了问题，模型形式与数据结构不符合，有可能是共同因子的存在改变了截面个体的结构变化状态，这正是本文质疑且尚待检验的问题。

图2 残差序列结构变化检验图

3.4 交互效应

进一步地，借鉴式(9)的检验公式对共同因子结构进行结构变化检验，结果见下页图3。因子权重λi是横截面数据，样本量为N=30，其数据结构变化体现为地域异质性，这里不作考虑。尽管如此，图3中仍然给出了因子权重序列的SSR值，图形显示存在多个极小值，这说明所选30个省市权重值差异较大，存在多种类型。对于共同因子序列Ft，当k0=18，即2012年时均值结构检验的SSR值达到最小，说明共同因子Ft存在均值结构变化，同时，在k0=8，即2002年时均值结构检验的SSR值有极小值，这与方差结构检验一致。由此，可以认为共同因子序列Ft存在均值和方差结构变化。这说明模型(10)中的结构变化并不是独立存在的结构变化，而是由共同因子结构变化体现出来。这表明截面相关与结构变化之间的交互效应确实存在，而且正影响着非平稳面板数据传统建模基本范式的使用。

图3 因子结构变化检验图

3.5 实证分析

表1给出了结构变化具体时点。经过实证分析得出了有别于常规应用模型设定的结论:首先，中国区域GDP增长率在2004—2005年发生了较为明显的结构变化，这源于1995—2005年、2006—2015年两个时间段内区域经济增长模式、经济结构均发生了较大的改变。区域FDI增长率在2005年发生了较为突出的结构变化，这与2005年中国汇率制度改革、外贸政策调整是分不开的。模型回归残差分别在2008年和2004年表现出均值和方差结构变化，说明对GDP增长率产生影响的其他因素在这期间也有不同程度的结构改变。

表1 结构变化时点说明

其次，影响GDP和FDI结构变化的主要来源是2002年的共同因子，与其他误差项关系不显著。2002年是我国加入WTO的第一年，各省市面临的对外贸易国际环境发生了巨大改变，全国采取了一系列有效举措促进国际贸易全面发展，以拉动国民经济快速增长。这些来自全国的经济结构调整和战略部署形成了影响30个省市的共同因子，而权重系数的区间异质则表明不同省市之间的实施力度是有差异的。

最后，对中国30个省份1995—2015年的国内生产总值GDP和外商直接投资FDI建立如前设计的模型是不恰当的。在研究国内生产总值与外商直接投资的协同关系时，若以回归残差的结构变化作为协同关系的结构变化是有误的，因为二者协同关系的结构变化主要来源于共同驱动因素，而不是其他误差因素。因此，更适宜的模型形式应当为：

4 结论

截面相关的非平稳面板数据建模一般优先考虑建立带共同因子的面板协整模型，模型形式的设定关系着检验结果的准确性，因此数据结构内在逻辑至关重要。本文发现已有文献中对截面相关和结构变化采取分别处理的方式进行建模研究，忽视了二者之间的交互效应，进而对非平稳面板数据建模基本范式的使用过程提出质疑，认为面板数据基本结构分析是所有模型构建和参数估计的根本，不适宜的模型搭建将给出不恰当的分析结论。

本文采用实际经济数据进行分析，得出非平稳面板数据模型中共同因子和结构变化的交互效应确实存在的结论，这说明对基本范式的部分质疑成立。结果显示在非平稳面板数据模型中要区分结构变化的来源因素，特别是由共同因子结构带来的结构变化，否则将导致模型中传统结构变化处理方法失效。所以，在实证模型构筑之前应当进行数据基本结构检验，以最适宜的模型形式贴近数据真实生成过程。

[1]陈海燕.面板数据模型的检验方法[M].北京：经济科学出版社,2012.

[2]Baltagi B H,Song S H,Kwon J H.Testing for Heteroskedasticity and Spatial Correlation in a Random Effects Panel Data Model[J].Computational Statistics&Data Analysis,2009,53(8).

[3]Banerjee A,Carrion-i-Silvestre J L.Cointegration in Panel Data With Breaks and Cross-section Dependence[J].Journal of Applied Econometrics,2015,30(1).

[4]Westerlund J,Edgerton D L.A Simple Test for Cointegration in Dependent Panels With Structural Breaks[J].Oxford Bulletin of Economics and Statistics,2008,5(70).

[5]珂英,张鸿武.城镇化与工业化对能源强度影响的实证研究——基于截面相关和异质性回归系数的非平衡面板数据模型[J].中国人口·资源与环境,2016,26(6).

[6]王维国,薛景,于刚.基于结构突变和截面相关的面板协整检验[J].数量经济技术经济研究,2013,(5).

[7]Chudik A,Pesaran M H,Tosetti E.Weak and Strong Cross-section Dependence and Estimation of Large Panels[J].Econometrics Journal,2011,(14).

[8]Pesaran M H.General Diagnostic Test for Cross Section Dependence in Panels[J].University of Cambridge＆USC,2004.

[9]韩本三,徐凤,黎实.面板数据模型的截面相关检验研究[J].统计研究,2011,28(12).

[10]Pesaran M H，Ullah A,Yamagata T.A Bias-Adjusted LM Test of Error Cross Section Independence[J].Econometrics Journal,2008，(11).

[11]Pesaran M H.Estimation and Inference in Large Heterogeneous Panels With a Multifactor Error Structure[J].Econometrica,2006,74(4).

[12]Kapetanios G,M H Pesaran,T Yagamata.Panels with non-stationary Multifactor Error Structures[J].Journal of Econometrics,2011,160.

[13]Bai J,Ng S.A Panic Attack on Unit Roots and Cointegration[J].Econometrica,2004,72(4).

[14]Bai J,Ng S.Determining the Number of Factors in Approximate Factor Models[J].Econometrica,2002,70.

[15]Bai J,Carrion-i-Silvestre J L.Structural Changes,Common Stochastic Trends,and Unit Roots in Panle Data[J].The Review of Economic Studies,2009,(76).

[16]Bai J.Common Breaks in Means and Variance for Panel Data[J].Journal of Econometrics,2010,157(1).

[17]Costantini M,Gutierrez L.Simple Panel Unit Root Tests to Detect Changes in Persistence[J].Economics Letter,2007,(96).

[18]Kapetanios G.Unit Root Testing Against the Alternative Hypothesis of up to M Structural Breaks[J].Journal of Time Series Analysis,2005,(26).

[19]Bai J,Perron P.Computation and Analysis of Multiple Structural Change Models[J].Journal of Applied Econometrics,2003,18(1).

[20]Pesaran M H.A Simple Panel Unit Root Test in the Presence of Cross-section Dependence[J].Journal of AppliedEconometrics,2007,22(2).