基于VAR-VEC组合模型的CCI与PPI关系研究

罗耀宁，唐国强，缪巧芬

（桂林理工大学 理学院，广西 桂林 541004）

0 引言

消费者信心指数（CCI）和生产价格指数（PPI）都是衡量我国经济发展趋势的重要宏观经济指标。消费者信心指数（CCI）是反映消费者信心强弱的指标，是综合反映并量化消费者对当前经济发展形势评价和对经济前景、收入水平、收入预期以及消费心理状况的主观性感受，是预测经济未来走势和消费未来趋向的一个先行指标，是监测经济周期是否发生变化的重要依据。生产价格指数（PPI）是衡量工业企业产品出厂价格变动趋势和变动情况的指标，是反映某一时期生产领域价格变动状况的重要经济指数，也是制定有关经济政策和国民经济核算必不可缺的依据。与居民消费价格指数（CPI）不同，生产价格指数（PPI）主要的目的是衡量企业购买的一篮子物品和劳务的总费用。因为企业最终会把总费用以更高的消费价格转移给消费者，所以，通常认为生产价格指数的变动来预测消费物价指数的变动是有意义的。

不少学者对CCI和PPI的模型和预测进行研究，张晓帅等（2012）[1]运用改进灰色模型对我国CCI进行预测；徐婷（2013）[2]利用时间序列模型方法对我国CCI建立了组合预测模型；董大勇等（2016）[3]应用ARIMA模型对PPI进行建模，并做出了短期的预测；赵永兴等（2013）[4]用PPI月度数据来构建EGARCH（1，1）模型，说明了PPI存在ARCH效应。还有很多文献分别研究CCI、PPI与其他经济指标之间的关系。何毅等（2012）[5]探讨了CCI对CPI的影响效应；李跃辉等（2012）[6]指出CPI、CCI和PMI（采购经理人指数）之间存在长期稳定的协整关系；何跃等（2016）[7]探讨PPI对GDP的预警作用，从而为宏观经济政策提供依据。以上文献研究表明了CCI和PPI分别与CPI存在一定关系，并且两者都是反映经济发展趋势的重要指数。本文通过拟合VAR-VEC组合模型探讨CCI与PPI之间是否存在关系。

1 理论与建模步骤

1.1 VAR模型

向量自回归模型（VAR模型）在1980年由西姆斯（Sims C A）提出，主要应用于分析和预测随机扰动对系统的动态冲击，冲击的大小、正负及持续的时间[8]。VAR模型是在数据的统计性质基础上建立模型，它把系统中每一个内生变量作为系统中所有内生变量的滞后阶数来构建模型，从而将单变量自回归模型推广到多元时间序列变量组成的向量自回归模型中去。

设 Yt=(y1t，y2t，…，ynt)′是 n×1阶的时间序列向量，p阶VAR模型（记为VAR（p））的表达式为：

其中，p是最大滞后阶数，∏i(是第i个待估参数n×n阶矩阵，μt是n×1阶随机误差列向量，∑是n×n阶协方差矩阵。

VAR(p)模型的稳定条件是要求特征方程的根都落在单位圆以内。

1.2 Johansen协整检验[9]

1990年Johansen与Juselius一起提出了Johansen协整检验，它是基于VAR模型检验回归系数的一种检验方法，也可以用于多变量之间的协整检验。

对于n个时间序列Yt=(y1t，y2t，…，ynt)T，可以利用协整定义讨论这n个变量之间是否存在协整关系。协整的定义如下：

n维向量时间序列Yt的分量间d'b阶协整，记为Yt～CI(d'b)，如果满足：

（1）Yt～I(d)，要求Yt的每一个分量都是d阶单整的；（2）存在非零向量 β ，使得 β′Yt～Ι(d-b)，0＜b≤d 。简称yt是存在协整关系的，向量β为协整向量。对于n维向量时间序列Yt至多存在n-1个线性无关的协整向量。

1.3 脉冲响应函数的基本思想[10]

本文以含有两个变量的VAR（2）模型为例，介绍脉冲响应函数分析方法的基本思想。

式（2）中是待估参数，随机扰动项μt=(μ1t'μ2t)′，假设是具有以下性质的白噪声向量：

Ε(μit)=0，对于∀t，i=1'2

var(μt)=Ε(μtμt′)=∑，对于∀t

Ε(μitμis)=0，对于∀t≠s，i=1'2

假设是从第0期开始活动，且设 y1t-1=y1t-2=y2t-1=y2t-2=0，又设在第0期给定了扰动项 μ10=1，μ20=0，且其他扰动项均为0，即 μ1t=μ2t=0(t = 1，2，…) ，称此为第0期对 y1t的脉冲响应。同样地，当扰动项μ10=0，μ20=1，且其他扰动项均为0，即 μ1t=μ20=0(t = 1，2，…) ，称此为第0期对y2t的脉冲响应。

1.4 VEC模型[10]

Engle和Granger将协整理论与误差修正模型结合起来，建立了向量误差修正模型，即VEC模型。只要变量之间存在着协整关系，就可以由自回归分布滞后模型导出误差修正模型（ECM）。而在VAR模型中每一个方程都是一个自回归分布滞后模型，因此，可以认为VEC模型是含有协整约束的VAR模型。

根据协整方程可得到VEC模型的表达式：

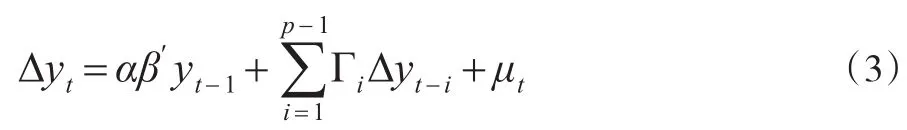
其中是 yt经过差分变换的平稳值，α为系数向量，β为协整向量，μt为随机扰动向量。

式（3）也可以表示为：

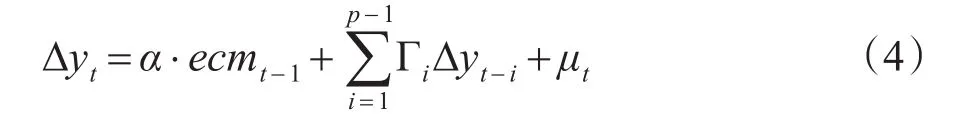
式（4）中的每一个方程都是一个误差修正模型。其中ecmt-1=β′yt-1是误差修正项向量，反映变量之间的长期均衡关系。系数向量α反映了变量之间偏离长期均衡状态时，将其调整到均衡状态的调整速度。所有作为解释变量的差分项的系数反映各变量的短期波动对作为被解释变量的短期变化的影响。

1.5 基于VAR-VEC组合模型的建模步骤

本文通过建立一个VAR-VEC组合模型，运用协整检验、脉冲响应函数等分析方法探究CCI与PPI的关系。建模步骤如下：

（1）为消除季节趋势和异方差性、减少波动，分别对CCI序列、PPI序列取对数，记为LNCCI序列和LNPPI序列；

（2）对CCI、PPI、LNCCI、LNPPI序列进行平稳性检验，并对非平稳序列做平稳处理；

（3）根据AIC准则和SC准则确定VAR模型的最大滞后阶数p；

（4）以最大滞后阶数p构建VAR（p）模型，并利用AR根的图表验证VAR（p）模型的稳定性；

（5）对一阶单整序列LNCCI和LNPPI做Johansen协整检验，检验两者之间是否存在长期协整关系；

（6）在协整检验的基础上，做VAR模型的脉冲响应函数并进行相应分析；

（7）基于VAR模型引入VEC模型探究变量之间的短期波动和长期均衡。

2 实证

2.1 数据来源

本文数据来源于东方财富网（http://data.eastmoney.com/cjsj/），选取2010年1月至2016年9月的我国消费者信心指数（CCI）和生产价格指数（PPI）月度数据，共有81个时间点，图1为我国消费者信心指数（CCI）和生产价格指数（PPI）的时间序列图。

图1 CCI与PPI的时间序列图

2.2 序列的平稳性检验

从图1可以看出，CCI序列和PPI序列随着时间变化而有所变化，从直观上判断可知CCI序列和PPI序列具有明显的非平稳性。需要对序列进行单位根检验以判断其平稳性。为消除季节趋势和异方差性、减少波动，对序列CCI、序列PPI分别取对数，记为序列LNCCI和序列LNPPI。再对两组对数序列进行一阶差分，生成的序列分别记为序列DLNCCI和DLNPPI，并对两序列进行单位根检验。

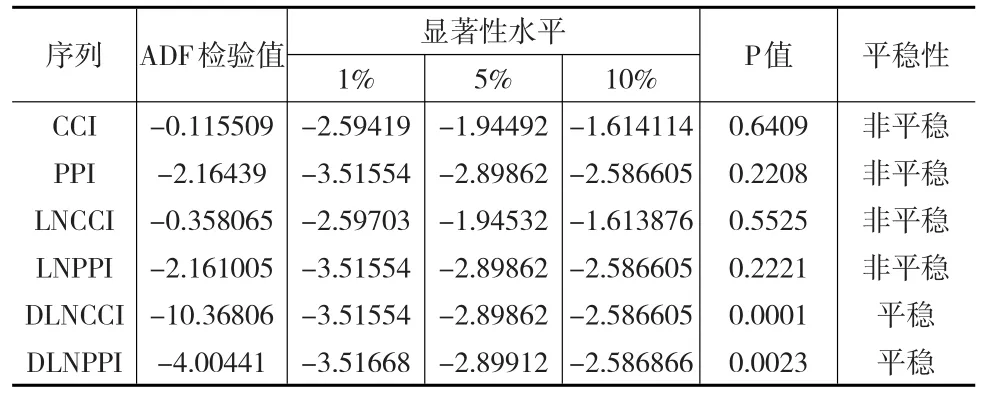
表1 两序列的单位根检验结果

由表1可知，原始序列CCI、PPI、LNCCI和LNPPI的ADF检验值均大于检验水平为1%、5%和10%的t统计量临界值，同时概率P值均大于0.05，因此不拒绝原假设，即认为原始序列CCI、PPI、LNCCI和LNPPI是非平稳序列。经过差分后的序列DLNCCI和DLNPPI，ADF检验值均小于t统计量临界值，同时概率P值均小于0.05，因此，可以认为序列DLNCCI和DLNPPI为平稳序列。序列LNCCI和LNPPI都是一阶单整序列，说明两者之间可能存在着长期的协整关系。

2.3 VAR模型最大滞后阶数的确定

在构建VAR模型之前，可以依据赤池信息准则（AIC）和施瓦茨（SC）准则来确定模型的最大滞后阶数p，结果如表2所示。

表2 最大滞后阶数选择准则

从表2可看出，AIC和SC最小值对应的阶数p均为2，故VAR模型选择滞后阶数p=2为最大滞后阶数。

2.4 VAR模型的建立和检验

根据前面的已知条件，所建立的VAR（2）模型可写成矩阵形式（5）：

VAR（2）模型的AIC值为-12.56607，SC值为-12.26614，AIC和SC值都很小，说明所建立的VAR（2）模型效果较好。为了检验VAR模型的平稳性，本文选择使用AR根的图表验证。从图2可以很直观地看出，所有单位根的倒数的模都落在了单位圆之内，因此，所建立的VAR（2）模型是稳定的。

2.5 Johansen协整检验

序列为非平稳序列时，构建模型很可能出现伪回归。协整检验的目的就是检验回归方程所描述的因果关系是否是伪回归，即检验变量之间是否存在长期稳定的关系。协整检验要求各序列是非平稳序列，并且是同阶单整序列。从单位根检验结果可以知道，序列LNCCI和LNPPI满足协整检验的要求。

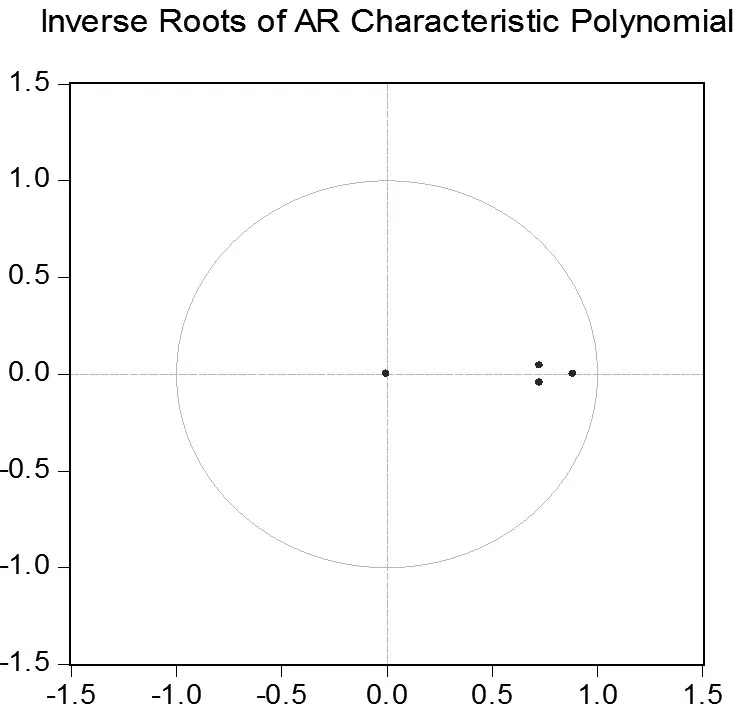
图2 AR单位根的分布图

表3 Johansen协整检验结果

从表3可知，在5%的置信水平下，特征值和迹统计量检验值均大于临界值，第一行、第二行P值分别为0.0198和0.0351，均小于0.05，拒绝了不存在协整关系的原假设，即说明消费者信心指数与生产价格指数之间存在长期协整关系。经过标准化协整系数后，所得到的协整方程如下式（6）所示：

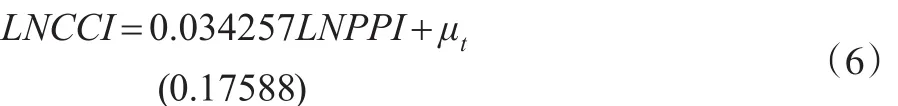
2.6 脉冲响应函数分析

为了描述在随机误差项上施加一个标准差大小的冲击对变量的当前值和未来值所产生的影响大小，本文采用脉冲响应函数分析我国消费者信心指数与生产价格指数的响应情况。

图3 脉冲响应函数合成图

由图3的脉冲响应结果可知，我国消费者信心指数对自身的冲击响应，第1期达到了最大值0.023575，随后开始下降直到趋向于0，由此可见，我国消费者信心指数对自身存在着短期的干扰，但是从长远来看，消费者信心指数对自身的影响作用很小，几乎不受自身影响。我国消费者信心指数对生产价格指数第1期没有立即做出反应，随着滞后期的延长开始上升，第4期上升到最高点0.002356后逐渐下降近趋向于0，因此，无论从长期还是短期来看，虽然消费者信心指数对生产价格指数会产生一定的冲击，但是影响作用不大。

生产价格指数第1期开始就对自身的冲击响应，第6期达到最大值0.011073，随后开始下降但不为0，说明生产价格指数对自身有着一定的长期影响。生产价格指数对我国消费者信心指数有着一定的影响，前3期对消费者信心指数产生冲击力很小的正向作用，但是到第4期开始做出负向反应，并且长期趋向于-0.002，因此，虽然生产价格指数对我国消费者信心指数没有立即做出响应，开始呈现正向影响，但是从长期趋势来看，生产价格指数对我国消费者信心指数有着长期的负向影响。当生产价格指数增加时，消费者对经济走势信心会有所下降。

2.7 VEC模型建立和参数估计

由Johansen协整检验可知，消费者信心指数与生产价格指数之间存在着长期的协整关系。基于前面的VAR（2）模型可以建立VEC模型分析两者之间的长期稳定关系以及短期波动情况。

VEC模型：

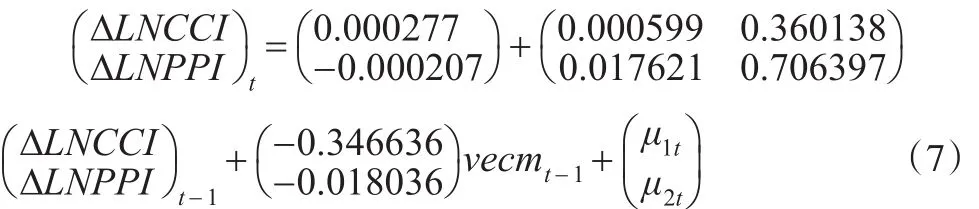
其中，协整方程vecmt-1：

从VEC模型的估计结果可知，模型中的AIC值为-12.5099，SC值为-12.20997，两个值都较小，说明VEC模型是非常合理的。从式（7）可以看出，前一期的CCI和PPI对本期的CCI有着正向作用，且PPIt-1影响最大，说明上一期的生产价格指数上涨，会增强本期的消费者信心指数。在长期均衡关系中，CCI和PPI每增加一个百分点，下一期的CCI分别增加0.000599、0.360138个百分点。VECM是误差修正项，其系数是负值，说明CCI以0.346636的值反向修正下一期的CCI值以到达一个长期均衡的状态。生产价格指数适当增大有利于提高消费者信心指数，有利于促进社会经济稳定发展。

图4是变量CCI和PPI之间的协整关系曲线，从整体上看，从2010年到2013年底和2015年，尤其是2011年底和2013年，误差修正项的绝对值偏离较大，也就是说短期波动偏离了长期均衡。2014年开始，误差修正项的波动幅度开始变小，逐渐回到长期均衡的状态。

3 结论

本文运用VAR-VEC组合模型对我国消费者信心指数和生产价格指数进行实证分析，研究了CCI和PPI之间的协整关系，得到以下结论：

图4 LNCCI和LNPPI的协整关系图

（1）LNCCI序列和LNPPI序列经过一阶差分后达到平稳，都属于一阶单整序列。利用两序列滞后2期高度显著，构建VAR（2）模型，说明了当期的消费者信心指数和生产价格指数会受到前2期的变化影响。

（2）LNCCI和LNPPI之间存在协整关系，表明消费者信心指数与生产价格指数之间存在长期稳定的关系。

（3）LNCCI和LNPPI的脉冲响应情况表明CCI对自身有短期波动的影响，几乎不存在长期影响；无论是从短期波动，还是长期影响来看，CCI对PPI都产生一定的冲击影响，但是冲击力度不大。PPI对自身存在一定的影响，对CCI存在长期负向影响。

（4）VEC模型分析了CCI和PPI之间的长期稳定关系以及短期波动情况，当期的CCI、PPI都会受到前一期的CCI和PPI正向影响。误差修正项系数是负值，起到反向修正下一期CCI、PPI值以达到长期均衡状态的作用。

[1]张晓帅，姚俭.运用改进灰色模型预测消费者信心指数[J].统计与决策，2012，（19）.

[2]徐婷.时间序列模型在消费者信心指数预测中的应用[D].大连：辽宁师范大学学位论文，2013.

[3]董大勇，刘珂言.基于ARIMA模型的工业品出厂价格指数预测与分析[J].统计与决策，2016，（1）.

[4]赵永兴，孙高洁.基于EGARCH模型的我国工业品出厂价格指数（PPI）波动的实证研究[J].市场经济与价格，2013，（3）.

[5]何毅，王新.消费者信心指数对CPI的影响效应探讨[J].价格理论与实践，2012，（12）.

[6]李跃辉，彭嘉莹.基于VAR-VEC模型的物价指数关系研究[J].统计与决策，2012，（15）.

[7]何跃，侯婧.生产价格指数对宏观经济预警与实证[J].统计与决策，2016，（20）.

[8]Sims C A.Macroeconomics and Reality[J].Econometrica，1980，(48).

[9]Johansen S，Juselius K.Maximum Likelihood Estimation and Inferences on Cointegration-with Applications to the Demand for Money[J].Oxford Bulletin of Economics and Statistics，1990，(52).

[10]高铁梅.计量经济分析方法与建模——EViews应用及实例[M].北京：清华大学出版社，2009.