一道课后练习题的多视角解析

费 明

(江苏省江阴市第一中学 214400)

学生在学习二项式定理后，在配套习题中遇到这么一个题目：

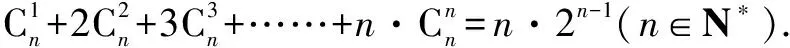
下面笔者给出几种证明方法供大家参考.

方法一：考察函数f(x)=(1+x)n(n∈N*).

两边求导：

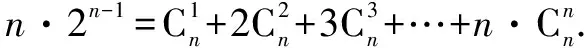
不妨把这种方法称为“求导法”.

方法二：令

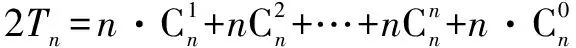
∴Tn=n·2n-1,

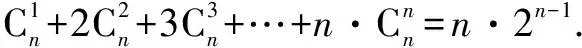
不妨把这种方法称为“倒序相加法”.

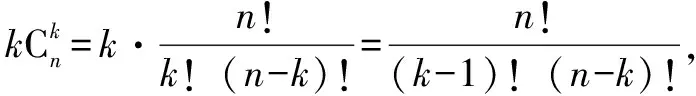
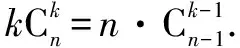
=n·2n-1.

这种方法是利用了组合数的性质来证明的.

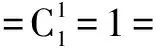
(2)假设当n=k时，结论正确.

则当n=k+1时,

=k·2k-1+2k+k·2k-1=k·2k+2k=(k+1)·2k,

∴当n=k+1时结论正确.

……

T=T1+T2+…+Tn

T=2n·n-T,

T=n·2n-1.

不妨称这种方法为分组累加法.

甚至我们还有通过这样的问题情景来说明这个等式的正确性：某校高二(3)班一共有n个学生，现在要在这n个学生中组建一个学习小组(人数大于等于1人)，并任命一个组长.

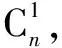
另一方面：学习小组的人数可以1个，2个，…，n个.

…

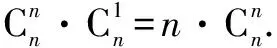
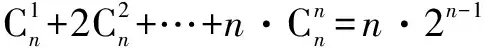
参考文献：

[1]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心. 普通高中课程标准实验教科书(数学选修2-2)[M].北京:人民教育出版社,2008.