由高考题引起的教学思考

于东威

(山东省东营市胜利第一中学 257000)

曲线的曲率半径本是高等数学中一个问题，在大学物理力学和全国中学生物理竞赛中也有要求，在高中物理教学过程中，则不做要求.然而最近几年的高考试题中出现了与曲线的曲率半径相关的问题，在平时的教学中并不要求掌握这些概念，给学生的理解造成了一定的困难.

一、高考试题分析

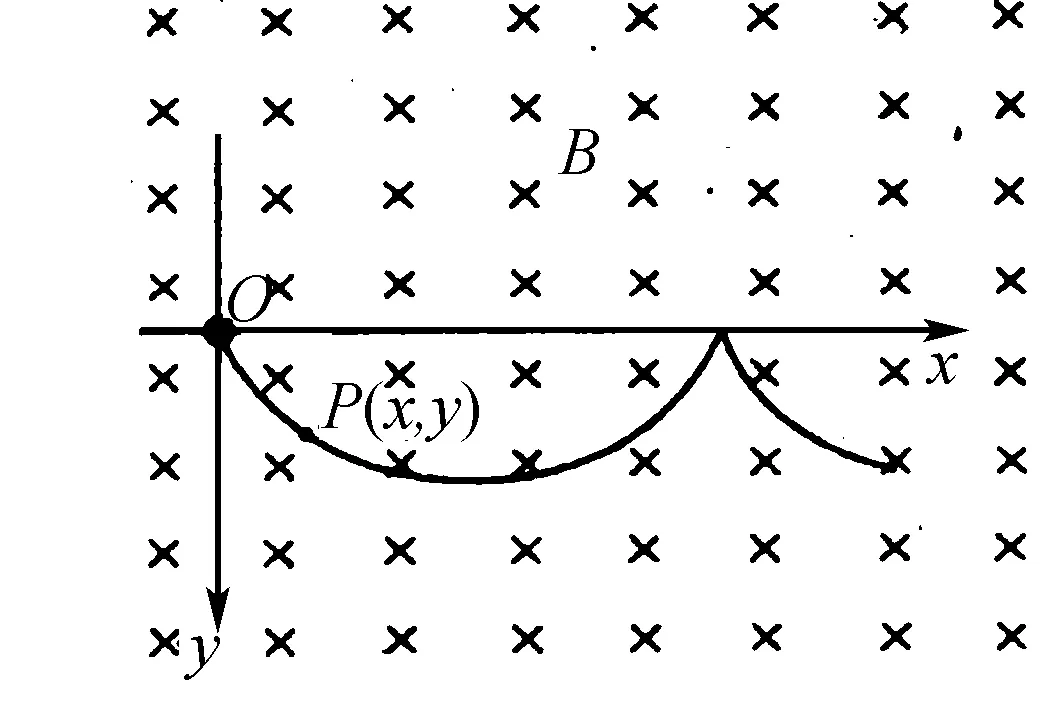
图1

我们首先来看2008年江苏高考理综第14题：在场强为B的水平匀强磁场中，一质量为m、带正电q的小球在O静止放，小球的运动曲线如图1所示．已知此曲线在最低点的曲率半径为该点到z轴距离的2倍，重力加速度为g．求：

(1)小球运动到任意位置P(x，y)的速率v.

(2)小球在运动过程中第一次下降的最大距离ym.

解析(1)洛伦兹力不做功，由动能定理得：

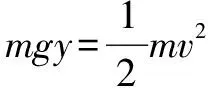
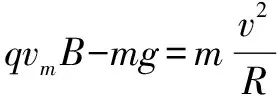
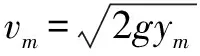
另由题目条件可知：R=2ym⑤

本题对于竞赛学生而言，有三种解题方式，微元法、平均值法和速度分解法，但这三种方法对于没有学过竞赛的普通高考学生而言，难度是很大的，虽然为了降低难度，在本题中增设了曲率半径这个条件，但教师如果在平时的课堂教学中对曲率半径的知识点没有必要的补充，学生一时很难理解，务必会对解题带来一定的困难.

再来让我们看看2011年安徽高考理综第17题.如图2(a)所示，曲线上的A点的曲率圆定义为：通过A点和曲线上紧邻A点两侧的两点作一圆，在极限情况下，这个圆就叫做A点的曲率圆，其半径ρ叫做A点的曲率半径.现将一物体沿与水平面成α角的方向已速度υ0抛出，如图2(b)所示.则在其轨迹最高点P处的曲率半径是( ).

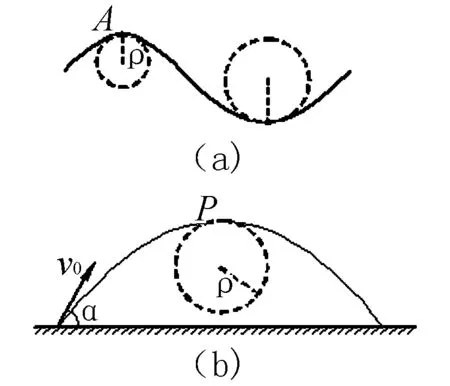
图2

本题也是关于曲率半径的问题，同样为了降低难度，在题干中先讲解了曲率半径的定义，然后给出斜抛的模型，让学生求解最高点的曲率半径.

二、问题分析与解决

对于曲率半径的问题，人教版高中物理必修二第五章第六节中有涉及，教材设置这一部分的目的，是要学生在更一般，更广阔的背景下认识圆周运动和曲线运动，目的主要是让学生开阔视野，所以在高中物理教学中分析一般情况下的变速圆周运动的问题时，尽管提到切向分力和法向分力，但并不要求学生掌握这些概念，教学中也没有进行定量研究.

类似的问题在高中物理教学中还有很多，比如参照系的选择问题.高中物理教材将物体相对于地面的运动称为对地运动简称为运动，将相对于其他物体的运动称为相对运动，在平时的课堂教学中无论教师还是学生都已习惯选择地面为参照系而忽视了相对运动，没有意识到恰当的选择其他物体为参照系，可以使问题得到极大的简化，从而起到事半功倍的效果.

在平时的课堂教学中，除了吃透考试大纲之外，还应该吃透教材，并深挖教材中比较模糊的知识点，这样才能让学生的知识体系更系统，从而提高分析问题解决问题的能力.

参考文献：

[1]张大昌.普通高中课程标准实验教科书物理(必修2)[M].北京:人民教育出版社,2006.