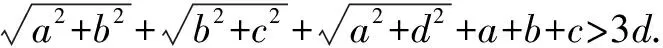培养“以形助数”思想意识 开拓数学解题视野

许伟湘

(福建省漳州市诏安一中 363500)

一、利用数形结合的方法，巧用两点间的距离求最值问题

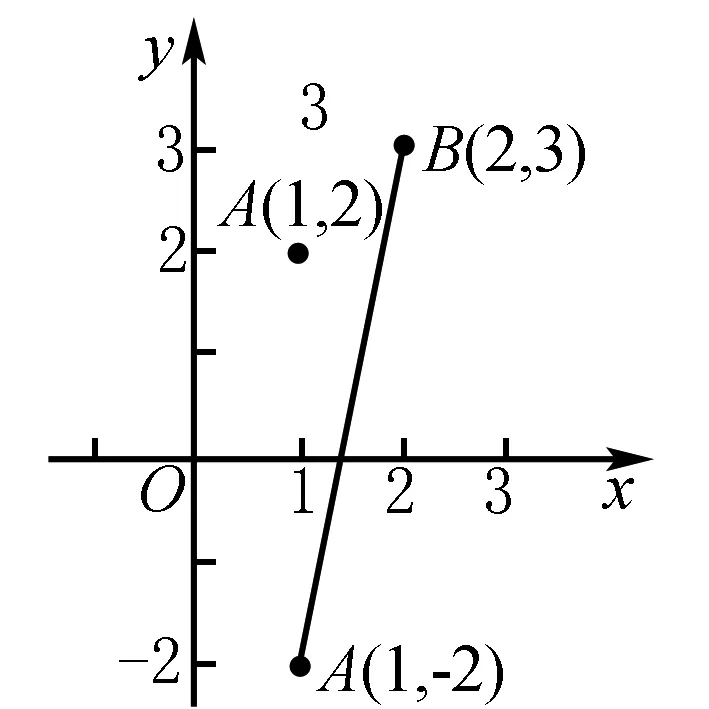
图1

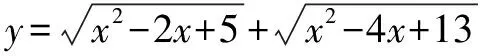
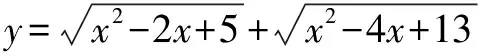
其几何意义是点P(x，0)到点A(1，-2)与点B(2，3)的距离之和的最小值.显然点P在AB上时y取最小值|AB|.

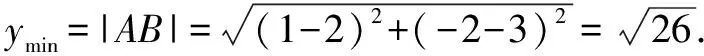
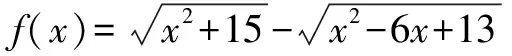
分析由于f(x)的解析式中含有两个根号，根号内部都是x的二次式，以中学的代数方法很难求出它的最大值，但如果巧妙用两点间的距离公式的方法，那么问题就简单了.

图2

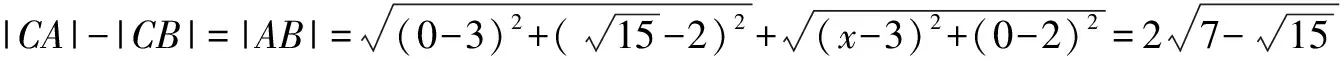
二、利用数形结合的方法，构成直线斜率问题解题

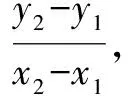
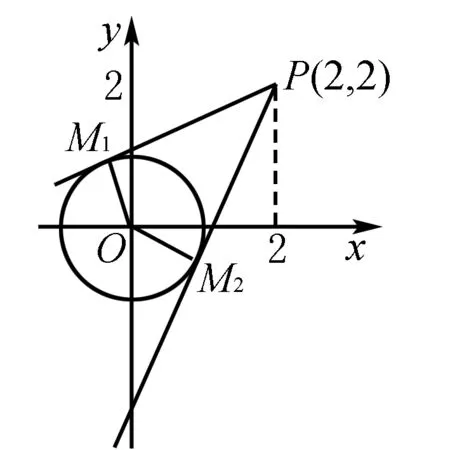
图3

分析单纯从代数角度考虑，当x使f(x)的解析式的分子取最大(小)值时，分母并不是最小(大)值，所以利用sinx和cosx的有界性，难以求得f(x)的最大(小)值，若A(cosx,sinx)，B(2，2)，f(x)就是AB的斜率，而A(cosx,sinx)在单位圆上，这样就很容易求解.

设经过点P(2，2)，斜率为k的直线l：y-2=k(x-2)与 圆x2+y2=1相切，切点为M1和M2.则函数最值转化为斜率的最值.

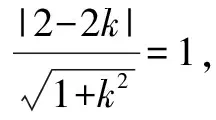
图4

设直线方程为y=kx.

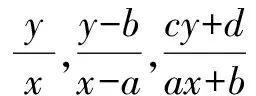
三、利用数形结合的方法，解决数列问题

利用数列的一些相关性质，往往可以把数列问题构造为一次函数来解题.

例5 设等比数列{an}的前n项和为Sn，若S3+S6=2S9，求公比q.

解根据题意知q≠1，由于点(q3,S3)、(q6,S6)、(q9,S9)共线，

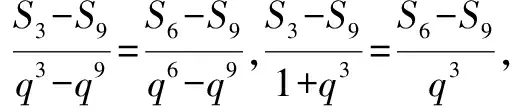
即q3(S3-S9)=(1+q3)(S6-S9) (*).

由已知S3-S9=2S9， ∴S3-S9=S9-S6，

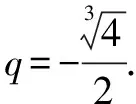
四、利用数形结合的方法，解决方程的根(函数的零点)的个数问题

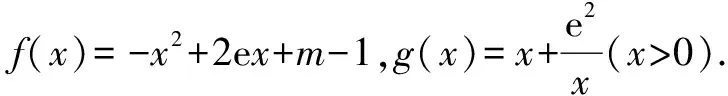
(1)若g(x)=m有零点,求m的取值范围;

(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.

分析：函数零点个数的判断方法:

(1)直接求零点:令f(x)=0,如果能求解,则有几个解就有几个零点;

(2)零点存在性定理:利用定理不仅要求函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)<0, 还必须结合函数的图象与性质(如单调性、奇偶性等)才能确定函数有多少个零点;

(3)利用图象交点的个数:画出两个函数的图象,看其交点的个数,有几个交点就有几个不同的零点.

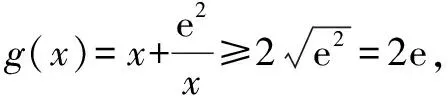
即m的取值范围为[2e,+∞).

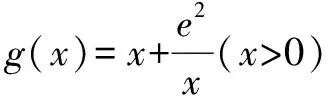
可知若使g(x)=m有零点,则只需m≥2e.

即m的取值范围为[2e,+∞).

(2)若g(x)-f(x)=0有两个相异的实根,

即g(x)与f(x)的图象有两个不同的交点,

∵f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2,

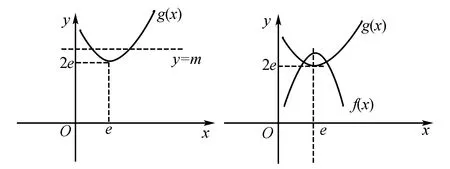
图5 图16

∴其图象的对称轴为x=e,开口向下,最大值为m-1+e2.

故当m-1+e2>2e,即m>-e2+2e+1时,g(x)与f(x)有两个交点,即g(x)-f(x)=0有两个相异实根.

∴m的取值范围是(-e2+2e+1,+∞).

五、利用数形结合的方法， 研究方程、曲线、函数、不等式中参数问题

诸多的关于方程或不等式的问题，往往可以转化为方程与不等式的函数图象关系来解决.

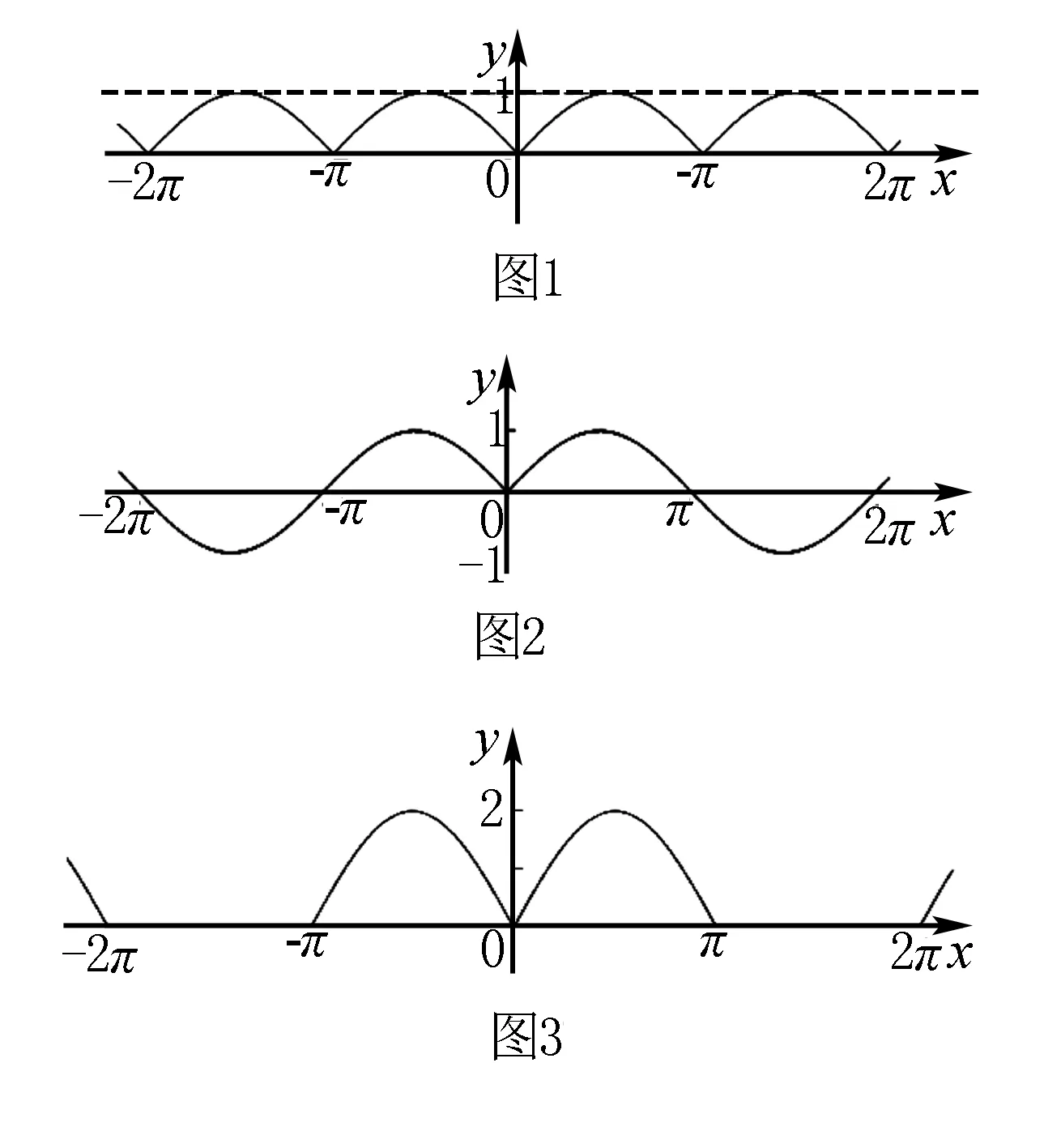
例7 设二次方程7x2-(a+13)x+a2-a-2=0的两根x1,x2满足0

图1

分析构造二次函数y=7x2-(a+13)x+a2-a-2，根据二次方程7x2-(a+13)x+a2-a-2=0的两根取值范围，来确定抛物线y=7x2-(a+13)x+a2-a-2与x轴的交点的横坐标的变化区域及纵坐标的情况.

解设y=7x2-(a+13)x+a2-a-2,作出此函数的大致图象(如图).

∵0

解此不等式组得：-2

例8 求函数y=|sinx|+sin|x|的最值.

解分别作出函数y=|sinx|(如图1)和y=sin|x|(如图2)的图象，二者叠加得图3，图3即是y=|sinx|+sin|x|的图象，由图3，知ymin=0,ymax=2.

需要特别注意的是，应用图象分析法，除了要对基础知识深刻理解外，还应该对图象及其变化趋势有准确的把握.否则出现错误就在所难免.

六、利用数形结合，构造立体图形解题

有些代数问题，其几何意义不是一眼就看出来的，则需要灵活运用已学过的数学知识，进行适当的变形和巧妙构想，使这个代数表达式具有几何意义.

例9 已知正实数a、b、c、d满足a2+b2+c2=d2.

分析由已知a2+b2+c2=d2容易联系到长方体的对角线定理，不妨构造一个三棱分别为a、b、c的长方体，则对角线长为d.根据三角形两边之和大于第三边的结论，命题就可得证.

在数形结合教学中，通过各种例子，培养学生思维的灵活性，不断地提高巧妙的运用数形结合知识的能力.有的“数”其几何意义不是一眼就看出的，就需要灵活运用已学过的知识，进行适当的变形和巧妙构思，使“数”有几何意义，要重视数形结合训练，这对于学生分析问题和解决问题能力的培养和提高具有重要的意义，对于发展和培养学生的发散思维和一题多解能力有重要作用.

当然，上面所举的例子只是众多题型的一小部分，其分析问题、解决问题的能力还需同学们在解题中多摸索和多训练.

参考文献：

[1]郑金洲.基于新课程的课堂教学改革[M].福州：福建教育出版社，2003.