ITD和自适应广义形态滤波的特征提取方法*

黄新奇， 张亚飞， 毛存礼， 黄刚劲， 郭月江， 杨红艳

0 引 言

滚动轴承作为旋转机械设备重要的部件之一，其运行状况直接影响整个机械设备的运行。提前诊断出轴承是否发生故障对避免发生生产事故具有重要的意义[1，2]。因此，能够有效地提取轴承早期微弱故障特征，准确判断轴承发生故障位置是故障诊断领域的难点与热点。

郝如江等人[3]利用形态滤波器对滚动轴承故障信号进行特征提取，取得了良好的效果。宋平岗等人[4]采用经验模态分解(empirical mode decomposition，EMD)滤除噪声和低频干扰，通过自适应形态学滤波方法进行分析，提取了故障特征频率。沈长青等人[5]将集合经验模态分解(ensemble EMD,EEMD)与改进形态滤波相结合，有效提取了轴承微弱故障特征，但EEMD存在模态混叠及形态滤波器存在输出偏移问题，导致边频带的提取效果不理想。崔宝珍等人[6]将轴承故障故障信号通过广义形态滤波进行降噪预处理，然后进行EMD，选取包含故障特征丰富的固有模态函数(intrinsic mode function,IMF)分量信号进行边际谱分析，但广义形态滤波具有加权系数选取的不确定性，导致输出仍存在偏倚现象。

本文提出了一种本征时间尺度分解(intrinsic time-scale decomposition,ITD)和自适应广义形态滤波结合的新方法提取轴承的故障特征。通过ITD将采集的轴承故障信号分解成若干固有旋转(proper rotation,PR)分量；利用峭度准则选取若干PR分量进行重构；通过自适应广义形态滤波对重构后信号进行降噪处理并对其进行Hilbert包络谱分析，以提取故障特征信息。实例验证表明：本文方法可有效提取滚动轴承故障特征信息，提高了滚动轴承故障诊断的精度，具有一定的工程实用性。

1 ITD原理与方法

1.1 ITD

设Xt=[x1,x2,…,xn]为待测试信号，并将L定义为基线提取算子。信号的均值曲线表示为LXt，简记为Lt，则信号Xt进行ITD为Xt=Lt+Ht，Ht=Xt-Lt,Ht定义为合理的PR分量。

1)确定测试信号Xt的极值Xk及其所对应时刻τk，k为极值点个数，定义信号的分段线性基线提取因子L为[7,8]

(1)

(2)

式中t∈(τk,τk+1)；α为控制提取固有旋转分量幅度的增益控制参数，0﹤α﹤1，通常取0.5。

2)利用已得的基线分量Lt可得PR分量Ht为

Ht=(1-L)Xt=Xt-Lt

(3)

3)将Lt作为原始信号，重复上述步骤进行再次分解，直至基线分量单调，停止分解。

4)经过多次ITD，待测信号分解成若干PR分量和一个单调趋势之和，分解结果表示为

(4)

1.2 分量信号选取

对采集的振动信号通过ITD得到若干PR分量信号，其中,部分分量信号中包含丰富的故障特征信息，同时也存在大量的噪声，需进行降噪处理[8]。

峭度(kurtosis)为无量纲参数，能反映振动信号分布特性，其值大小可用于分析滚动轴承信号中所包含冲击成分的多少，数学定义如下[9]

(5)

式中x为待分析的振动信号;μ为信号x的均值;σ为信号x的标准差。

由于峭度对冲击信号特别敏感，适用于滚动轴承早期微弱故障振动信号分析。当滚动轴承无故障运行时，振动信号幅值分布接近正态分布，值约为3；当出现早期微弱故障时，滚动轴承振动信号幅值分布明显偏离正态分布，峭度值随之增大[10]。峭度指标越大的故障信号，信号中包含的冲击成分越多，滚动轴承故障信息包含于冲击成分当中。利用峭度选取PR分量有利于突变信息的特征提取。

2 自适应广义形态滤波

2.1 广义形态滤波

假设输入序列f(n)是定义在F=(0,1,...,N-1)上的离散信号，g1(n),g2(n)为不同的结构元素，广义形态学滤波器的定义如下[11]

(6)

(7)

广义形态开—闭结构的滤波器会造成输出偏小，而广义形态闭—开结构的滤波器造成输出偏大。为了有效解决上述问题，用将2种滤波器先加权和再求平均值，即

z(n)={GOC(f(n))+GCO(f(n))}/2

(8)

2.2 自适应广义形态滤波

在实际工程应用中，广义形态滤波器存在采用加权系数选取的不确定性的问题，会存在输出偏移现象，导致对滚动轴承振动信号降噪效果并不理想[13]。因此,本文采用最小均方(least mean square,LMS)算法处理2种广义形态滤波器的加权组合形式中权系数的确定问题[6]。其结构示意如图1所示。

图1 自适应广义形态滤波

令某待测信号为x(n)=s(n)+d(n)，其中,s(n)为无噪声的理想信号，d(n)为含噪信号

e(n)=s(n)-y(n)

(9)

式中e(n)为理想信号;s(n)为与滤波器输出信号y(n)间的误差信号。

令y1=GOC[x(n)]，y2=GCO[x(n)],有

(10)

输出信号的均方差为

E[e2]=E[|s(n)-y(n)|2]

(11)

采用LMS算法，取单个误差样本平方e2(n)作为均方误差E(e2(n)]的估计，并计算相对权系数的导数

(12)

通过最陡坡下降法优化权系数，可得

(13)

将式(12)代入式(13)可得

ai(n+1)=ai(n)+2μyi(n)e(n),i=1,2

(14)

式中μ为控制收敛速度的参数。

3 特征提取方法

故障特征提取具体步骤如下：

1)利用传感器分别采集现场滚动轴承内圈、外圈故障信号；

2)对故障信号进行ITD，分解成若干PR分量;

3)选取若干峭度值较大的PR分量，并对其进行重构;

4)对重构后的信号通过自适应广义形态滤波进行降噪处理；

5)对降噪后的信号进行Hilbert包络谱分析。

4 实列验证分析

为了验证本文方法的有效性，分别对实际采集的滚动轴承外圈信号和内圈信号进行分析。实验数据采用美国Case Western Reserve University的轴承数据[14]进行验证，轴承型号为6205—2RA JEM SKF，其参数详见表1。通过电火花技术在轴承内圈、外圈上各加工0.279 4 mm深，直径为0.177 8 mm的小槽，模拟轴承内圈、外圈局部裂纹故障。采样频率为48 kHz，转频173 0 r/min。通过上述参数计算可得到轴承外圈故障频率为103.36 Hz；内圈故障频率为156.14 Hz。

表1 6205—2RS JEM SKF型轴承参数

4.1 外圈故障分析

将采集到的轴承故障信号通过ITD，分解为4个分量，如图2所示。可以看出：外圈故障信号得到了有效地分解，但存在噪声干扰，需要进一步处理。分别计算4个分量的峭度值，如表2所示。可以看出：PR1和PR2的峭度值较大，因此，选取PR1和PR2进行重构。通过自适应广义形态学滤波器对重构信号进行降噪处理，滤波后的时域波形如图3所示。可以看出：由于噪声污染原因，无法有效识别故障冲击成分，需要对其进行下一步处理。包络谱分析如图4，可以看出：圈故障特征频率为105.5 Hz及其7倍频，可以准确判别滚动轴承的故障类型为外圈故障。为了验证本文方法的优越性，与文献[4]的实验结果进行了对比,如图5所示,可以看出：虽然文献[4]可以找到外圈的故障特征频率105.5 Hz及2倍频，但倍频幅值较小，高频部分被噪声淹没，特征提取效果不理想。

图2 外圈故障信号ITD

ITD分量信号PR1PR2PR3PR4外圈峭度值12.945.633.562.95内圈峭度值9.764.593.563.08

图3 自适应广义形态滤波后的重构信号

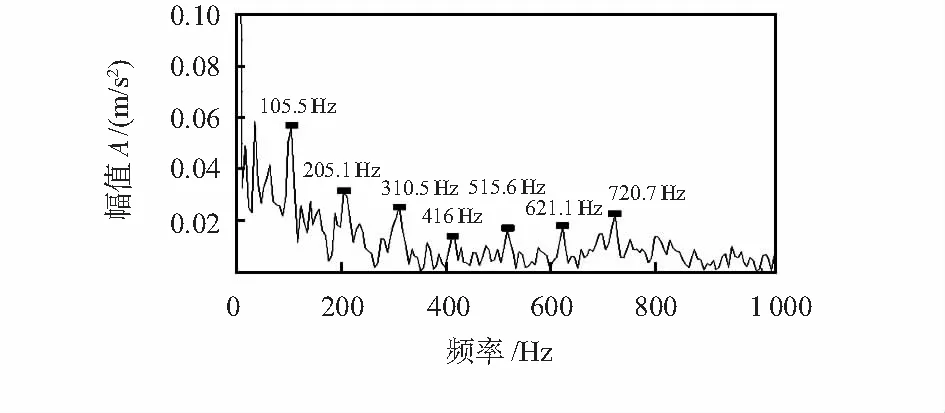
图4 Hibert包络谱分析

图5 参考文献[4]Hibert包络谱分析

4.2 内圈故障分析

将采集的轴承故障信号通过ITD，分解为4个分量，如图6所示。可以看出：内圈故障信号得到了有效地分解，但存在噪声干扰，需要进一步处理。分别计算4个分量的峭度值，如表2所示。可以看出PR1和PR2的峭度值较大，因此，选取PR1和PR2进行重构。通过自适应广义形态学滤波器对重构信号进行降噪处理，滤波后时域波形如图7。可以看出：由于噪声污染原因，无法有效识别故障冲击成分，需要对其进行下一步处理。包络普分析如图8，可以看出：内圈故障特征频率为152.3 Hz及其7倍频，可以准确判别滚动轴承的故障类型为内圈故障。为了验证本文方法的优越性，与文献[4]的实验结果对比如图9所示。可以看出：文献[4]虽然可以找到内圈的故障特征频率152.3 Hz及3倍频，但高频部分被噪声淹没，特征提取效果不理想。

图6 内圈故障信号ITD

图7 自适应广义形态滤波后的重构信号

图8 Hibert包络谱分析

图9 文献[4]Hibert包络谱分析

5 结 论

1)将ITD和自适应广义形态滤波相结合用来提取滚动轴承的故障特征。通过ITD将采集到的轴承故障信号分解成若干PR分量；利用峭度准则选取故障特征丰富的PR分量进行重构。重构后的信号通过自适应广义形态滤波进行降噪处理并对其进行Hilbert包络谱分析，二者结合发挥了各自的优点。

2)利用本文的方法分别对滚动轴承的内圈和外圈进行故障特征提取，可有效提取到故障的基频及倍频部分。与其他方法对比，本文方法提取的准确率更高，噪声抑制效果更好，提高了滚动轴承诊断的精度。

参考文献:

[1] 马文龙,吕建新,吴虎胜,等.多传感器信息融合在滚动轴承故障诊断中的应用[J].传感器与微系统,2013,32(7):132-135.

[2] 丁国君,王立德,申 萍,等.基于EEMD能量熵和LSSVM的传感器故障诊断[J].传感器与微系统,2013,32(7):22-25.

[3] 郝如江,卢文秀,褚福磊.形态滤波器用于滚动轴承故障信号的特征提取[J].中国机械工程,2009(2):197-201.

[4] 宋平岗,周 军.基于EMD和LMS自适应形态滤波的滚动轴承故障诊断[J].科学技术与工程,2013,13(6):1446-1452.

[5] 沈长青,谢伟达,朱忠奎,等.基于EEMD和改进的形态滤波方法的轴承故障诊断研究[J].振动与冲击,2013,32(2):39-43.

[6] 崔宝珍,马泽玮,李会龙,等.基于广义形态学滤波和Hilbert边际谱的滚动轴承故障诊断[J].中国机械工程,2016(11):1484-1488.

[7] Frei M G,Osorio I.Intrinsic time-scale decomposition:Time-frequency-energy analysis and real-time filtering of non-stationary signals[J].Proceedings of the Royal Society of London A,2006,463:321-342.

[8] 齐 鹏,范玉刚,冯 早.基于ITD和敏感SVD的故障诊断方法研究[J].华中师范大学学报:自然科学版,2016,50(6):818-825.

[9] 吴小涛，杨 锰，袁晓辉，等．基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J]．振动与冲击，2015，34(2)：38-44．

[10] 胡爱军,马万里,唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J].中国电机工程学报,2012,32(11):106-111.

[11] 马泽玮,崔宝珍.基于广义形态学滤波和EEMD分解的滚动轴承故障诊断[J].中国农机化学报,2015(2):269-273.

[12] Raj S,Murali N.Early classification of bearing faults using morphological operators and fuzzy inference[J].IEEE Transactions on Industrial Electronics,2013,60(2):567-574.

[13] 张金敏,翟玉千,王思明.小波分解和最小二乘支持向量机的风机齿轮箱故障诊断[J].传感器与微系统,2011,30(1):41-43.

[14] Case Western Reserve University Bearing Data Center.Bearing data center fault test data[EB/OL].[2009—10—01].http:∥www.eecs.case.edu/laboratory/bearing.