基于相位自校正的MEMS陀螺仪温度补偿方法*

林跃杉， 尹 韬， 吴焕铭， 杨海钢

0 引 言

微机电系统(micro-electro-mechanical system,MEMS)陀螺仪传感器采用硅制作，当温度变化时，传感器的工作状态改变，影响陀螺仪的性能。因此，须进行温度补偿。2009年，Xia D Z等人通过分析温度对MEMS器件的杨氏模量的影响提出了一个Q值与温度的经验公式，并通过标定得到了温度和偏置之间的经验公式，在检测环路使用双环闭环补偿对陀螺仪系统进行补偿，补偿后的温度灵敏度到达了0.03°/h/℃[3]。2011年,Fan Y Z等人提出了一种结合锁相环(phase locking loop,PLL)和可变延时模块对驱动环路的频率进行补偿，使其驱动环路的频率尽可能接近驱动轴的谐振频率[4]。2014年,Wen M等人更进一步对系统进行了详细分析，分别就陀螺仪和电路进行了分析，得出温度变化是影响整个系统零偏的最大因素[5]。同年,Zotov Sergei A等人提出了将驱动轴的频率作为“温度计”的方法对电路进行补偿的方法，并结合SBR补偿和正交误差补偿的方法来实现整体的补偿[6]。2015年,He C H等人提出了一种改进温度对Mode-Match影响的方法，在-40～80 ℃之间可以达到误差小于0.32 Hz[7]。2016年,Fontanella Rita等人提出了一种基于反向传播(back propagation,BP)网络的标定方法来克服温度带来的影响[8]。

然而，上述方法或需要增加专门测量温度的电路，或是采用了电路中的某个不稳定指标用于度量温度，又或是方法复杂，不易与MEMS陀螺仪进行集成。本文提出一种改正解调相位误差的方法，充分利用正交输出数据，建立正交输出数据与相移之间的关系，实现对电路偏置的补偿。

1 原 理

主流的MEMS陀螺仪为谐振式陀螺仪，其工作原理可以简化成二维自由度的机械振动器。其示意图如图1所示。由于在MEMS陀螺仪加工工艺存在偏差，实际上驱动轴(x轴)与检测轴(y轴)并不是完全正交的。因而，驱动驱动轴振荡的力会耦合到检测轴中，引起检测轴产生一定的位移。考虑由x轴耦合到y轴的弹性系数和阻尼系数kyx和Dyx。当MEMS陀螺仪以Ωz的角速度绕z轴进行旋转时，受哥式力为-2Ωzmx′，其检测轴方程为

my″+Dyyy′+Dyxx′+kyyy+kyxx=-2Ωzmx′

(1)

在谐振式MEMS陀螺仪工作时，驱动轴进行简谐运动，x轴位移与速度之间存在90°的相位差，因此,由于哥式力-2Ωzmx′和弹性力-kyxx所引起的输出信号是正交的，可以通过解调实现分离,分别得到同相(in-phase，I路)和正交(quadrature，Q路)的输出。其中,I路输出信号VRate包含了角速度信息，而Q路输出信号VQuadrature包含了机械正交误差的信息，VRate和VQuadrature其分别为

(2)

2 基于相位自校正改善偏置灵敏度的方法

假设哥式力信号与解调信号间的相位差为Δθ，经解调和低通滤波后的VRate和VQuadrature信号为

(3)

由于在加工过程中不可避免会引入机械正交误差，而且Bkyx往往很大，会造成I路有一个比较大的偏移量，并且在一定程度上影响了陀螺仪系统的量程。由于两个交调幅信号Bkyx≫AΩZ，且Δθ不是很大，式(3)简化为

(4)

可以看出，由于VQuadrature与Δθ是余弦关系，当Δθ最小时，VQuadrature应该取到最大值。通过解调出VQuadrature的信号，当VQuadrature取得最大值时，相位差就可以近似认为最小，从而减小由于相位误差对系统的稳定性和量程带来的不利影响。

根据MEMS陀螺仪偏置的定义，输出的偏置电压为

(5)

如图2所示，在进行相位改正之前，由于温度T1和T2所引起的θ(T1)和θ(T2)之间的差比较大，反映在偏置上就是其漂移比较大，而通过相位改正之后相位θ′(T1)和θ′(T2)之间的相位差较小，引起的偏置的漂移也相应地减小甚至消除，因此，通过对Δθ的改正就能将温度引起的偏置变化减小，即降低偏置的温度敏感度系数。此方法的流程如图3所示。

图2 温度引起的偏置变化示意

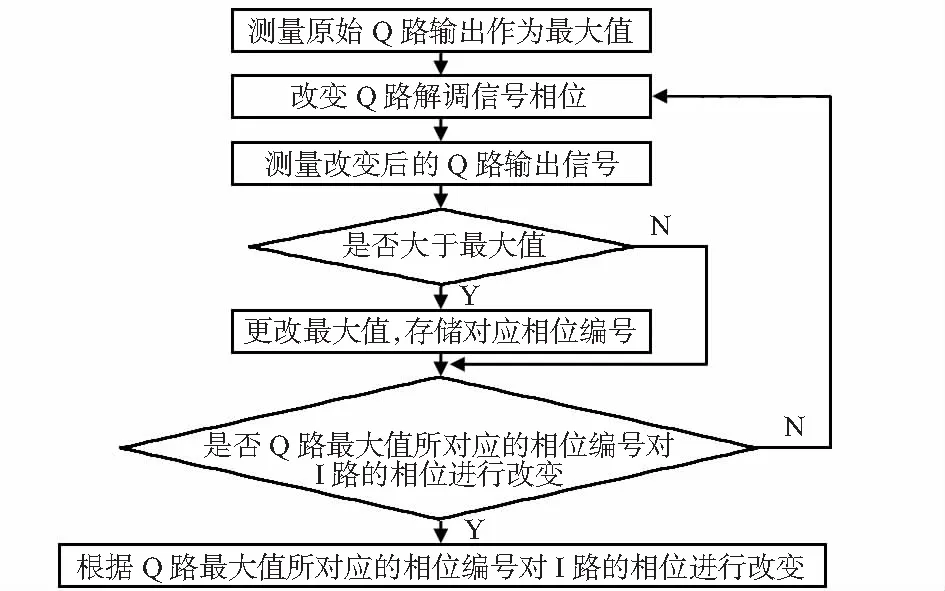
图3 温度补偿方法流程

该方法的系统示意图如图4所示，包括MEMS陀螺传感器、驱动电路和检测电路；为了保证驱动频率和驱动幅度的稳定，驱动电路与MEMS陀螺传感器一起构成闭环，相当于一个“机械—电学”振荡器；检测电路则采用传统的包络检波电路实现。其中，闭环驱动由检测前端、可变增益放大器(variable-gain amplifier,VGA)、比例—积分(proportional integral,PI)控制器、整流器等构成，输出作为PLL的输入产生I/Q路解调信号；开环检测电路一般由检测前端、解调器、仪表放大器和低通滤波器等组成。控制器需要完成对数据的采样，并对一段时间内的输出取均值，最后需要进行比较取出最大值所对应的相位编码进而控制PLL。

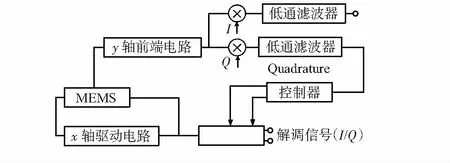
图4 基于相位自校准温度补偿方法系统框图

3 MATLAB仿真

采用MATLAB的Simulink对上述方法进行了仿真。Simulink模型使用检测通路与控制器模型相结合，采用理想的正弦波模拟驱动轴的振动位移，同时使用多组不同相位的正弦波模拟相位的改变，以实现PLL的功能，通过Switch选择不同的相位的解调信号进入解调器，同时使用控制器进行Q路输出最大值的检测，根据最大值输出相应的模拟解调信号的选择控制码。其示意图如图5所示。

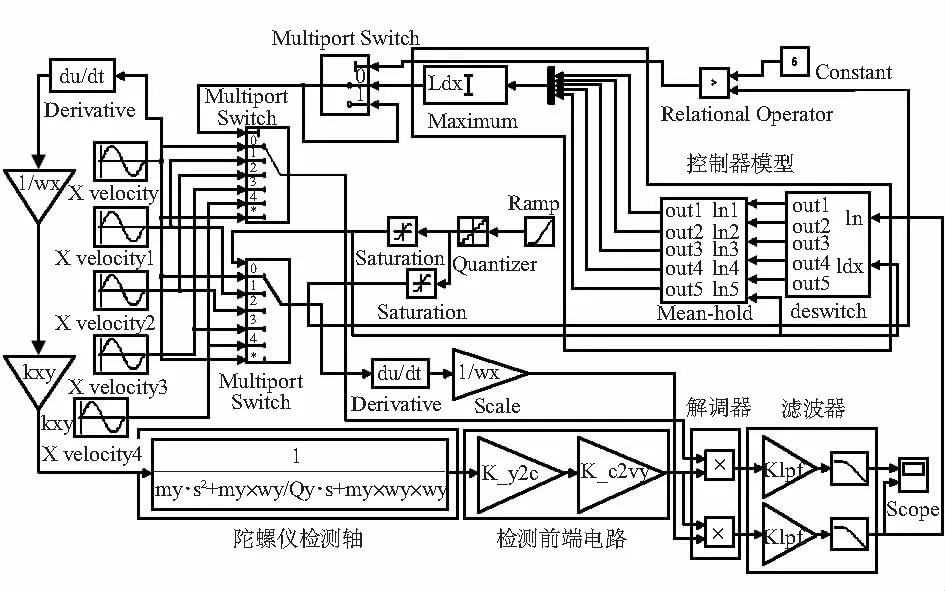
图5 Simulink模型系统框图

设置不同的检测轴品质因子Q值模拟温度变化引起的影响，Q值分别为10,15,20,25 和30，其I路的输出如图6所示，在输入角速度为0°的情况下，可以看到经过自校正，其偏移减小，改善了由于正交误差引入的量程损失，并且由于温度变化即品质因子Q值变化引起的偏置漂移减小，从0.19 V下降到0.06 V。图7为品质因子Q值为20的Q路输出，使用了5组的相位(编号从0开始，相位依次变大)进行改正，可以看到通过修改解调相位确实可以改变Q路的输出，在编号为2的相位处其输出最大，根据拟合曲线，可以看到其输出与解调相位间呈现出类似余弦函数的形状，与前期结论相符。

图6 Simulink仿真I路输出结果

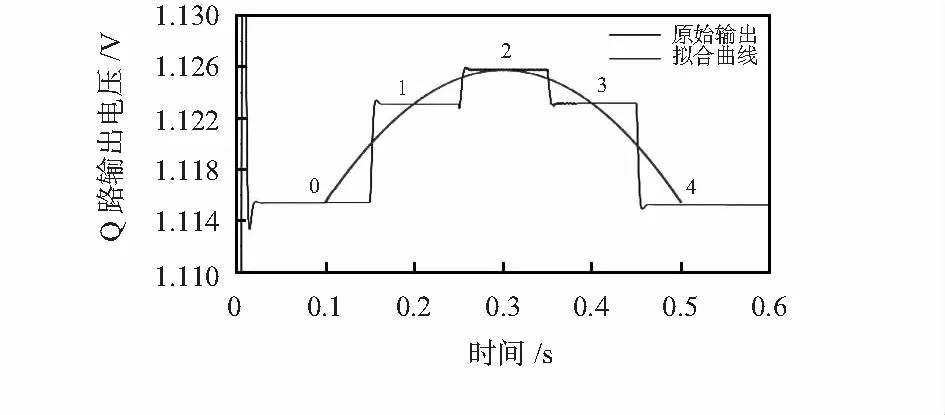
图7 MATLAB仿真Q路输出结果

4 测试结果

测试的系统由MEMS陀螺仪承载板和MSP430开发板组成。其中MEMS陀螺仪驱动、检测芯片均采用Global Foundries公司的0.35 μm标准CMOS工艺制作[9]，电源电压为5 V。为了产生多个延时信号，PLL通过在分频器单元中采用移位寄存器技术实现解调信号相位的矫正功能。控制电路采用MSP430开发板实现。系统如图8所示。由于驱动检测芯片的电压是5 V，而MSP430的输出电压为3.3 V，因此,在两个系统板之间使用了一个电平转换模块。

图8 测试系统实物

使用数字万用表对系统的偏置输出进行连续测量，艾伦方差如图9所示，补偿前的偏置稳定性bs为26.04°/h，补偿后偏置稳定性为26.18°/h，可以看出经补偿前和补偿后的偏置稳定性没有明显的变化。

图9 艾伦方差

温度测试采用热流罩对PCB整体进行加热或者降温，偏置结果如图10所示，在-10～30 ℃温度范围内，可以看出:在改正前的偏置的温度系数Ts为1.93°/h/℃，经过相位改正后，其偏置的温度系数下降到了0.01°/h/℃，下降了近20倍。

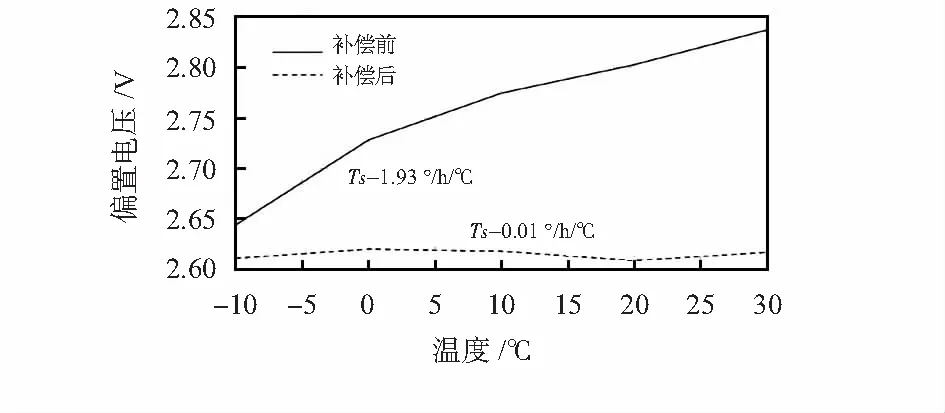
图10 温度补偿结果

5 结 论

本文提出了一种基于正交输出的改进MEMS 陀螺仪系统输出偏置的温度灵敏度方法，简单易行，仅需要在开环检测的基础上增加正交检测通路和简单控制电路即可对温度进行补偿，且补偿前后偏置的温度灵敏度从1.93°/h/℃下降到了0.01°/h/℃，下降了近20倍。

参考文献:

[1] Söderkvist J.Micromachined gyroscopes[J].Sensors and Actuators A:Physical,1994,43(1):65-71.

[2] Wen H Ko.Trends and frontiers of MEMS[J].Sensors and Actuators A:Physical,2007,136(1):62-67.

[3] Xia D Z,Yu C,Wang Y L,et al.A digitalized silicon microgyroscope based on embedded FPGA[J].Sensors,2012,12:13150-13166.

[4] Fan Y Z,Luo B,Wang A C.Analysis of temperature adaptability for frequency control loop for silicon micromechanical gyro-scope[C]∥Electronic Measurement & Instruments(ICEMI),2011:346-349.

[5] Wen M,Wang W H,Luo Z,et al.Modeling and analysis of temperature effect on MEMS gyroscope[C]∥Electronic Components and Technology Conference(ECTC),2014:2048-2052.

[6] Zotov Sergei A,Simon Brenton R,Sharma Gunjana,et al.Utilization of mechanical quadrature in silicon MEMS vibratory gyroscope to increase and expand the long term in-run bias stabi-lity[C]∥2014 International Symposium on Inertial Sensors and Systems(ISISS),2014:1-4.

[7] He C H,Zhao Q C,Huang Q W,et al.A MEMS vibratory gyroscope with real-time mode-matching and robust control for the sense mode[J].IEEE Sensors Journal,2015,15(4):2069-2077.

[8] Fontanella Rita,Domenico Accardo,Caricati Egidio,et al.An extensive analysis for the use of back propagation neural networks to perform the calibration of MEMS gyro bias thermal drift[C]∥2016 IEEE/ION Position,Location and Navigation Symposium(PLANS),2016:672-680.

[9] 吴焕铭,杨海钢,尹 韬,等.一款基于AGC-PI结构的微陀螺闭环驱动电路芯片[J].纳米技术与精密工程,2014,12(1):56-62.