串联机械臂关节故障快速判定方法研究*

李铭浩, 敖天翔, 刘满禄,2, 张 华

0 引 言

实际应用中机械臂关节故障属于较为常见的故障，其中包括执行器故障与传感器故障[1～3]。针对于可重构机械臂，杜艳丽[4]利用迭代故障观测器估计期望位置，利用位置误差信息判断错误类型。张甲子[5]通过使用龙博格观测器观测执行器误差与传感器实现对错误类型的判别。郭刚[6]针对二自由度机械手的多模型故障，设计无色卡尔曼滤波器进行状态跟踪，并使用广义贝叶斯网络进行信息融合，得到故障最优估计结果。Gspandl S等人[7]基于Indi Golog框架和历史故障信息设计置信管理系统，根据不同故障的置信不同进行故障判别。Wu Y,Fu Z等人[8]利用小波包分解对机器人运动误差信号进行分解，提取每个节点的能量，形成特征向量，结合Hidden Markov模型获得故障信息。O'Keeffe J等人[9]提出了一种基于行为特征向量法的群故障诊断方法，可以诊断常见的机电故障类型。Van M等人[10]基于神经网络滑模观测器研究了鲁棒故障诊断算法，降低了滑模的抖振，提高了收敛性。

上述算法均较为庞大且故障估计结果以理论模型为主，不太符合工业机械臂的实际应用。本文通过建立平面机械臂的运动学和动力学模型，搭建反演控制器完成正常控制；针对机械臂在运行过程中某一关节突发未知故障，分析常见故障类型并建模。针对具体问题利用各个关节检测到的角度与角速度信号，搭建角度与角速度残差观测器，设定角速度残差阈值，实时检测残差信号，利用多个关节的残差突变情况，判断故障类型和位置。利用MATLAB和V-rep联合仿真平台，在正常运行机械臂中添加故障信号，通过50次随机故障验证算法的有效性和快速性[11]。

1 模型建立

1.1 运动学建模

机械臂的运动学模型描述了关节空间和操作空间的映射关系。本文使用基于运动学旋量的指数积 (product of exponential,POE)方法[12]建立机械臂运动学模型。整个系统只需2个坐标系：惯性坐标系{S}和与末端执行器固连的工具坐标系{T}。各个关节的运动由与之关联的关节轴线的运动旋量产生，由此可以得到其运动学的几何描述。以平面4R机械臂为例，如图1所示。

图1 4R机械臂模型

建立各个关节单位运动旋量为

(1)

式中w的第n列代表第n个旋转轴ξn的方向

(2)

γ的第n列代表第n个旋转轴ξn的某一个点的位矢。

由图1(b)建立坐标系{S}与{T}的转换关系为

(3)

令终点关节角度θ=[θ1θ2θ3θ4]，根据Rodrigues公式

(4)

(5)

根据式(4)和式(5)，可知各关节运动旋量

(6)

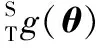
(7)

1.2 动力学建模

根据拉格朗日法[13,14]建立机械臂通用动力学模型

(8)

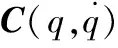
(9)

(10)

2 故障模型分析

本文考虑危险环境中较为常见的执行器和传感器故障。执行器故障和传感器故障均包括锁死、恒增益和恒偏差故障[4,5]。对此3种故障形式进行建模，以执行器故障为例，传感器故障模型与其相似。

1)卡死故障：第i个执行器锁死故障模型为

(11)

(12)

2)恒增益故障：第i个执行器恒增益故障模型

(13)

式中λ∈[0,1]为失能因子。在η(t-T)=1时，若λ=0，表示完全失能，即为自由摆动故障；若λ=1，表示正常；若0<λ<1表示部分失能，即恒增益故障。

3)恒偏差故障：第i个执行器恒偏差故障模型为

(14)

式中ei为偏差常数。

3 残差观测器设计

考虑最为严重的执行器和传感器锁死故障(不考虑传感器完全无反馈信号情况)，二者外在表现形式一致：某一关节的角度传感器反馈值为一常数，速度反馈值为0。

搭建速度残差观测器[15]。改写式(8)为如下形式

(15)

(16)

为完成后续残差观测器的设计及验证，首先设计反演控制器[16，17]步骤如下：

(17)

(18)

式中K2>0为反馈增益。

对系统进行离散，设计离散系统观测器

x(n+1)=Ax(n)+Bτ-K(x(n)-Q(n))

(19)

R(n)=e(n)-Te(n-1)

(20)

通过检测R(n)的值是否发生突变可以表明期望运动与实际运动的突变情况。

4 仿真验证

在MATLAB和V-rep联合仿真环境中搭建4连杆平面机械臂模型，连杆长度为[1;1;1;1]m，连杆质量为[1;1;1;1]kg，取各关节初始位形为[0;0;0;0]，最终位形为[π/3;π/3;π/3;π/3]，无故障如图2所示。采用五次多项式插值算法进行轨迹规划，规划时间30 s，为各个关节的位置，速度传感器添加0.02 rad幅度的白噪声模拟外部干扰。

搭建MATLAB控制系统，建立式(7)和式(8)中所述数学模型，采用式(18)控制律、式(19)观测器，其中各项参数为K1=K2=I4×1；Krq=Krv=I4×4；Koq=Kov=2I4×4。

1) 正常情况下的位置、速度以及速度残差如图3和图4所示。

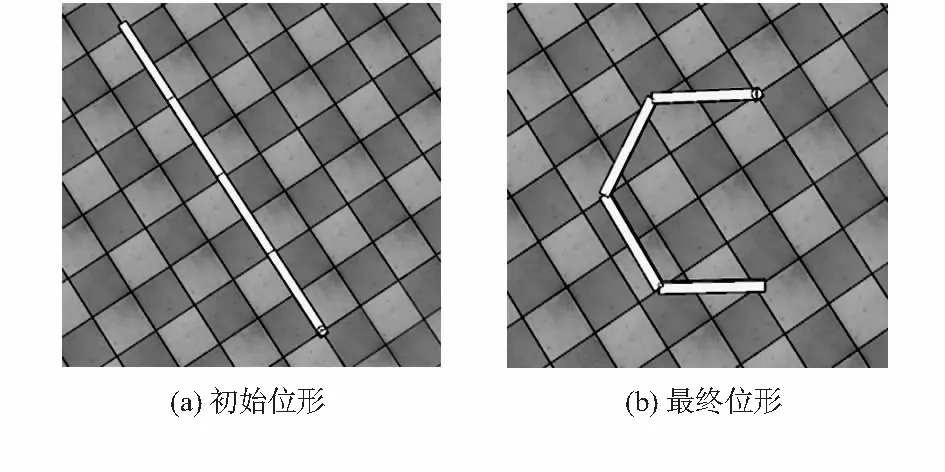
图2 4R平面机械臂V-rep模型

图3 正常情况下各关节位置和速度

图4 正常情况下各关节速度残差

2) 以第10 s第2关节分别出现执行器、传感器锁死故障为例。实验结果如图5、图6所示。

图5 第2关节执行器锁死故障速度残差

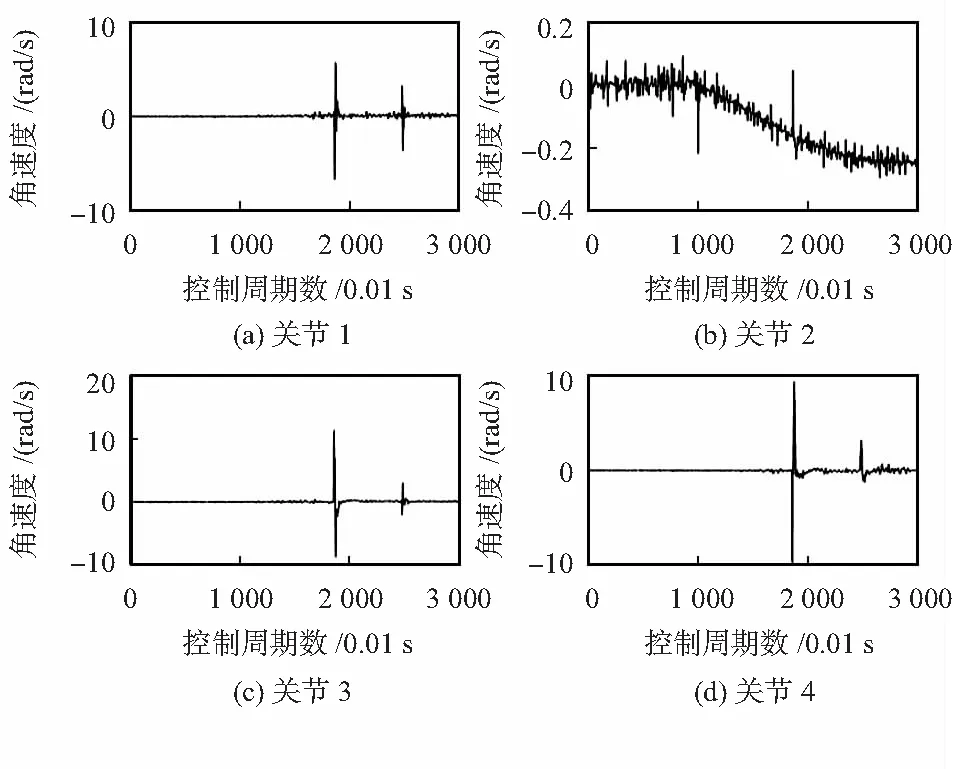
图6 第2关节传感器锁死故障速度残差

3)再以第20 s第4关节分别出现执行器、传感器锁死故障为例。实验结果如图7、图8所示。

图7 第4关节执行器锁死故障速度残差

图8 第4关节传感器锁死故障速度残差

根据上述实验结果可知，在不发生故障时，机械臂残差观测器的观测值一直处于固定范围内且无明显跳变。加入故障信号后，故障关节会在故障发生的下一个控制周期内出现大幅跳变。在同一时间范围内，对于执行器锁死故障，各个关节均会发生跳变，并且发生故障的关节会突变一极小值；对于传感器锁死故障，仅故障关节发生跳变为一极小值。设置一上下阈值为-0.12～+0.12 rad/s，设置不同的时间点、关节和故障类型上进行50次实验，50次实验均能在2个控制周期内得到正确的故障警报，证明该算法的快速性和准确性。

5 结 论

本文使用POE方法和拉个朗日法建立平面机械臂的运动学和动力学模型并设计反演控制器进行控制。实验证明可以在两个控制周期内快速的反馈故障类型和位置，为后期决策提供支持。

参考文献:

[1] 毛海杰,李 炜,冯小林.非线性系统主动容错控制综述[J].传感器与微系统,2014,33(4):6-9，13.

[2] 陈拥军,袁慎芳,吴 键,等.无线传感器网络故障诊断与容错控制研究进展[J].传感器与微系统,2010,29(1):1-5.

[3] 张娅玲,陈伟民,章 鹏,等.传感器故障诊断技术概述[J].传感器与微系统,2009,28(1):4-6，12.

[4] 杜艳丽.考虑多故障同发的可重构机械臂分散主动容错控制[D].长春：吉林大学，2014.

[5] 张甲子.基于故障观测器的可重构机械臂主动容错控制方法研究[D].长春：吉林大学，2013.

[6] 赵 博.多故障并发的可重构机械臂主动分散容错控制方法研究[D].长春：吉林大学,2014.

[7] Gspandl S,Pill I,Reip M,et al.Developing concepts in applied intelligence[M].Berlin Heidelberg：Springer，2011:113-118.

[8] Wu Y,Fu Z,Liu S,et al.Intelligent robotics and applications[M].Berlin Heidelberg:Springer International Publishing,2016.

[9] O'Keeffe J,Tarapore D,Millard A G,et al.Towards fault diagnosis in robot swarms:An online behaviour characterisation approach[C]∥Conference Towards Autonomous Robotic Systems,2017:393-407.

[10] Van M,Kang H J,Suh Y S,et al.A robust fault diagnosis and accommodation scheme for robot manipulators[J].International Journal of Control Automation & Systems,2013:11(2):377-388.

[11] 王 宪,杨国梁,张方生,等.基于牛顿—拉夫逊迭代法的6自由度机器人逆解算法[J].传感器与微系统,2010,29(10):116-118，131.

[12] 于靖军,刘辛军,丁希仑.机器人机构学的数学基础[M].2版.北京：机械工业出版社,2015.

[13] Bruno Siciliano.机器人学:建模、规划与控制[M] 西安：西安交通大学出版社,2013:177-218.

[14] Craig J J.机器人导论[M].北京：机械工业出版社,2016：48-70.

[15] Robert L W，Douglas A L.线性状态空间控制系统[M].西安：西安交通大学出版社，2014：300-350.

[16] Zhou J,Wen C.Adaptive backstepping control of uncertain systems[M].Berlin Heidelberg:Springer.2008.

[17] 刘金琨.机器人控制系统的设计与MATLAB仿真[M].北京：清华大学出版社,2008.