谈两个特殊行列式在教学中的运用

孙忠洋

（淮北师范大学数学科学学院，安徽淮北 235000）

行列式的计算方法很多，综合性较强，需要我们多观察总结，往往运用一些特殊的行列式，在化简复杂的行列式中会起到化繁为简的计算效果，培养学生兴趣和思维，对大学的教学起到积极的作用。在此主要谈了“爪”字形和“么”字形行列在教学中的运用。

1 两种特殊行列式在教学中的运用

一般情况下，传统的教学方式基本上都是运用行列式的定义或性质，逐步求解行列式，对于简单的行列式可以快速求解，但对于较为复杂的行列式往往无法起到快速求解的目的，这就需要熟练掌握一些特殊的行列式的运算方法，对求解复杂行列式会起到事半功倍的效果。 在很大程度上，培养了学生的兴趣和学习的积极性，有利于培养学生的解题思维。

1.1 “爪”字形行列式

在高等代数和线性代数中，有两种非常特殊的行列式，首先介绍“爪”字形行列式。

行列式的特点：行列式中的非零元素排列形状如“爪”字形。

解题方法：将每行（或每列）的元素都乘以一个倍数，然后都加到第i行（或第i列），并提取第i行（或第i列） 元素的公因子，再进行计算。下面讲解“爪”字形行列式的计算，如下：

例 1：计算（n+1） 阶行列式：）后都加到第1列，有

解法 1： 将第 i＋1（i=1，2…，n）列乘以

注：许多行列式可经适当变形化为“爪”字形行列式，此行列式在教学中具有重要的作用，但需要注意，在方法1的证明中一定要应用条件：ai≠0（i=1，2…，n）， 但是在方法 2 的证明中， 不需要使用已知条件：很多行列式可以化成“爪”字形行列式，然后再进行简化计算，见下题。

例2：计算n阶行列式：

解法1：在原行列式中添加一行和一列后，从第2行开始直至第n+1行都加上第1行的（-1）倍，有

（1）式为“爪”字形行列式。下面分三种情况讨论：

（1）当xi≠ai（i=1，2，∧，n）时，将（1）式中第i+1（i=1，2，∧，n）列乘以）后都加到第1列，有

（2）当xi-ai（i=1，2，∧，n）中只有一个为0时，在（1） 式中假设存在一个i，使得xi-ai=0，对（1） 式的第i+1行展开，有

Dn=（x1-a1）（x2-a2）∧（xi-1-ai-1）ai（xi+1-ai+1）∧（xn-an）

（3） 当 xi-ai（i=1，2，∧，n）中有两个或两个以上xi-ai=0，假设在（1） 式中x1-a1=x2-a2=0，可知

（1） 式中存在两行相等，因此，Dn=0。

解法2：在原行列式中添加一行和一列后，从第2行开始直至第n+1行都减去第1行，有

关于“爪”字形行列式在教学中的运用还有很多，可以处理更加复杂的行列式，需要我们继续研究，“爪”字形行列式在行列式的计算中能起到化简复杂行列式的作用。

2.2 “么”字形行列式

行列式的特点：行列式中的非零元素排列形状如“么”字形。

解题方法：按某一行（或某一列）运用公式直接展开，可得结果。 下面讲解“么”字形行列式的计算。

例1： 计算（n+1） 阶行列式：

解： 按第1列展开，有

例2：计算n阶行列式：

解：按第1行展开，有nxn-1+（n-1）xn-2+∧+2x+1

注：许多行列式也可经适当变形化为“么”字形行列式，例1和例2是“么”字形行列式的基本计算方法，对于“么”字形行列式在教学中的运用，可见例3。

例3：计算n阶行列式：

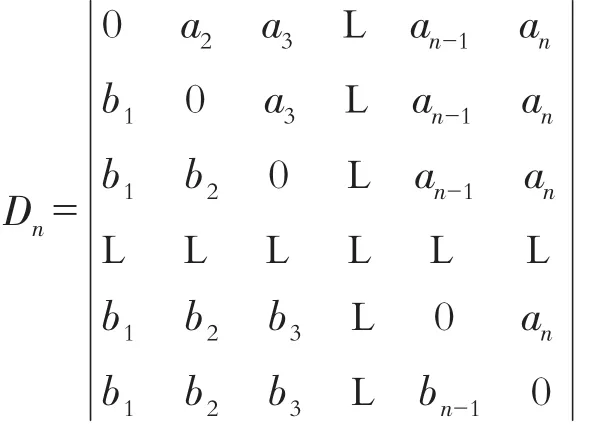
解：从第n-1行开始直至第2行，每行乘（-1）加到下一行，再按第1列展开，有

把“么”字形行列，按第1行展开有

Dn=（-1）n+1[b1a2a3Lan+b1b2a3Lan+L+b1b2Lbn-1an]

例4： 计算n阶行列式：

解： 从第n-1行开始直至第1行，每行（-1）乘加到下一行，再按第1列展开，有

再从第2列开始直至第n-1列都加到第1列，再按第1列展开，有

3 教学总结

行列式是高等代数和线性代数的重要教学内容，是求解线性方程组、逆矩阵和矩阵特征值的基础。在高等代数和线性代数的教学内容以及工程技术中都有着广泛的应用。在整个行列式的教学过程中，要注意总结教学中的重难点，总结特殊的行列式在教学中的运用，培养学生运用特殊的方法解决复杂问题的能力。在教学中，运用“爪”字形和“么”字形行列式在化简复杂的行列式中会起到化繁为简的计算效果。

[1]张禾瑞，郝炳新.高等代数[M].北京：高等教育出版社，2007.

[2]居余马，胡金德.线性代数[M].北京：清华大学出版社，2009.

[3]罗文俊.关于行列式的计算与讨论[J].贵州大学学报(自然科学版)，2003，20（2）： 123-126.

[4]张新功.行列式的计算方法探讨[J].重庆师范大学学报(自然科学版)，2011，28（4）： 88-92.

[5]李排昌，左萍.行列式与解线性方程组[J].中国人民公安大学学报(自然科学版)，2010，1（1）：100-102.