我国全要素生产率的估算及收敛性检验——基于DEA方法的实证分析

李 珂，杨 洋

（甘肃政法学院经济管理学院，兰州730010）

改革开放以来，中国经济持续高速增长，GDP从1978年的3 678.7亿元增长到2014年的181 182.5亿元，堪称“中国奇迹”。经济飞速增长的同时，地区间发展的不平衡现象日趋严重。这将给当下经济的进一步发展带来严峻挑战。为此，研究区域发展失衡背后的深层原因，将为缩小中国经济的区域发展差距，释放新的发展动能，具有重大的理论和现实意义。

新古典增长理论认为，经济持续增长主要依赖于全要素生产率的提升。为此，学界常以全要素生产率来衡量研究走势。全要素生产率（Total Factor Productivity）简称 TFP，指扣除土地、劳动、资本和原材料等要素投入以外的技术进步和效率提升等因素引起的产出增长。王志平指出，TFP的增长能够准确地测度效率的提升和技术的进步，反映生产率的变动[1]。TFP的估算方法主要有两类：一类是索洛（Solow）余值法，基于增长速度的方程测算；另一类是前沿生产函数法，基于TFP的变化进行测算，包括随机前沿分析（SFA）参数方法和数据包络分析（DEA）的非参数分析方法。传统测算TFP采用Solow余值法，即在产出中扣除了资本和劳动以外的剩余部分。该方法的缺陷在于生产单位和生产者在效率充分情况下进行决策的假定；该假定在应用时具有一定的局限性。并且运用Solow余值测算TFP时需选取具体的函数形式，可能导致函数选择不合理产生误差。基于此，学者们通常采用SFA和DEA分析方法。由于DEA的Malmquist方法无需做出假定和设置具体的函数形式，并将TFP的变化分解为技术效率提升和技术水平改进，从而使TFP增长源泉的研究更为深入。基于DEA分析方法，郭庆旺等的测算结果显示，1979—2013年中国省际间的TFP增长、技术效率和技术进步存在较大差异，且这种差异有逐步增加的趋势[2]；张煜等认为，2001—2012年中国的TFP呈现负增长，且技术进步的贡献明显高于技术效率，因此制约TFP的主要因素是技术效率的下降[3]；刘建国等对1990—2009年各省TFP的估算结果显示，整体而言中国的TFP平均下降了1.35个百分点，其中东部地区平均上升2.37个百分点[4]；颜鹏飞的测度结果显示1978—2001年中国TFP的年均增速为0.25%，且增长的源泉是技术效率的提高[5]。

与上述研究不同，本文以促进经济增长的全要素生产率为研究主题，选取2000—2014年间的省际面板数据，应用DEA的Malmquist指数法，测算全国及各省份的TFP变化率并考察其收敛性，以期得到经济增长背后的真正原因。

1 模型选取

DEA是一种非参数前沿分析法。通过这一方法可求出Malmquist指数。DEA的核心原理是在现有的投入产出数据下，根据决策单元偏离生产前沿面的范围来识别规模效率和最佳技术。Malmquist指数最初由Malmquist创造，被Caves和Fare等进行技术效率和生产率的提升研究[6]。Malmquist指数的形式为：

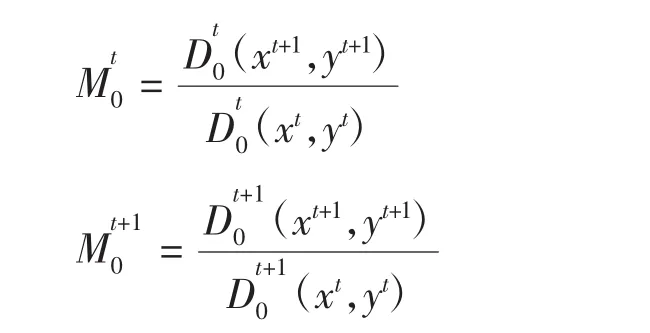
其中，Mt指数测度了以第t期为技术参照值时，从t—t+1期的全要素生产率的变化；Mt＋1指数测度了以第t+1期为技术参照值时，从t—t+1期的全要素生产率的变化。随后，Fare等人为避免参照技术选择的随机性，将Caves计算的Malmquist指数进行修改，将其确定为在第t期和第t+1期之间的几何平均数，具体为：

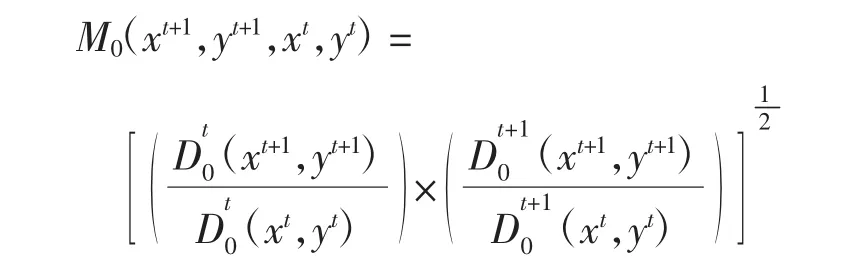
式中：M0（xt+1，yt+1，xt，yt）为TFP的变化率（TFPch）；xt和yt分别为投入向量和产出向量；当M0（xt+1，yt+1，xt，yt）〉1时，表示决策单元的生产率得到提升，即TFP提高；当M0（xt+1，yt+1，xt，yt）〈1时，表示决策单元的生产率降低，即TFP下降；当M0（xt+1，yt+1，xt，yt）＝1时，表示决策单元的生产率没有变化，即TFP不变。TFP的变化率（TFPch）分解为技术效率变化率（Effch）和技术进步变化率（Techch）两个指标，表示如下：

式中：Effch为第t—t+1时期的观测值与技术前沿面的相对变化程度，当Effch〉1时，表示技术效率提高，反之则技术效率下降。Techch为技术前沿面边界的改变程度。当Techch〉1时，表示技术进步率提高，反之表示技术进步率下降。上式是在规模报酬不变的前沿面得出的，当对应规模报酬可变的前沿面时，技术效率又分为纯技术效率和规模技术效率，表示为：

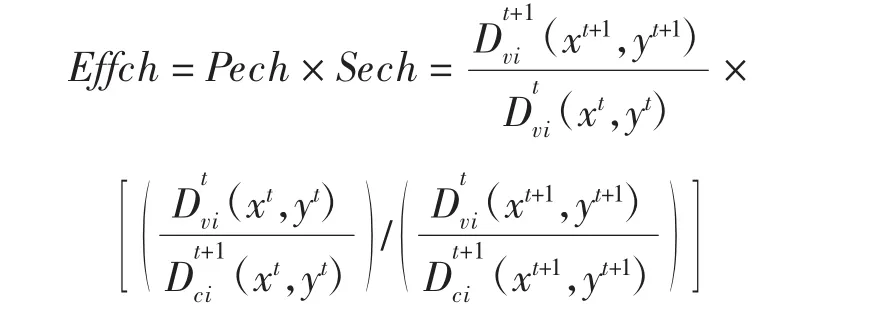
式中，Pech为决策单元在经营中获得的规模效应，当Pech〉1时，表示决策单元获得最优规模，反之则规模报酬不优。Sech为决策单元在技术水平变化时产生的效果，当Sech〉1时，表示决策单元技术进步或技术创新程度高，反之则技术进步或创新程度低。

2 数据来源及处理

采用Malmquist指数计算全要素生产率时，需要求得实际投入和产出变量的衡量指标。产出变量的衡量指标为国内生产总值；投入包含资本和劳动两个变量，衡量指标分别为资本存量和从业人员数。以国内31个省份作为决策单元，各变量衡量指标的数据来源及处理方法如下。

2.1 国内（地区）生产总值

国内生产总值即一定时期内生产出产品和劳务的价格总和，用GDP来表示。为了消除通货膨胀的影响，采用以2000年为基年的产品价格指数对货币GDP进行折算，得到实际GDP（以2000年的不变价格表示）。2000—2014年全国及各省份名义GDP来自《中国统计年鉴（2000—2014）》。

2.2 资本存量

关于资本存量的估算有多种方法，目前学界通常使用Goldsmith于1951年创造的永续盘存法。其估算式表示：Kt=Kt-1×（1- δ）＋ It/Pt，其中 Kt和 Kt-1分别表示第t和t-1期间的实际资本存量，It为第t期间的资本投资额，Pt为第t期间的价格指数，δ为t期间的折旧。资本存量的估算涉及以下数据：一是基期资本存量。基期资本存量可以采用两种方法确定：直接普查法和“折旧—贴现”法，目前学界主要采用“折旧—贴现”法。本文在借鉴张军和单豪杰方法的基础上，用固定资本形成总额除折旧率与固定资本形成总额增长率之和确定基期的资本存量[7-8]。二是固定资本投资。固定资本投资一般选用固定资产投资额进行估算。需要说明的是，官方统计网站中获取的固定资本投资额是没有考虑价格因素的名义值，需要用投资价格指数进行折算，得出实际的投资额。三是折旧率。折旧率的大小直接影响资本存量的准确度，本文采用余额折旧法计算。折旧率主要由边际替代率和资本品的寿命决定。边际替代率使用法定残值率替代，我国的法定残值率为0.003～0.005。由于资本品的使用寿命不同，已有文献对折旧率的计算存在差异。在官方公布的数据中，大部分将资本投资分为建筑和设备两大类，由于现代经济技术的快速发展，加之和已有文献进行比较，本文假设建筑及其设备的使用期限分别为35年和15年，资本品的残值率取5%，首先根据余额折旧法的公式算出折旧率分别为8.2%和18.1%，其次，计算这两类资本品在总固定资本中的平均比重，即建筑/设备与平均库存的和与资本形成额的比值，得出2000—2014年建筑和设备在固定总投资中的平均比重为70.67%和29.33%。最后，加权得出资本平均折旧率为11.10%。全国和省份固定资产原值、固定资产价格指数均来自《中国统计年鉴》《新中国统计资料55年汇编》《新中国统计资料60年汇编》、万得数据库等。

2.3 劳动投入

劳动力指标采用地区的就业人员数。2010年之前的数据来自《中国人口与就业统计年鉴》和《中国劳动统计年鉴》，2010年之后的数据来自各省统计年鉴。

3 实证结果和分析

本文以国内31个省份2000—2014年的全国投入产出数据为基础，在产出导向模型下，运用DEAP 2.1计量软件计算了全国及省份逐年Malmquist生产率指数及其分解指数，结果见表1。

从全国层面看，2000—2014年间，我国TFP的均值为1.002，即呈现出增长态势。TFP的年平均增长率为0.2%。根据分解的数据可知，技术效率的年均增长率为－0.5%，呈现负增长趋势，技术进步的年均增长率为0.7%，呈现增长趋势。技术效率的提升又取决于纯技术效率和规模效率，其中，纯技术效率和规模效率对经济增长的贡献均为负值。通过以上数据可得出：（1）在计算期内，我国的TFP虽然处于增长态势，但是效果不明显。技术进步和技术效率的增长率反方向变动，说明我国在技术引进与管理、制度等方面不匹配，造成全要素生产率的增长较低。（2）技术进步的提高消除了技术效率下降的影响，因此全要素生产率的增长主要依赖技术进步因素。（3）纯技术效率的变化指数和规模效率的变化指数在观察期均小于1，也是导致技术效率下降的主要原因。（4）2006—2007年TFP达到顶峰，2006年是我国自1997年以来经济增长最快的一年。（5）2008—2009年在金融危机的影响下，我国的TFP出现了下降的趋势。为了应对危机，2008年11月颁布了4万亿的投资计划以此扩大内需。2009—2010年我国经济增长率出现回升，但是回升还不牢固，发展方式还较为粗放，结构调整压力仍然较大，产能过剩严重，之后的各年经济增长率都没有达到峰值。

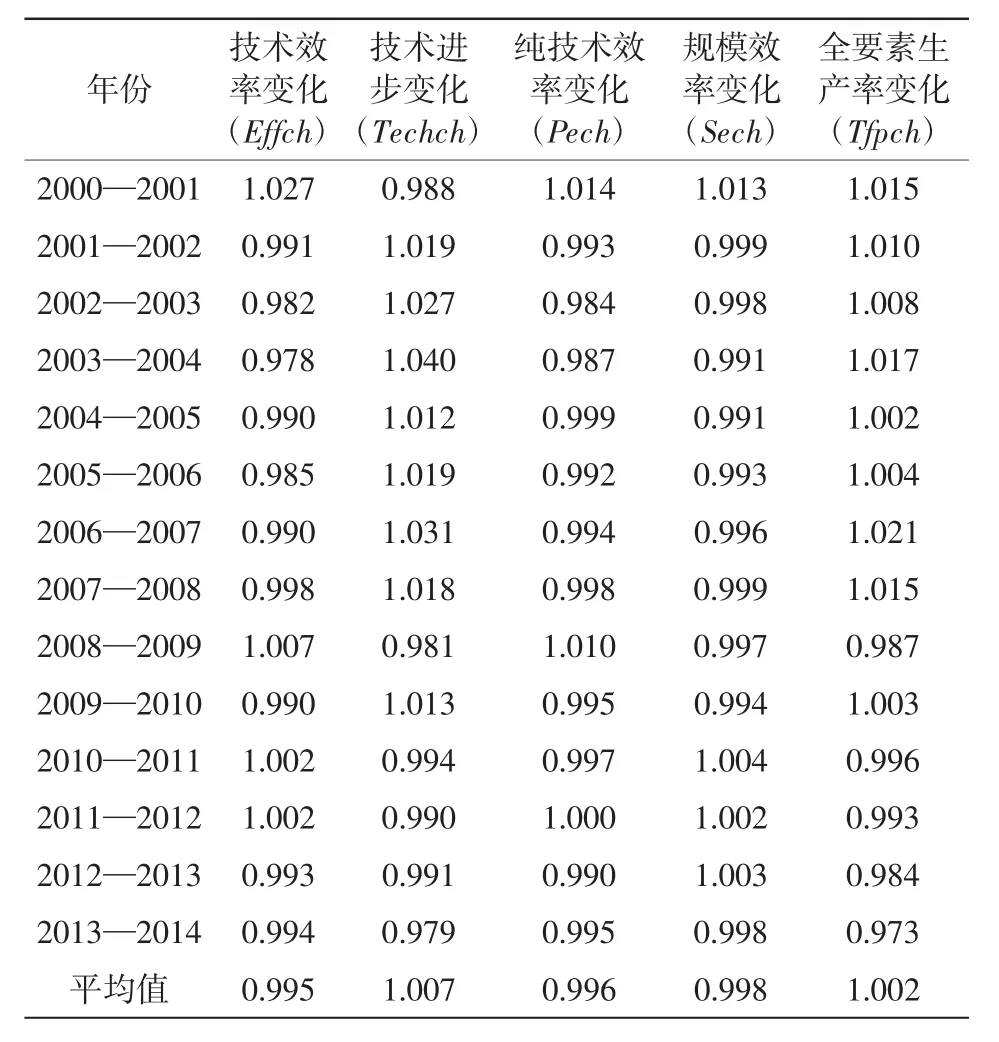
表1 2000—2014年全国的TFP值及其分解

从各省级地区层面看，2000—2014这15年间，TFP最高值为上海的1.044，最低值为广西的0.959，总体水平比较高，TFP出现正增长的省份有16个，占总数的51.6%。在技术进步方面，我们发现，上海的技术进步增长率最高，表明上海长期处在技术的前沿面，这主要与国家对科研投入的强度逐渐增加，科研力量在经济增长方面作用加大有关。除上海外，北京、辽宁、浙江、江苏、天津等东部地区的技术进步率也都大于1，其原因是，这些地区经济基础好，先进的技术引进和优秀科研人才率先流入这些区域，在经济增长中实现了技术创新和技术的最佳配置。在技术效率方面，全国17个省份处于负增长态势，且技术效率的下降是由纯技术效率和规模效率造成的。为了全面地研究TFP变化的地域差异，本文按照三大区域分析。

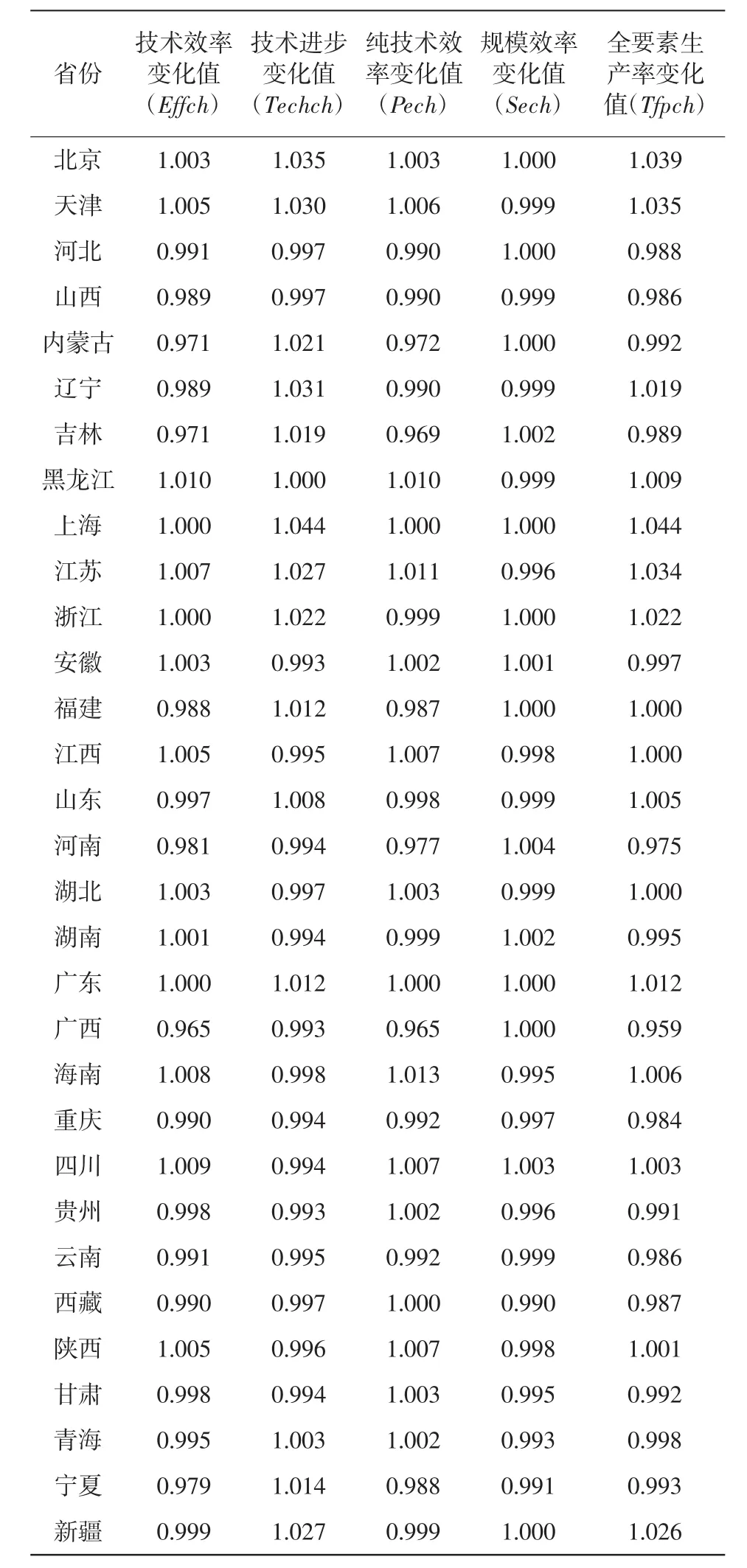
表2 2000—2014年各省级地区TFP值及其分解

从区域层面计算结果可知，东部、中部和西部区域的TFP差距较大，如图1所示。东部的TFP平均增长率为2%，中西部呈现负增长，分别为0.5%和0.3%。生产率的差异是造成三大区域间经济发展不平衡的主要动因。东部、中部和西部的技术进步均处于增长态势，处于技术前沿的是东部，年均技术进步增长率达到2.2%，可以看出东部地区TFP的增长主要取决于技术进步因素。而中部和西部地区的技术进步率呈下降态势，因此，地区间的技术落后也是造成区域之间经济差异的主要原因。

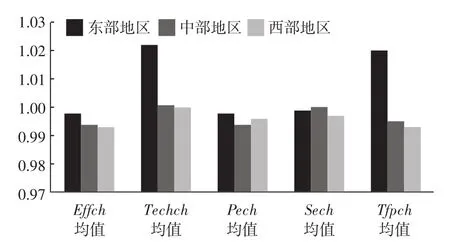
图1 2000—2014年三大区域的TFP值及其分解

三大区域的技术效率均为负值，其中东部均值为0.998，中、西部均值分别为0.994和0.993。区域间技术效率的普遍下降是由纯技术效率和规模经济造成的。东部和西部地区是由规模不经济造成的，因此东部和西部可以通过扩大生产规模实现经济增长。需要说明的是，西部地区较低的全要素生产率是由较低的技术效率作用的，由于西部资本、劳动等要素流动性差，不能及时调整。要改变西部地区的经济状况，就要调整区域产业结构、招商引资、提高管理水平、优化制度环境等措施改善技术效率环境，实现技术上的“后发优势”。

由图2可见：全国和东、中、西部全要素生产率处于波动状态且均下降，其中东部地区略有下降，中部和西部地区下降明显且波动趋势与全国基本保持一致。东部TFP的增长率水平高于全国平均值为2%，而中、西部TFP的增长率均低于全国水平，分别为－0.5%和－0.3%。图形和数据结果相吻合。

4 区域收敛性分析

由TFP的描述性统计分析可知，三大区域的TFP差异较大，具有显著的区域特征，但并不清楚TFP是发散还是收敛。因此，需要对三大区域TFP的变化做收敛性检验，考察区域差异的演变趋势。收敛性检验是考察TFP变动趋势的一种有效方法。在考察收敛性检验的文献中，收敛性分析方法主要有三种：σ收敛、绝对β收敛和条件β收敛。

4.1 收敛检验

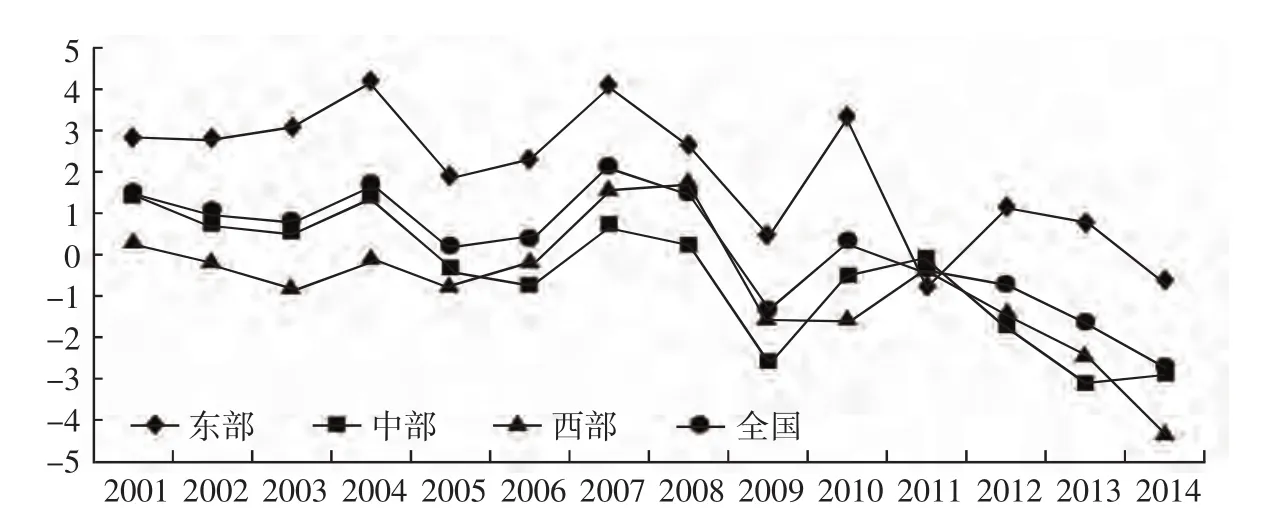
图2 TFP增长率区域差异及变化趋势

收敛一般用来分析地区间收入差距随时间的分布态势。TFP的标准差随着时间出现下降趋势，说明地区间收入趋同，收入差距缩小，即为σ收敛；标准差随着时间出现上升趋势，说明收入差距增大，即为σ发散。以往关于σ收敛的检验，通常使用多种指标进行增长差异的测度，如变异系数、赛尔系数、基尼系数等。由于方法和数据的差异，文献研究得出的结果并不相同。本文使用标准差来分析我国各地区间TFP的收敛态势。根据计算2001—2014年TFP的标准差，得出t时期的标准差图。

由图3可见，2001—2006年间，全国、东部、中部和西部的TFP标准差存在下降趋势，即都从最高点下降到一个稳态值，在2006年表现出明显的收敛态势。这说明，地区间收入差距逐渐缩小。从2007年开始，全国和三大区域出现发散态势，受到2008年全球金融危机的影响，区域间的全要素生产率增长率差距逐渐拉大，以东部最为明显，但发散的时间不一致。由于我国应对危机采取的有效措施，使得全要素生产率从2011年开始趋于收敛，且全国和三大区域表现出很强的时间同步性。同时，东部的TFP标准差较中部和西部略高，说明东部的内部差距比中部和西部明显，这可能是因为东部地区既有直辖市，又有普通省份的缘故。

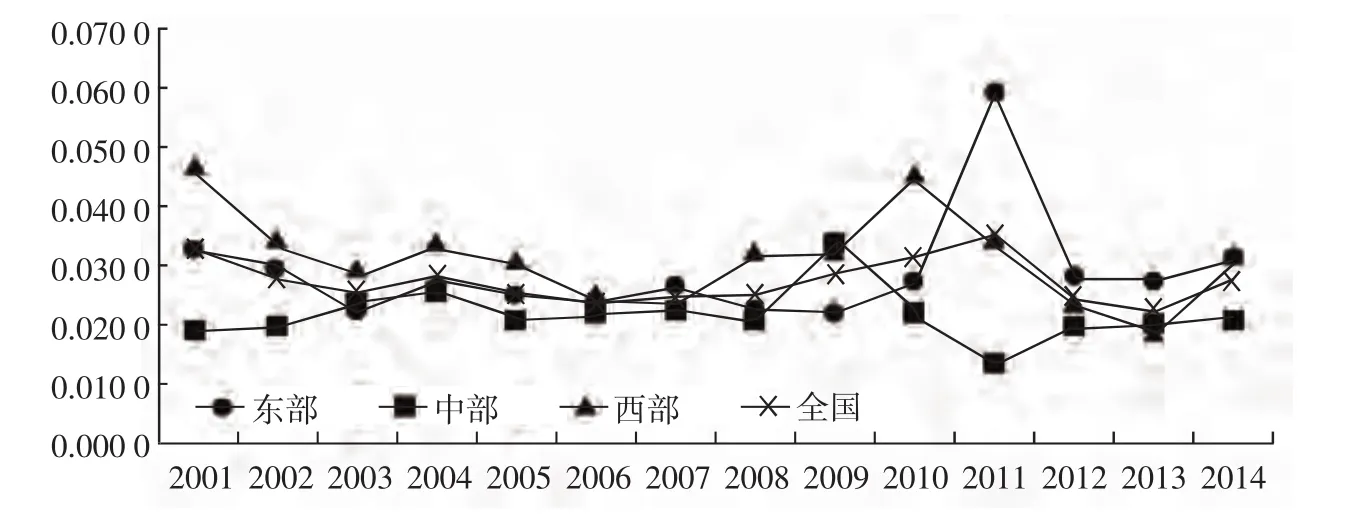
图3 全国及区域的TFP标准差图

4.2 β收敛检验

β收敛有绝对β收敛和条件β收敛之分。绝对β收敛主要探讨落后地区能否赶上发达地区；条件β收敛则用来验证各地区能否达到各自的收敛稳定水平。借鉴彭国华的研究思路[9]，绝对β收敛公式设定如下：

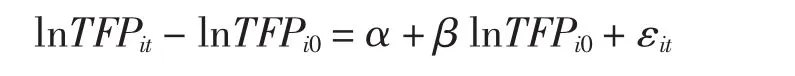
其中：it—i0从第0到第t期TFP的增长率，i0为第0期的TFP，εit为随机干扰项。若β为负值，说明存在收敛性；β为正值，说明存在发散性。

绝对收敛速度λ的计算公式为：

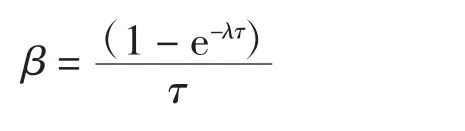
其中：λ为绝对收敛速度，τ为各年年份。

将计算得到的2000—2014年全要素生产率数据进行对数处理，根据绝对收敛检验模型，运用Eviews 7.0软件得出检验结果如表3所示。

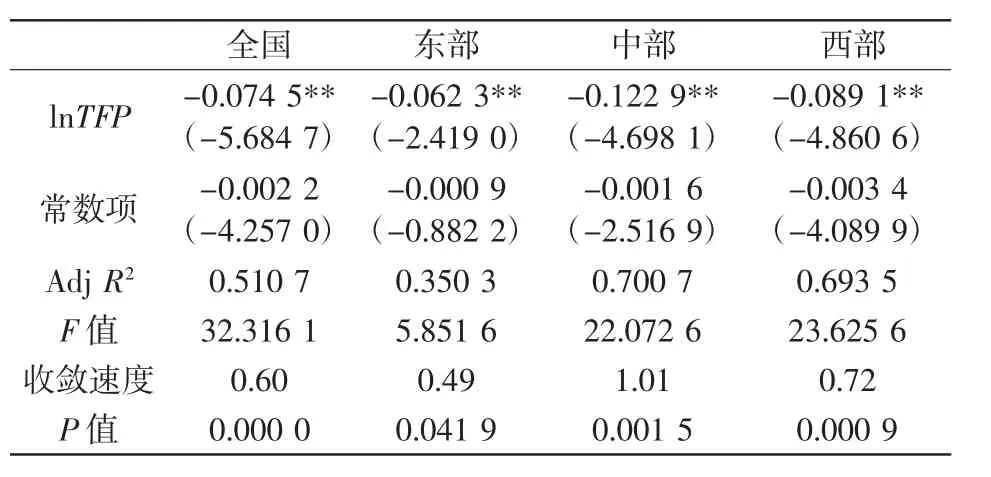
表3 我国TFP的绝对收敛，OLS的回归结果

表3报告了绝对收敛的OLS检验结果，从显著性值可知，全国TFP为负值，即呈收敛态势，且TFP之间的差异以0.6%的收敛速度缩小。分区域结果显示，东部地区绝对β收敛系数为－0.074 5，中部地区为－0.122 9，西部地区为－0.089 1，均呈收敛状态。其中，收敛速度为中、西、东依次递减。这一结果的原因可能是中部地区和西部地区近年来经济发展加速，通过学习东部地区先进的科技和管理方式，使得区域间的差距缩小，实现了“追赶效应”。东部地区的收敛速度最慢，结合前面的σ收敛可知，东部地区存在“俱乐部效应”。

测度条件β收敛检验主要有两种方法，一种是运用索洛增长模型并加入控制变量，如折旧率、储蓄率等估算；另一种是运用面板固定效应模型估算方法，它的优点是既考虑了个体间稳态值的差异，又考虑了不同稳态值随时间变化的趋势。为了获得稳健的研究结果，本文采用各省份面板数据分别检验了混合最小二乘法、固定效应和随机效应模型；通过F和Hausman检验，选择使用面板数据的固定效应来分析条件β收敛。

条件收敛检验具体模型如下：

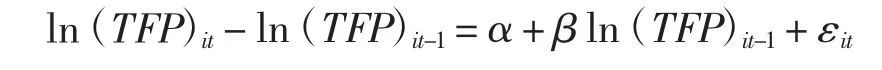
其中：ln（TFP）it-ln（TFP）it-1为差分过程，i为省份，t为年份，εit表为随机干扰项。若β为负值，说明存在收敛性；β为正值，说明存在发散性。

条件收敛速度的计算公式：

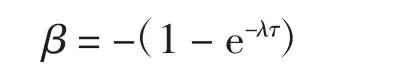
其中：λ为条件收敛速度，τ为各年年份。

利用上述模型，根据2001—2014年全国和各省份全要素生产率增长率数据，运用Eviews 7.0软件，得到回归结果如下：

由表4的结果可知，所有的β为负值且均通过了1%的显著性，从整体来看，全国的TFP随时间存在条件β收敛且向自身的稳定方向发展，且收敛速度为0.48。分区域看，东、中、西部由于经济发展的环境不同，TFP均收敛于各自的稳定水平。其收敛速度顺次为东部地区、全国、中部地区和西部地区。

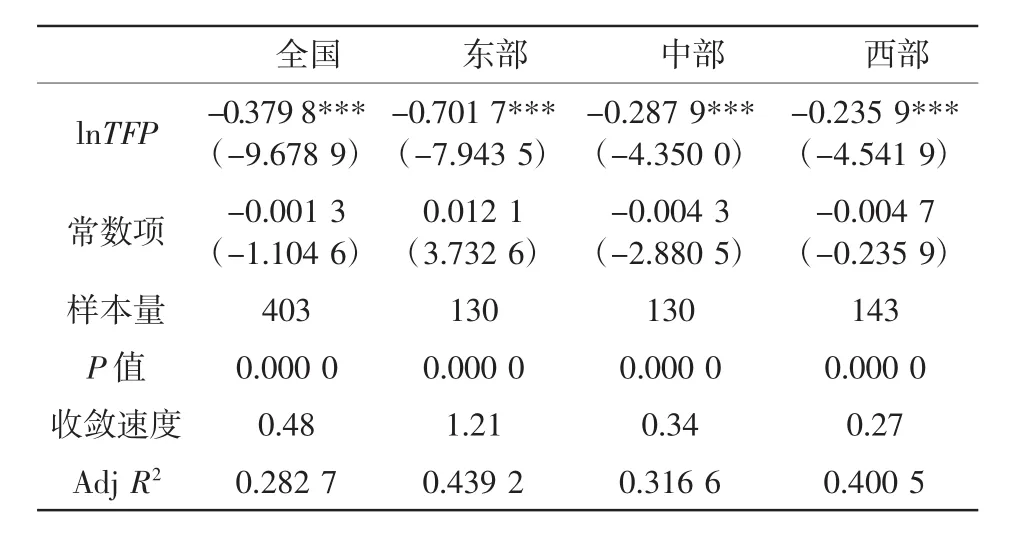
表4 我国TFP的条件收敛，固定效应的回归结果

5 结论和政策启示

本文基于非参数前沿分析方法，通过总产出、劳动投入量和资本存量数据，测算了2000—2014年全国及东、中、西三大区域全要素生产率的增长率；并分析了2001—2004年TFP的收敛情况。结论如下：

第一，2000—2014年，中国TFP的增长效果并不明显。技术进步的提高消除了技术效率下降的影响，因此全要素生产率的增长主要依赖技术进步因素。纯技术效率和规模技术效率均呈负增长趋势，也直接导致了技术效率的降低。

第二，东部、中部和西部TFP增长率之间存在差距，但其变化趋势与全国基本保持一致。东部的TFP增长率较全国水平略高，中部和西部较全国水平略低。东部TFP高增长的源泉为技术进步；中部和西部TFP低增长的原因来自于较低的纯技术效率和规模效率。

第三，由σ收敛性检验可知，全国和各区域TFP标准差存在波动下降趋势，即都从最高点下降到一个稳态值又出现震荡到一个稳态值，说明区域间经济体的差异逐渐缩小。由绝对β收敛检验可知，全国整体而言TFP是收敛的，且差异逐渐缩小。分区域而言，东部、中部和西部地区的TFP均呈收敛态势；并且，中部地区的收敛性最强，西部地区次之；而东部存在较强的“俱乐部效应”。全国整体的全要素生产率随时间存在条件β收敛且向自身的稳定方向发展；东、中、西部地区则存在各自稳态，且向各自稳态水平收敛的态势。

上述结论的政策启示为：为继续促进经济的可持续发展，推动经济增长方式的集约化转变，应加大提升各地区全要素生产率的力度；同时，中央和地方政府制定技术进步推动政策的过程中，要更加关注技术效率的改善措施，使技术进步和技术效率趋同发展。另外，中部地区和西部地区的全要素生产率依然很低；为降低“马太效应”，中央政府应继续加大对中西部地区的扶持力度；各地区应制定符合本地区禀赋条件的政策以缩小与发达地区的差距。

［1］ 王志平.生产效率的区域特征与生产率增长的分解——基于主成分分析与随机前沿超越对数生产函数的方法［J］.数量经济技术经济研究，2010（1）：33-43.

［2］ 郭庆旺，贾俊雪.中国全要素生产率的估算：1979—2014年［J］.经济研究，2005（6）：51-60.

［3］ 张煜，孙慧.基于DEA的Malmquist指数法的省域全要素生产率比较研究［J］.干旱区地理，2016（3）：436-442.

［4］ 刘建国，李国平，张军涛，等.中国经济效率和全要素生产率的空间分异及其影响［J］.地理学报，2012（8）：1069-1084.

［5］ 颜鹏飞，王兵.技术效率，技术进步与生产率增长：基于DEA的实证分析［J］.经济研究，2004（12）：55-65.

［6］ CAVES DW，CHRISTENSENL R，DIEWERT W E.The economic theory of index numbers and the measurement of input，output，and productivity［J］.Econometrica，1982，50（6）：1393-1414.

［7］ 张军，章元.对中国资本存量K的再估计［J］.经济研究，2003（7）：35-43.

［8］ 单豪杰.中国资本存量K的再估算：1952—2006年［J］.数量经济技术经济研究，2008（10）：17-31.

［9］ 彭国华.中国地区收入差距、全要素生产率及其收敛性分析［J］.经济研究，2005（9）：19-28.