基于最大贡献的航班计划优化模型

冯辉宇，武丁杰，罗 超

(中国民用航空飞行学院 空中交通管理学院，四川 广汉 618307)

为了提升航空公司的市场竞争力，其生产运营效率是至关重要的。生产运营效率可以在很多方面得到体现，例如完善的机队维修计划、机组的配备以及航班计划等。航班计划是一切生产运营活动的基础，也是后续服务的保障。本文将从航班计划优化的角度探讨如何提高航空公司的收益及生产运营效率。

1 航班计划优化模型

1.1 问题分析

一般来说，航班计划的优化是以利润最大化为基础的。本文从航班贡献的角度去研究航班计划的优化问题。航班贡献的多少可以反映出一个航空公司整体的盈利情况[1]。航班贡献小于0，则飞行越多，亏损越多。航班贡献大于0，即使利润为负，由于航班收入可以覆盖变动成本及附加税，航班飞行之后，可以分摊一些固定成本。为了开辟市场，这样的航班仍可继续运行[2]。

1.2 模型假设及符号说明

1.2.1 模型假设

(1)航班的飞行频率即每天飞行的航班架次已经确定；

(2)航空公司的机队规模已经确定，短时间内不会有很大的变化；

(3)不考虑机型，这里我们定义最小过站时间为45 min；

(4)航线网络已经确定，航班会按既定的航线飞行；

(5)客运和货运流量根据历史数据已经预测。

1.2.2 常用符号说明

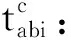
1.2.3 模型的建立

本文主要从航班收入、航班成本、航班贡献这三方面考虑来建立模型。航班的收入主要以座公里收入及客座率来体现，座公里收入是民航领域的最终评估指标，既可以用来对比单个航班的经营品质优劣，也可以用来对比整条航线的优劣。航班的成本主要由2部分组成，即固定运输成本和变动运输成本。固定运输成本在上述中讲过，在一定时期内是不变的。变动运输成本与航班的运行情况有关，一般与航班的客运和货运量相关，客运、货运量的提升都会使航班的变动运输成本增加。

建立一个以航班总贡献最大的航班计划模型：

(1)

上式中，用W表示航班的总贡献，它由收入、成本、附加税计算所得，其中的kij·dik·sij·yij表示单个航班的收入，k表示该航班的座公里收入，它是衡量航班运营情况的一个重要指标。d表示航班飞行的航线距离，该值主要以民航局公布的航段距离为主，不考虑实际航班飞了多长。s表示执飞该航班飞机的座位数，以官网公布的数据为准，由于存在改装，各个航空公司同一种机型的座位数略微存在差异。y表示客座率，它可以很好的反应航班的销售情况。变动运输成本主要体现在客运和货运两方面，它们是影响变动运输成本最主要的两个因素，这里我们用一个线性函数βij+Lijbij+Kijeij表示变动运输成本。其中βij表示机型j在航线i上的空载情况下的变动运输成本，bij和eij分别表示机型j在航班i上的客运和货运的空载和满载情况下所需变动运输成本的差值，Lij和Kij分别是与之对应的一个系数。λij表示的是一个0-1变量：

此外，根据研究，民建基金为运输收入的5%，营业税金及附加为运输收入的3.75%[3]。

建立的模型满足以下约束条件：

(2)

(3)

(4)

(5)

(6)

(7)

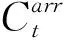
2 模型求解算法

由于上述模型属于NP问题，现代优化方法中精确算法是解决小规模问题的求解方法，针对这种大规模问题的求解，常采用启发式算法或者说近似算法。由于传统的遗传算法收敛过快，禁忌搜索算法只能求得局部最优，为了克服这一缺点，本文采用引入禁忌搜索的遗传算法，将禁忌算法的“禁忌”和“特赦”准则引入到遗传算法中，克服遗传算法早熟的现象，求得全局最优解[6]。这种思想主要表现在遗传算法的交叉算子上，通过改进后的交叉算子我们将其称为TSR算子。

2.1 遗传-禁忌混合算法

(1)编码。一般遗传算法在处理问题空间的参数时有一定难度，需要用一定的方式将其翻译成遗传算法可识别的参数，这里我们采用有序串编码的方式来实现这一过程。对于上述n个航班的优化问题，我们将染色体分为n段，这样，每一段就对应着航班的编号。例如待优化的航班有6个，那么|5|6|1|3|2|4就可以表示是一个可行的染色体。

(2)种群初始化。编码之后就是种群的初始化，在此之前，需要确定初始化种群的数量，初始化种群的数量一般根据经验得到，本文中种群的数量可以根据航班规模的大小确定。确定初始种群数量之后，选择其中一个作为初始解。

(3)适应度评价。适应度是用来区分群体中个体优劣的标准，是对种群染色体筛选的一个依据。适应度值需要根据实际情况选取，优化的目标就是尽可能寻找适应度值大的染色体，选取的染色体适应度值越大，优化的结果就越好。

(4)选择。选择操作就是以一定的概率将旧群体中的个体选择到一个新的群体中，适应度值的大小影响个体被选取的几率，适应度值越大的个体往往被选取的几率就越大。本文中，选择算子我们选择子轮盘赌法的方式，个体i被选中的概率为

(8)

其中，Ki为个体i的适应度值。

(5)TSR算子。将禁忌搜索算法的禁忌和特赦准则运用到遗传算法中的交叉操作上，它是基于一种优胜劣汰的方法，将较好的染色体直接保留到下一代中，减少了个体被替换的次数，优化了算法的速度。在交叉操作产生的子代中，如果子代足够优秀，已经达到渴望水平，那么无论其是否被禁忌，它都可以直接进入到下一代。如果产生的子代不是很优秀，未达到所需的渴望水平，那么需要考虑其是否被禁忌了。如果没有被禁忌，就可以保留到下一代；如果被禁忌的话，我们选择保留父代中优秀的染色体进入到下一代中，子代被淘汰。

(6)变异。为了使物种呈现多样化的特征，需要进行变异操作，随机选择种群中的个体进行变异操作，以产生更加优异的个体。第i个个体的第j个基因gij进行变异的操作方法为

(9)

其中，gmax表示基因gij的上限，gmin表示基因gij的下限；f(g)=r2(1-g/Gmax)2,其中的r2是一个随机数，g是当前迭代次数，Gmax是最大进化次数，r表示[0,1]区间的随机数。

2.2 算法步骤

主要步骤如下：

步骤1 编码，初始化群体，给出算法的初始参数，主要包括群体规模、最大迭代次数、交换概率等信息；

步骤2 计算各个个体的适应度值；

步骤3 利用选择算子进行选择；

步骤4 利用TSR算子进行交叉操作，具体操作方法如下：

(1)对于每一个染色体，随机生成一个数，如果这个数大于交叉概率，那么这个染色体被选中，否则没有被选中；

(2)被选中的染色体为父代染色体，对父代染色体进行交叉操作，以产生两个后代染色体；

(3)渴望水平由父代适应度的均值确定，禁忌对象为群体中染色体的适应度值；

(4)若子代染色体的适应度值大于预先设定的渴望水平，则不考虑其是否被禁忌的情况，直接将子代染色体保留到下一代中；若没达到渴望水平，则进行下一步操作；

(5)对于没有达到渴望水平的子代染色体，如果其没有被禁忌，也可以将其保留到下一代中，并更新禁忌表，如果未达到渴望水平同时也被禁忌的话，则将其全部淘汰，选择父代染色体中优秀的部分保留到下一代中；

步骤5 进行变异操作；

步骤6 判断筛选结果是否满足终止条件，如果满足，直接输出结果，如果它不符合，返回到步骤(2)。

3 案例分析

以某航空公司南京禄口机场为枢纽的航班为例，2016年11月份部分航班销售情况如表1所示。

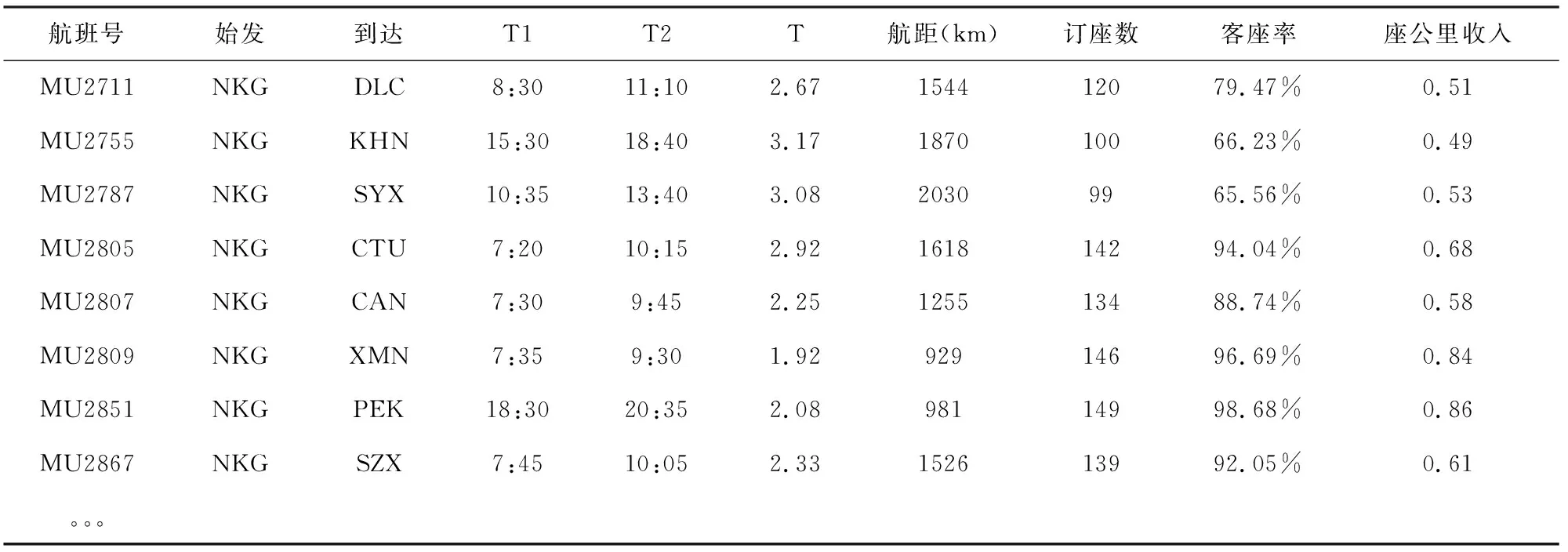
表1 部分航班销售情况

注：T1为航班的起飞时间；T2为航班的到达时间；T为航班的飞行时间，单位为h(小时)。

航班的变动运输成本主要有飞行小时费、航空油耗消耗、航材消耗件消耗、起降服务费、航食及供应品费、代理业务手续费、基建和税金等。确定了机型、航段，飞行小时、单位小时油耗、航材消耗件消耗单位值、起降费用及航路费都可以确定。航食及供应品随旅客的变化而变化，该航空公司的飞机大多是客货混装的，由于货邮需求不是很大，为了简化模型，在模型中就不考虑货邮的变动运输成本。

通过Matlab软件仿真，设定种群规模为30,最大遗传代数为300,变异概率为0.2,对比寻优分析模拟结果如图1所示。

图1 对比寻优分析模拟结果

从图中我们可以看出，相比传统的遗传算法，遗传禁忌混合算法求得的结果更优，且进化代数也较小。由于选取部分航班数据，两种算法之间的差距不是很明显。但随着数据的增多，数据复杂程度增加，遗传混合算法的优越性会更加明显。

4 结语

本文通过对航空公司经营效率和航班计划的分析，以航班贡献为切入点，研究航空公司整体的盈利情况。从航班收入、航班成本以及航班贡献三者之间的关系出发，建立了以航班贡献为目标的优化模型，该模型可以很好的反映出航班运营情况对航班贡献的影响。采用遗传和禁忌的混合算法对模型求解，把禁忌算法的禁忌和特赦准则引入到遗传算法中，缓和遗传算法收敛过快的现象，从而提高最终的优化结果。

[1] 程望斌，冯彩英，曾毅，等.航班计划的优化设计研究[J].湖南理工学院学报(自然科学版)，2016，29(2):38-42，88.

[2] 上官雪民. 航班计划的模拟与优化研究[D].上海：复旦大学，2008.

[3] 张伯生，刘飞.实现航班计划优化的动态规划模型[J].上海工程技术大学学报，2004，18(2):135-140.

[4] 黄小荣. 航班收益分析与最佳航班安排[J].中国民航学院学报(综合版),2001，19(6):19-22，26.

[5] 杨新湦，齐莉，翟文鹏.航班时刻资源优化配置与延误水平评估[J].河南科技大学学报(自然科学版)，2016，37(3):19-23，5.

[6] 李大卫，王莉，王梦光.遗传算法与禁忌搜索算法的混合策略[J].系统工程学报，1998，13(3):28-34.