人工骨3D打印与铣削复合加工研究*

刘 徽 杨先海 程 祥 吕福顺 王 飞 孙秋莲

(山东理工大学机械工程学院，山东 淄博 255000)

现阶段我国人口老龄化现象越来越严重，另外，疾病与交通事故等客观原因导致了身体骨骼的病变或缺失，人工骨的需求越来越多。部分学者将仿生人工骨作为替代人骨的材料，并在很大程度上解决了骨来源紧缺及疾病传播问题[1]。制造人工骨的材料多种多样，其中特种工程塑料PEEK以其优异的耐磨性、生物相容性、化学稳定性等优点成为目前最具应用前景的人工骨基体复合材料，可独立作为人工骨替换材料使用[2]。此外，不同人的骨骼在结构、形态等方面千变万化，需要人工骨的个性化定制。3D打印技术在个性化复杂结构快速制造方面的优势正好满足了这些需求[3]。因此，有必要对3D打印在人工骨制造方面的应用作进一步的研究。

夏琰等人以无机的羟基磷灰石与有机的聚己内酯作为原材料，使用3D打印技术中的选择性激光烧结技术(SLS)制备出组织工程化纳米-羟基磷灰石/聚己内酯人工骨支架[4]，为其今后在骨缺损治疗中的应用奠定了一定的试验基础。张永强等人针对人工骨的需求问题,结合CAD、熔融沉积3D打印技术, 以PHA/β-TCP复合材料制备出具有三维多孔结构的人工骨支架[5]。张钰等人在对3D打印样件进行热力学仿真和试验研究的基础上，利用自行开发的3D打印装置在最优打印条件下成功制造出PEEK仿生人工骨，突破了其只能用注塑和激光烧结制造的局限，具有理论和实际应用价值[2，6]。利用熔融沉积成型(FDM)原理进行聚醚醚酮(PEEK)仿生人工骨的3D打印制造是一项新的技术，目前尚处于起步阶段。

然而，FDM打印出的制件表面质量较差，与医用要求有一定的差距。铣削加工是公认的高质量、复杂几何特征加工的工艺[7]。鉴于此，本文应用自主研发的熔融增材与铣削减材复合加工机床，针对PEEK材料人工骨，展开3D打印与铣削复合的加工研究。其中FDM技术中打印时间、打印材料消耗量是已经被普遍关注的研究对象，但对打印试件的力学性能研究较少。故本研究针对3D打印，选取打印时间、打印材料消耗量、试件的储能模量为响应值，针对铣削，选取加工铣削后试件表面的粗糙度为响应值，构建数学模型，优化3D打印与铣削工艺参数。并进行试验验证。

1 试验准备

1.1 试验方法

响应面法是一种综合试验设计和数学建模的优化方法，通过对具有代表性的局部各点进行试验，回归拟合全局范围内因素与结果间的函数关系，并且取得各因素最优水平值。其中，Box-Benhnken Design(BBD)法是一种采用试验设计理论对指定的设计点集合进行试验得到目标函数和约束函数的响应面模型，来预测非试验点的响应值的方法[8-10]。应用此方法时使用的软件为Design-Expert。本文将响应面法用于3D打印与铣削的工艺参数优化中，为了提高研究效率，本文采用简单形状试件的打印与铣削加工，将试件的形状设定为长方体。

1.2 3D打印与铣削试验因素水平

参考前期研究[11-12]，选取对打印时间、打印材料消耗量、储能模量影响较大的层厚、内部填充密度、外周轮廓为因素。各因素水平见表1。

表1 打印试验因素水平列表

因素水平 层厚/mm内部填充密度/(%)外周轮廓/圈10.230220.350430.4706

基于前期研究，确定背吃刀量、主轴转速、进给量的三因素试验，各因素水平见表2 。

表2 铣削试验因素水平列表

因素水平 背吃刀量/mm主轴转速/(r/min)进给量/mm10.23 0000.0620.43 5000.0930.64 0000.12

1.3 试验设备

本试验进行3D打印与铣削所用设备为自主研发的熔融增材与铣削减材复合加工机床[7]，如图1所示。试验采用孔径为0.5 mm的喷嘴，打印温度为365 ℃，底板温度180 ℃，打印速度15 mm/s，打印内部填充形式选为直线型。选用的端铣刀参数：刀具直径3 mm，齿数3齿，螺旋角30°，材料为硬质合金。

测量储能模量的动态热机械测试仪型号为DMA-Q800。测试条件为：单悬臂测试方式，快速平衡至0 ℃，平衡时间5 min，以5 ℃/min的升温速率由0 ℃升至220 ℃。

铣削后试件表面的粗糙度由CS3200表面粗糙度测量仪测量。测量仪主要技术参数：抽样长度L=0.8 mm；评定长度5L；量程：±40 μm；精确度±10%；驱动速度0.5 mm/s，测力为4 m·N，工作环境为室温。测量粗糙度时，在几个均匀分布的位置上分别测量，每组试验至少测3次取平均值。

2 3D打印与铣削试验

2.1 试验步骤

打印长34 mm宽12 mm高3 mm的长方体，如图2所示。打印时间与打印材料长度由控制系统记录，根据材料长度计算出打印材料消耗量。对打印试件进行铣削试验，为节省试验所用材料，同一试件上进行3次铣削试验，单个试件铣削结束后效果如图3。

2.2 试验结果

打印试验与铣削试验响应面方案测量结果见表3和表4。表3中因素A为层厚，因素B为内部填充密度，因素C为外周轮廓；响应值R1为打印时间，响应值R2为打印材料消耗量，响应值R3为储能模量。表4中因素D为背吃刀量，因素E为主轴转速，因素F为进给量；响应值R4为粗糙度。

表3 打印试验测试结果

序号影响因素响应值A/mmB/(%)C/圈R1/sR2/cm3R3/MPa10.45065161 123.041 847.620.33024811 097.531 510.6930.35045661 189.21 325.5840.25068221 227.781 743.8450.37066331 233.961 473.3160.35045691 197.351 315.5870.25026301 265.81 545.0980.43044671 034.081 602.4690.37025301 237.511 341.7100.45024321 010.711 621.93110.23047051 208.451 663.64120.33066121 193.331 800.51130.27047371 296.171 276.57140.35045701 190.71 319.58150.35045671 197.31 333.58160.35045701 1901 322.58170.47044911 112.721 473.35

3 试验结果分析

打印时间的显著性分析结果见表5。显著性分析表中若某因素的P值小于0.01，表明此因素对响应值有极显著影响；若P值大于0.01小于0.05，表明此因素对响应值有显著影响；若P值大于0.05，表明此因素对响应值无显著影响。由表5可知：因素A层厚、因素B内部填充密度、因素C外周轮廓对打印时间的影响是极显著的；因素A的二次方A2对打印时间有极显著影响，而因素B的二次方B2和因素C的二次方C2对打印时间没有显著影响；交互项AC对打印时间有极显著影响，而交互项AB、BC对打印时间没有显著影响。相同的，打印材料消耗量、储能模量、铣削面粗糙度的显著性分析结果见表6～8。

表4 铣削试验测试结果

序号影响因素D /mmE /(r/min)F /mmR4 /μm10.24 0000.091.4220.43 5000.091.7730.23 5000.061.3340.63 5000.061.7250.64 0000.091.8160.44 0000.061.3570.43 0000.061.7480.44 0000.121.8790.43 5000.091.75100.63 0000.092.31110.43 5000.091.76120.23 5000.121.79130.23 0000.091.76140.43 5000.091.79150.43 5000.091.77160.43 0000.122.32170.63 5000.122.27

经回归拟合后，层厚、内部填充密度、外周轮廓三试验因子对响应值打印时间、打印材料消耗量、储能模量的影响可用回归方程表示为式(1)～(3)：

R1=841.7-2 673.0A+2.3B+85.5C-1.0AB-135.0AC-0.2BC-3 380.0A2-5.5×10-3B2-0.5C2

(1)

R2=1 103.9+322.1A+4.3B-6.6C-1.1AB+187.9AC-0.6BC+3 190.3A2+0.1B2+49.2C2

(2)

R3=4 018.2-11 512.2A-14.9B-301.6C+32.2AB+33.6AC-1.0BC+16 934.4A2+0.1B2+49.2C2

(3)

表5 打印时间模型的显著性分析表

方差来源自由度均方F值P值显著性Model918 272.76415.02< 0.000 1极显著A11.22×10-52771.34< 0.000 1极显著B11 984.545.070.000 3极显著C132 512.5738.44< 0.000 1极显著AB1160.360.565 6不显著AC12 91666.23< 0.000 1极显著BC11964.450.072 8不显著A214 810.27109.25< 0.000 1极显著B2120.380.460.518 2不显著C2120.380.460.518 2不显著失拟项398.33残差744.03总值161.6×10-6方差R297.12%

表6 打印材料消耗量模型的显著性分析表

方差来源自由度均方F值P值显著性Model910 607.07561.56< 0.000 1极显著A164 377.693 408.28< 0.000 1极显著B115 048.52796.70< 0.000 1极显著C13 467.78183.59< 0.000 1极显著AB120.611.090.330 9不显著AC15 651.28299.19< 0.000 1极显著BC12 467.61130.64< 0.000 1极显著A214 285.35226.87< 0.000 1极显著B2114.370.760.412 0不显著C2173.393.890.089 3不显著失拟项322.04残差718.89总值165 974.74方差R298.97%

经回归拟合后，背吃刀量、主轴转速、进给量三试验因子对响应值粗糙度的影响可用回归方程表示为式(4)：

R4=3.7+2.0D-1.6×10-3E+10.3F-0.4×10-4DE+3.8DF-1.0×10-3EF+0.2D2+2.0×10-7E2+2.5F2

(4)

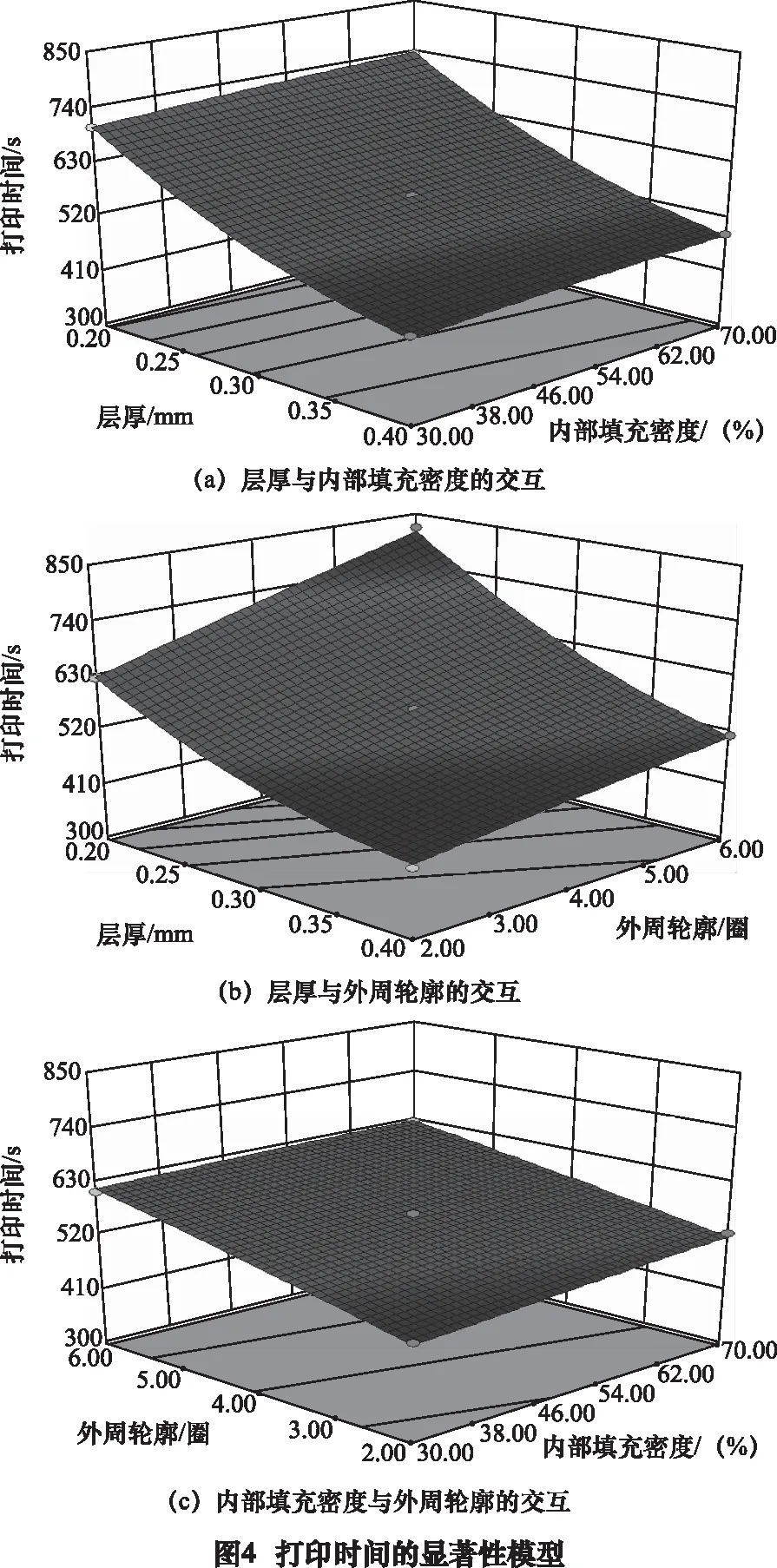
根据式(1)的回归模型作出AB、AC、BC交互作用等高曲线和响应曲面图，如图4所示。

表7 储能模量模型的显著性分析表

方差来源自由度均方F值P值显著性Model961 881.50885.84< 0.000 1极显著A112 497.81885.84< 0.000 1极显著B11.281×1051 833.94< 0.000 1极显著C189 432.781 280.24< 0.000 1极显著AB116 635.84238.14< 0.000 1极显著AC1181.172.590.151 3不显著BC16 257.6089.58< 0.000 1极显著A211.207×1051 728.50< 0.000 1极显著B21535.867.670.027 7显著C211.632×1052 336.60< 0.000 1极显著失拟项322.04残差718.89总值165 974.74方差R298.08%

表8 粗糙度模型的显著性分析表

方差来源自由度均方F值P值显著性Model90.15415.78< 0.000 1极显著D10.411 144.35< 0.000 1极显著E10.35985.87< 0.000 1极显著F10.561 555.12< 0.000 1极显著DE16.400×10-317.880.003 9极显著DF12.025×10-35.660.049 0显著EF19.000×10-42.510.156 8不显著D212.213×10-40.620.457 4不显著E210.01029.120.001 0极显著F212.132×10-50.0600.814 2不显著失拟项35.417×10-4残差73.579×10-4总值160.084方差R297.96%

由三因素交互作用对打印时间模型显著性分析可以得出，随着层厚的增大，打印时间呈减小的趋势；随着内部填充密度的增大，打印时间呈增大的趋势；随着外周轮廓数的增大，打印时间呈增大趋势。原因为层厚的增大导致层数的减少，这使得喷嘴走过的路径减少，因此打印时间减少。内部填充密度与外周轮廓的增大都会导致喷嘴走过路径的增加，所以打印时间会增加。

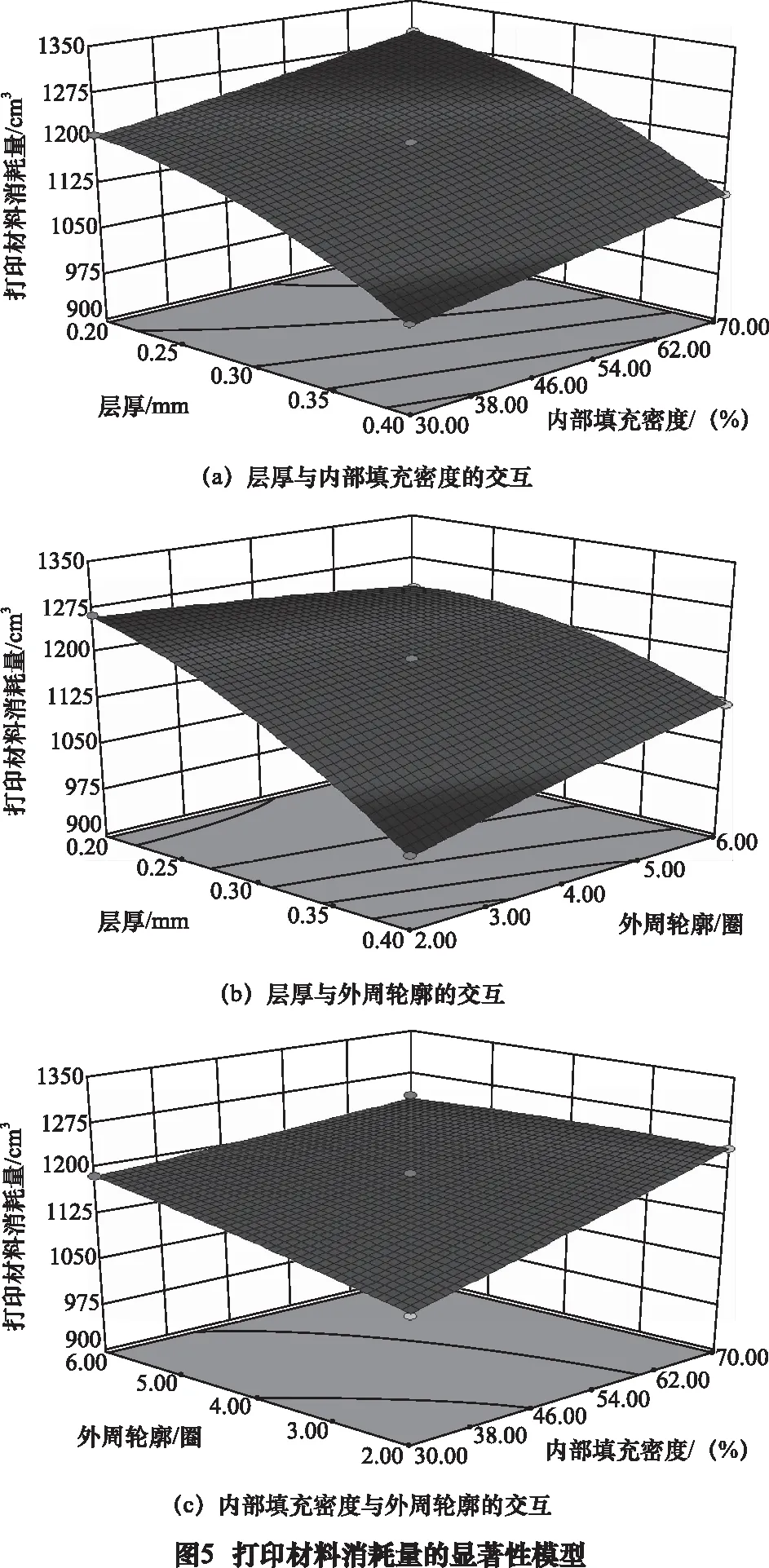
同样地，根据式(2)、(3)的回归模型作出AB、AC、BC交互作用等高曲线和响应曲面图，如图5、6所示。

由三因素交互作用对打印材料消耗量模型显著性分析可以得出，随着层厚的增大，打印材料消耗量呈减小的趋势；随着内部填充密度的增大，打印材料消耗量呈增大的趋势；随着外周轮廓数的增大，打印材料消耗量呈增大趋势。原因为层厚增大，层间间隙增大，因此打印材料消耗量减小。内部填充密度越大，需要越多的打印材料，打印材料消耗量增加。同层外周轮廓间隙为零，因此可将同一层的外周轮廓区域理解为填充密度为百分之百的区域，外周轮廓数的增加相当于整个试件的填充密度的增加，因此打印材料消耗量增加。

由三因素交互作用对储能模量模型显著性分析可以得出，随着层厚的增大，储能模量呈先减小后增大的趋势。这是因为层厚在刚开始增大时层数减少，而层间粘结力较小导致试件储能模量的减小。但层厚继续增大时层数减小较多，层间粘结力的影响变小，单层厚度增加，储能模量再次增加。随着内部填充密度的增大，储能模量呈减小的趋势。这是由FDM型3D打印的局限性所致，机床在打印内部填充密度较小的一层后会接着打印一层填充密度为百分之百的中间层。当内部填充密度较小时，后面打印的中间层会沉积到本层的空隙处使本层更为密实，所以会出现内部填充密度较小的试件储能模量反而大的情况。随着外周轮廓数的增大，储能模量先减小后增大，这是由于外周轮廓所占面积与内部填充面积冲突，受交互作用的影响，在外周轮廓数量刚开始变大时内部填充区域所发挥的作用减小，试件的储能模量减小，但随着外周轮廓数的增大，外周轮廓区域所发挥的作用变大，储能模量再次增大，所以储能模量在整个过程呈先减小后增大的趋势。

根据式(4)的回归模型作出DE、DF、EF交互作用等高曲线和响应面图如图7所示。

由三因素交互作用对粗糙度模型显著性分析可以得出，随着背吃刀量的增大，粗糙度值呈增大的趋势，粗糙度主要受铣削力的影响，铣削力随着背吃刀量的增大单调增大，因此粗糙度值也呈现单调增大的趋势。随着主轴转速的增大，粗糙度值呈减小的趋势；随着进给量增大，粗糙度值呈增大的趋势。

4 工艺参数优化及复合加工验证

4.1 工艺参数的优化

以3D打印时间最小、打印材料消耗量最小、储能模量最大为目标，对式(1)、(2)、(3)三个回归模型对所选取因素进行优化，得出3D打印工艺参数的最优组合为层厚0.43 mm，内部填充密度55.05%，外周轮廓1.39圈。

以粗糙度值最小为目标，应用式(4)的回归模型对所选取因素进行优化，得出铣削工艺参数的最优组合为背吃刀量0.2 mm，主轴转速3 500 r/min，进给量0.06 mm。

4.2 复合加工验证

采用最优参数进行验证试验,试件为人体下颌骨部分结构。如图8所示为3D打印及铣削复合加工后的结果，试件质量明显提高。

试件的3D打印时间、打印材料消耗量、储能模量分别为453 s、1 003.33 cm3、1 766.65 MPa，预测值分别为429.309 s、938.305 cm3、1 859.84 MPa，预测值与实际测量值相差分别为5.59%、6.93%、5.01%。铣削后试件的粗糙度为1.323 μm，与预测值1.247 μm相差6.1%。3D打印与铣削分别成功地验证了本研究所建立的模型。

5 结语

本文以3D打印与铣削的复合加工方式对PEEK材料人工骨进行加工研究，采用响应面法对3D打印工艺参数及铣削工艺参数进行了优化。经过对各响应值的显著性分析可知，文中所选取因素对应的各响应值影响均为极显著。经过回归拟合，得到各响应值对相应因素的回归方程。针对各回归模型对所选取因素进行优化，得出3D打印最优参数组合为层厚0.43 mm，内部填充密度55.05%，外周轮廓1.39圈；铣削工艺参数的最优组合为背吃刀量0.2 mm，主轴转速3 500 r/min，进给量0.06 mm。并进行了验证试验，成功验证了所构建模型及优化结果。

[1] 高丽花.温度波动下骨骼创伤修复中的聚醚醚酮(PEEK)仿生人工骨3D打印技术[J].科技通报,2017,33(2):125-128.

[2] 张钰.聚醚醚酮仿生人工骨3D打印热力学仿真及试验研究[D].长春：吉林大学,2014.

[3] 王镓垠,柴磊,刘利彪,等.人体器官3D打印的最新进展[J].机械工程学报,2014,50(23):119-127.

[4] 夏琰.组织工程化纳米-羟基磷灰石/聚己内酯人工骨支架的制备及其相关性能的研究[D].上海：第二军医大学,2013.

[5] 张永强.熔融沉积制备PHA/β-TCP三维多孔人工骨支架及其生物安全性评价[D].广州：南方医科大学,2017.

[6] 赵帝.仿生人工骨3D打印流场仿真分析及试件力学性能研究[D].长春：吉林大学,2015.

[7] 刘肖肖,吕福顺,刘原勇,等.一种增材与减材复合制造机研究[J].制造技术与机床,2017(6):49-52.

[8] 魏德强,李新凯,王优.基于响应面法碳素钢电子束表面微熔抛光研究[J].制造技术与机床,2017(3):89-93.

[9] 郭超,侯伟峰,范云鹏,等.响应面法优化丁香提取物的制备工艺[J].黑龙江畜牧兽医,2017(4):146-148.

[10] 胡建军,陈进,权凌霄,等.基于响应面法的液压集成块直角转弯流道优化[J].制造技术与机床,2017(9):78-83.

[11] Mohamed O A, Masood S H, Bhowmik J L.Mathematical modeling and FDM process parameters optimization using response surface methodology based on Q-optimal design [J].Applied Mathematical Modelling,2016,40(23-24):10052-10073.

[12] 吕福顺,刘肖肖,程祥,等.基于FDM的3D打印参数优化实验研究[J].组合机床与自动化加工技术,2017(9):114-117.