刀具姿态误差的优化研究*

吴志清 唐清春

(①广州工程技术职业学院, 广东 广州 510075; ②广西科技大学工程训练中心, 广西 柳州 545006)

五轴机床相比于三轴机床增加了两个回转轴，加工范围更为灵活，自由度更高,对于自由曲面高精度的加工有显著的效果[1],广泛运用于航空、航天的叶片类工件的精密加工。但是，由于增加两个回转轴使得机床的运动链更加复杂，产生了相应的原理性误差[2-3]。最典型的就是非线性误差。非线性误差产生原因是由于数控系统采用线性插补方式实现,导致在插补过程中刀轴矢量与回转轴间存在非线性关系，从而不能保证加工中刀具轨迹始终按照程序设计的路径运动，导致刀具姿态误差的产生，最终引起非线性误差。

解决刀具姿态误差，目前主要有两种方法：一是在前置处理中解决，二是通过后置处理中解决。对于方法一，目前研究有：毕庆贞等[4]提出了基于GPU的刀具可达性检测方法，在刀具的可行空间中进行刀轴可行性分析及刀具可达方向锥的计算；HO等[5]用等弧长逼近法先生成加工轨迹，然后通过控制调整加工轨迹以避免干涉；WANG等[6]提出了通过构造可行域的方法，控制刀轴矢量平滑过渡。对于方法二： TAKEUCHI等[8-9]提出在前置文件基础上对刀位点进行线性加密，通过限制最大线性误差值，插入中间点，缩小非线性误差；唐清春等[10]提出在前置文件基础上采用线性插补方法，并开发了专用后置处理软件运用到实际工程。因此，解决刀具姿态误差目前主要还是采用线性插补法，线性插补在一定程度上可以解决非线性误差问题，特别是曲率半径大，曲率变化小的自由曲面有良好的效果；但是对于曲率变化大，曲率半径小的自由曲面，就具有很大的局限性。因此有效控制非线性误差的大小具有十分重要的研究意义。

本文提出一种新的处理方式，从刀具姿态的角度来解决非线性误差。首先，从通用软件前置处理获得的刀位源文件，根据误差限制条件进行线性插补获得初始刀轴矢量；然后把获得的原始刀轴矢量进行投射获得新的刀轴矢量，投射的平面为插补前原始相邻刀轴矢量构成的平面；最后把新的刀轴矢量根据运动学模型转化为机床的控制角。通过国产双摆头五轴机床(AC式)仿真实验以及实际切削实验验证了该方法的正确性。

1 刀具姿态误差原理及优化

1.1 回转轴的线性插补运动

根据AC式双摆头机床运动结构，推导出在工件坐标系下旋转轴角度与刀轴矢量对应变换关系为：

(1)

设刀具相邻两点刀轴矢量分别为Ts(txs,tys,tzs)、Te(txe,tye,tze)，那么刀具在该处的角度分别为(As,Cs),(Ae,Ce)，假设在两刀轴矢量之间插入n个值，则有：

(2)

(3)

式中：下标i为当前点序号，i=0,1,…,n。

根据公式(1)可以得到，刀具在任意插补位置i的刀轴矢量为Ti(txi,tyi,tzi)为：

(4)

1.2 旋转角误差分析

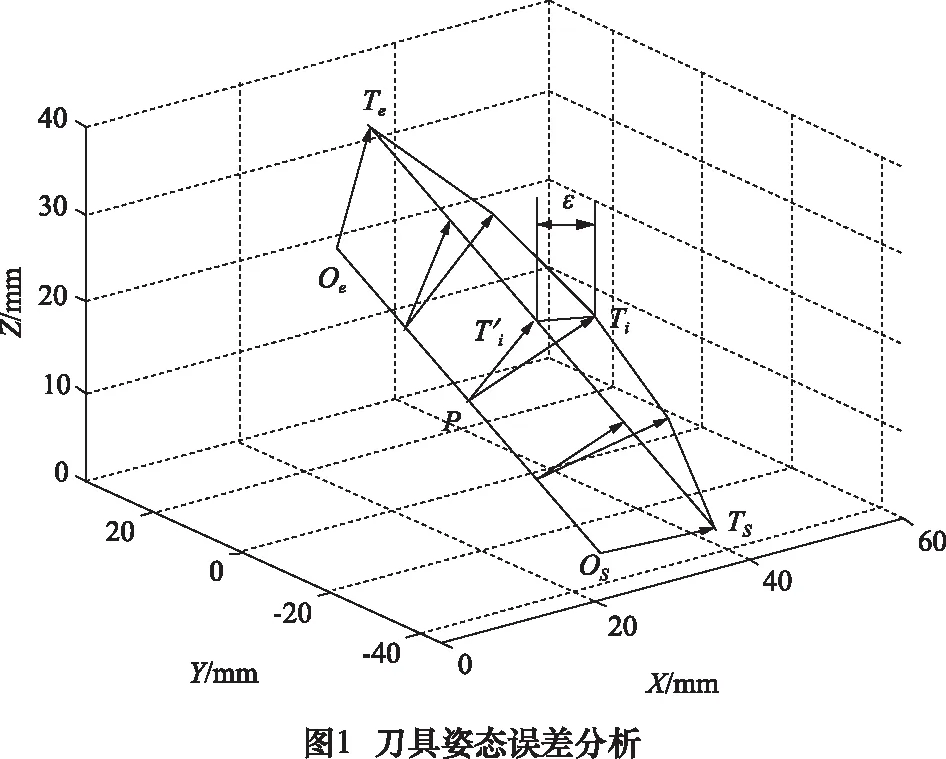
在线性插补过程中，刀具回转角产生的姿态误差可以由图1来直观表示。假设图中Os、Ts和Oe、Te分别为起点和终点坐标处的刀位点坐标、刀轴矢量，其中Os跟Oe连线为一直线，实际上是刀具的线性插补路径；Ts跟Te的连线有两条，直线为理论的刀轴矢量插补路线，曲线为实际的刀轴矢量插补路线，两者在中间位置产生最大误差为ε。

1.3 刀轴矢量投射方法

本文提出的刀轴矢量优化方法，具体实施为：将线性插补后的刀轴矢量投射到理论上始末两点矢量构成的平面上获得新的插补矢量，将获得的新的刀轴矢量再转换为机床的旋转角度，从而最终控制刀具在运动过程中按照线性插补的轨迹运动。

‖Ti-Ti′‖=εi

(5)

根据矢量内积原则有：

(Te-Ts)·(Ti-Ts)=‖Te-Ts‖×‖Ti′-Ts‖

(6)

(7)

根据公式(7)可以得出投射矢量Ti′为：

(8)

设Ti′为Ti′(txi′，tyi′，tzi′)，则根据公式(7)及公式(4)可得投射后的刀轴矢量：

(9)

公式(9)可简化为：

(10)

2 矢量投射插补与线性插补非线性误差仿真分析

本文利用MATLAB，任取两程序段的刀位源代码：

r1(251.958 2,-24.001 4,11.467 6,0.327 437,-0.463 40, 0.823 43),r2(251.956 4,-25.991 2,10.984 5,0.322 986,-0.480 14,0.815 56)。

与之对应的机床运动坐标分别为：M1(350.189 5,-26.540,-18.315 8,29.369 7,19.113 3),M2(348.852,-27.970 7,-19.799,30.486 3,18.843 6)。

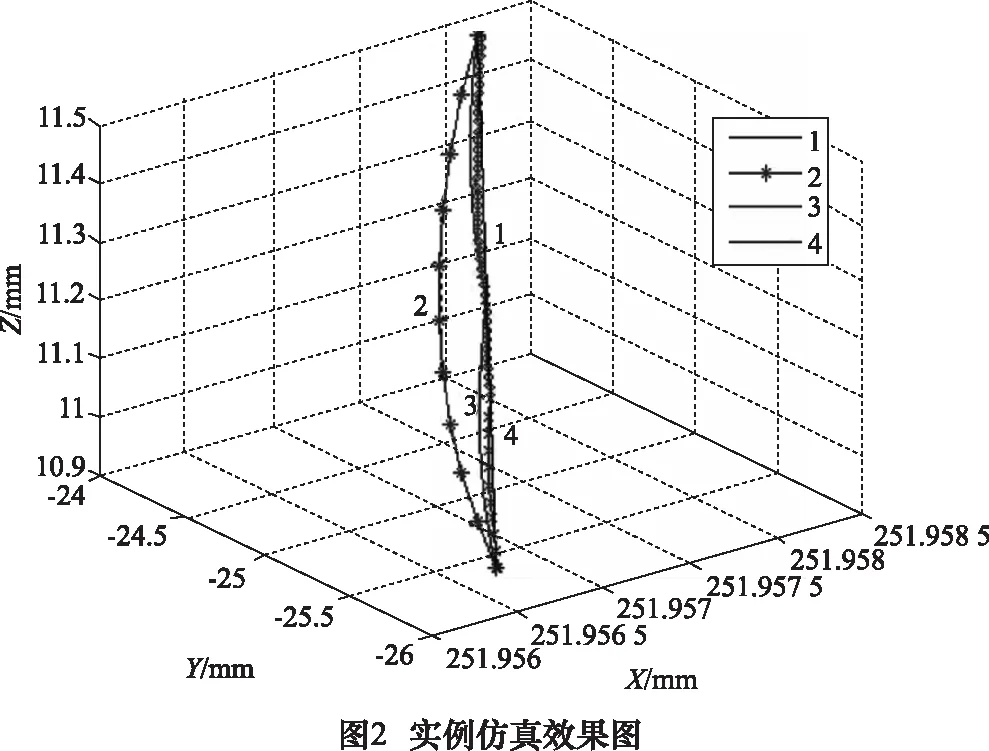
设摆长L为300 mm，进给速度为4 000 mm/min，进给周期为6 ms，根据上面算法，在MATLAB中的仿真结果如图2所示。

图2中分别采用四种情况来进行分析对比：曲线1表示理论编程直线，曲线2表示未补偿非线性误差的插补轨迹，曲线3表示采用了线性法的插补轨迹，曲线4表示采用刀轴矢量投射插补的插补轨迹。由仿真图可以看出，当采用刀轴矢量投射插补算法以及线性插补算法时，非线性误差大小得到显著减小，从效果上看，刀轴矢量投射算法插补轨迹比线性法插补误差更小。

3 叶轮加工及检测验证

通过仿真无碰撞和干涉后，在双摆头五轴机床上进行了叶轮的切削加工。为了对比效果，以两种插补方法进行加工，采用相同的转速、进给速度、残留高度及行距等工艺参数，只是在非线性误差处理时分别采用了线性插补和刀轴矢量投射插补方法，非线性误差判断值为0.02 mm。实验切削加工如图3所示。两种加工方法下的叶轮流道如图4。从图4可以看出，采用刀轴矢量投射插补方法后，流道刀路轨迹更加流畅，曲面的表面粗糙度也较好。

为了进一步直观比较两种加工方法，分别取两种加工状态下的叶片一截面通过三坐标采点实测，然后拟合为曲线与理论轮廓曲线比对，采用线性插补方法后，实测轮廓与理论轮廓最大误差为0.08 mm，进气边有部分过切，最大过切量为0.03 mm; 采用矢量投射方法后，实测轮廓与理论轮廓最大误差为0.04 mm，进汽边有部分过切，最大过切量为0.01 mm。对比结果如图5所示。

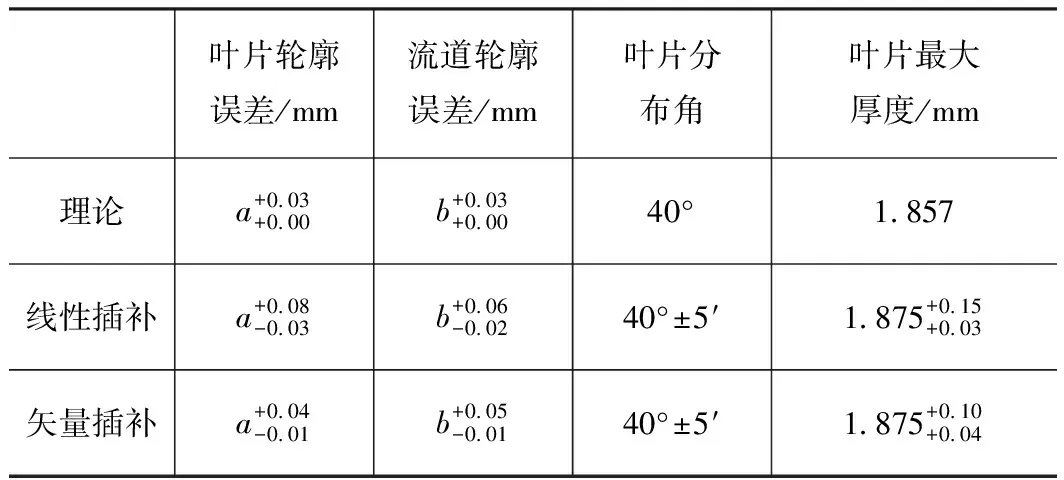
从图5看，采用刀轴矢量投射插补方法下的叶片比线性插补方法下的叶片光滑。通过三坐标实测同一截面对比可以看出，采用矢量投射方法后，实际加工的叶片轮廓与理论轮廓的轮廓误差由0.08 mm最大减小到0.04 mm，最大过切量也由0.03 mm减小到0.01 mm，说明采用矢量投射方法更能有效地控制刀具的姿态误差，避免刀具的剧烈摆动造成过切或者欠切现象。具体的测量数据如表1所示。

总的来说，在切削过程中，采用刀轴矢量投射插补算法后产生的NC代码在加工过程中在曲率变化较大的叶片进汽边以及流道未出现明显的过切、欠切现象，刀具在叶片翻边过程中，刀具未出现明显的颤动，过渡平稳，叶片内背弧曲面及过渡圆角处光滑，轮廓误差达到工艺设计要求，验证了该算法的正确性。最后完整的实物零件如图6所示。

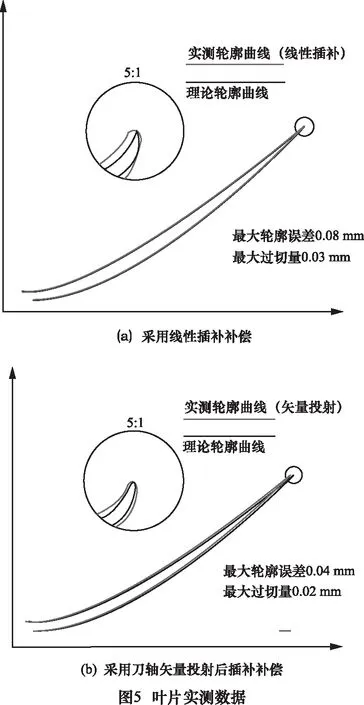
表1 两种方法切削测量数据比对

叶片轮廓误差/mm流道轮廓误差/mm叶片分布角叶片最大厚度/mm理论a+0.03+0.00b+0.03+0.0040°1.857线性插补a+0.08-0.03b+0.06-0.0240°±5′1.875+0.15+0.03矢量插补a+0.04-0.01b+0.05-0.0140°±5′1.875+0.10+0.04

4 结语

本文针对五轴机床在非线性插补过程中由于刀具姿态误差产生非线性误差问题，提出了一种矢量投射插补方法，基于后置处理技术有效提高了加工的轮廓精度。主要结论为：

(1)根据五轴联动原理，可分析出回转轴导致的刀具姿态误差模型并进行分析优化。

(2)基于相邻刀位点坐标及刀轴矢量，可建立矢量投射插补平面，通过设置误差判断条件值，可获得插补坐标值及矢量值。

(3)基于后置处理技术，利用机床的运动学模型，加载矢量投射插补算法，可有效提高零件的轮廓精度。

[1]周志雄，周秦源，任莹晖. 复杂曲面加工技术的研究现状与发展趋势[J]. 机械工程学报，2010，46(17)：105-113.

[2]吴大中，王宇晗，冯景春，等. 五坐标数控加工的非线性运动误差分析与控制[J].上海交通大学学报，2007，41(10)：1608-1612.

[3]杨旭静,周元生等.五轴数控加工中旋转轴运动引起的非线性误差分析及控制[J].机械工程学报，2012,48(3): 140-146.

[4]毕庆贞，王宇晗，朱利民，等.刀触点网格上整体光顺五轴数控加工刀轴方向的模型与算法[J].中国科学：技术科学，2010，40(10)：1159-1168.

[5] HO M C，HWANG Y R，HU C H. Five-axis tool orientation smoothing using quaternion interpolation algorithm [J]. International Journal of Machine Tool and Manufacture,2003,43(12):1259-1267.

[6] WANG Nan，TANG Kai. Automatic generation of gouge-free and angular-velocity-compliant five-axis toolpath[J]. Computer-Aided Design,2007,39(10):849-852.

[7]唐清春，陈其兵.叶片进出汽边刀路轨迹优化方法[J]. 汽轮机技术，2016(3)：238-240.

[8] Takeuchi Y，Shimizh H，Idemura T，et al. Five-axis controlled machining based on solid models[J].Journal of the Japan Society for Precision Engineering,1990,56(2)：111-116.

[9] CHO HD，JUN Y T，YANG M Y. Five-axis CNC millingfor effective machining of sculptured surfaces[J].International Journal of Production Research,1993,31(11):2559-2573.

[10]唐清春,范超.叶片五轴加工中非线性误差控制的研究[J].机床与液压，2014，42(2)：22-24.