APOS理论在导数概念教学中的应用

刘洪霞 周绍伟 郭花

【摘要】本文将APOS理论应用到导数概念的教学中，整节课通过活动、过程、对象、图式等阶段的逐层构建，使学生在原有知识的基础上建构新的数学知识，并通过问题驱动的教学方式，引导学生独立思考、合作探究，提高学生学习数学的积极性和主动性。

【关键词】APOS理论 问题驱动 导数的概念 教学设计

【中图分类号】G645 【文献标识码】A 【文章编号】2095-3089（2018）19-0005-02

一、引言

美国数学教育家杜宾斯基提出的APOS理论是对皮亚杰的“自反抽象”理论的拓展。APOS 理论认为数学概念的认知包含活动、过程、对象和图式四个阶段。该理论强调在学习数学概念时，要以实际生活中的问题为背景，老师精心设计教学活动，引导学生根据已有的知识经验，经过探究与归纳，建构新的知识。在教学中根据APOS理论进行教学设计，不仅有利于学生对数学概念的理解和掌握，还可以促使学生更加积极主动地学习。

杜宾斯基指出，活动、过程和对象是学生进行数学概念建构的三种状态，而图式就是将这三种状态与新概念有关的所有知识构成的认知结构或认知框架[1]。

我们经过多年的教学发现，学生普遍认为数学概念抽象难懂，学生对数学概念的掌握仅停留在被动记忆层面。而APOS理论可以有效地帮助学生了解数学概念产生的来龙去脉，从加深对数学概念的理解和掌握，基于APOS理论的概念学习框架图为：

二、基于APOS 理论的导数概念教学设计

导数的概念是高等数学中一元函数微分学的重要概念，也是整个高等数学中的重点内容。在学习导数概念前，学生已经学习了极限和连续的概念及简单的计算，初步具备一定的抽象思维能力。

1.活动阶段——设计问题情境，让学生形成直观的感性认识

在学习新概念时，教师通过实际问题引导学生逐步思考，在课堂教学中我们主要采用问题驱动的方式，学生通过分组协助积极参与到课堂教学中。

问题：在奥运比赛中，高台跳水是我国运动员的强项。请同学们思考：从数学的角度，我们该如何全面、准确地描述运动员的这样一个运动？

教师提示：运动员在空中的动作是非常复杂的，我们不考虑其动作，将运动员看作为一个质点，与这个質点的运动有关的是质点的位置、速度和时间，请同学们考虑如何找到位置、速度和时间的关系。

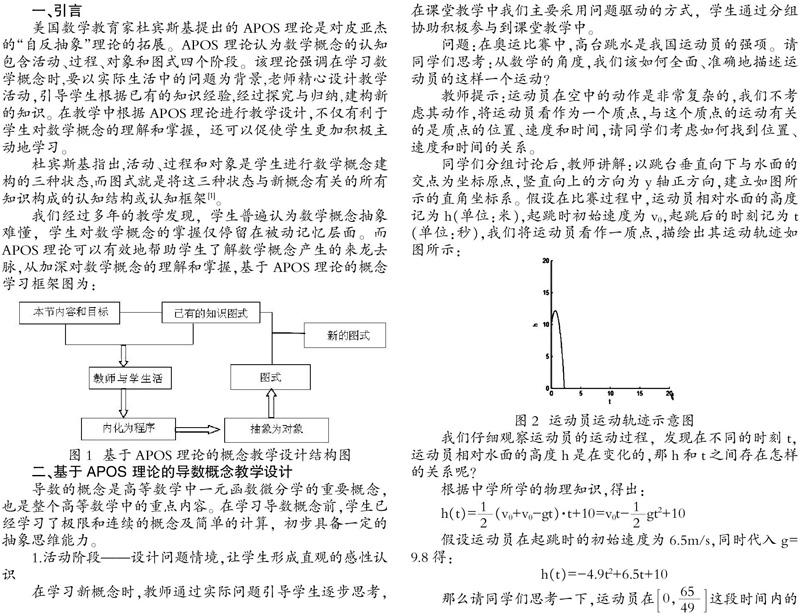
同学们分组讨论后，教师讲解：以跳台垂直向下与水面的交点为坐标原点，竖直向上的方向为y轴正方向，建立如图所示的直角坐标系。假设在比赛过程中，运动员相对水面的高度记为h（单位：米），起跳时初始速度为v0，起跳后的时刻记为t（单位：秒），我们将运动员看作一质点，描绘出其运动轨迹如图所示：

我们仔细观察运动员的运动过程，发现在不同的时刻t，运动员相对水面的高度h是在变化的，那h和t之间存在怎样的关系呢？

根据中学所学的物理知识，得出：

学生经过计算发现这段时间的平均速度为零，但是通过视频显示运动员一直在运动着，为什么计算结果是零呢？通过数值结果与现实矛盾的产生，我们意识到平均速度只能粗略地描述物体在某段时间的运动状态，无法刻画运动的细节，因为运动员的速度是时时刻刻改变的，平均速度不足以描述这个运动。

2.过程阶段 ——将活动阶段内化并抽象出概念

这就是瞬时速度这个概念的数学表示。其中△t是时间增量，而△t→0表示了这个增量逐步缩小的过程。

教师还可以用类似的思想引导学生解决股指“跳水”，房价“暴涨”，气温“陡增”，GDP“猛增”等变化率问题。

上述例子，虽然问题不同，但数学本质相同，都是函数值的变化和自变量变化的比值，即属于变化率问题。和学生一起总结出：

3.对象阶段 —— 通过探究和反思，形成导数的概念和几何意义

综合前面的思考过程，引导学生抛开问题的实际意义，抽象出导数的概念。那么如何判断函数在某一点是否可导呢？通过具体的例题让学生掌握导数概念的本质。进一步给出函数在某点不可导例题，从而引导学生给出导函数和单侧导数的概念。

通过问题探究引导学生思考导数的几何意义。

问题：中学学过圆的切线的定义，即与圆只有唯一交点的直线叫圆的切线，那么“与曲线有唯一交点的直线是该曲线的切线”这样定义曲线的切线合理吗？不合理的话如何给出曲线的切线的定义？此处，借助多媒体手段，形象地观察如何借助极限这个工具定义曲线的切线。

4.图式阶段 —— 整合活动、过程与对象阶段，形成清晰的图式结构

学生经过前面三个阶段的学习后，头脑中基本形成了概念的结构图，经过的长期、反复地学习，并与原有的图式进行整合，可以建立起综合的图式，从而能建立起知识点之间的前驱后继关系，对高等数学的知识体系有更深刻的理解。

我们仍采用问题驱动的教学方式。请同学们思考导数的概念可以解释生活中的哪些现象？设计这个问题的主要目的是让学生应用导数的概念解决实际问题，加深对所学知识的理解。最后请同学们思考导数与连续有什么区别与联系？可导是不是一定连续？连续是不是一定可导呢？

同学们讨论后总结出结论： 如果函数y=f（x）在点x0处可导，则它在点x0处一定连续。

那么定理的逆命题成立吗？即y=f（x）在点x0处连续，则它在点x0处可导吗？你能举出连续但不可导的函数吗？

通过上述问题的解答，让学生脑子里进一步形成导数概念的清晰的图示结构。

三、结束语

本节课我们首先通过跳台运员的速度等现象发现平均变化率对描述这些现象很有帮助，但是我们通过跳台运动员这样一个运动发现平均变化率只能描述事物变化的结果，但是不能描述事物变化的过程，因此我们看到引进瞬时变化率即导数的必要性。那是不是所有的函数都有导数呢？答案是否定的。不过有些函数虽然不可导，但从左侧或右侧看却是可导的，为此我们给出了单侧导数的概念。对照前面学习的连续，我们自然会思考连续和可导的关系。通过运用本节课的学习，我们体会到数学在日常生活中的应用，很多看似与数学无关的现象我们可以用数学方法来解释。请同学们以后多用数学的眼光看我们所处世界，你会发现数学因为应用而美丽。

参考文献：

[1]陈元祝，基于APOS 理论对概率概念教学方式的探究[D].西安：陕西师范大学，2015.

[2]王彩芬，曹荣荣，田磊等.基于APOS 理论的无穷级数概念认知分析[J].高等理科教育，2016，4：86-90.

[3]曾玉祥，APOS理论在高等数学概念探究式教学中的应用[J].教育探索，2013，5：42-43.

[4]钱丽娜，APOS 理论下的平均数概念教学研究[J].数学大世界，2017，25：47-48.

[5]李卫平，对信息化教学设计的探讨[J].高中数学教与学，2016，12：25-28.

[6]杨伟成，导数的概念教学设计[J].高中数学教与学，2012，7：32-34.

作者简介：

刘洪霞（1979-），山东科技大学讲师，女，硕士，主要从事数学教学与研究。