“化齐次构造二次函数法”在解一类不等式最值中的妙用*

●

(绍兴市第一中学,浙江 绍兴 312000)

在各地各类试卷中，以不等式或函数为背景的最值问题经常出现，不少学生对此类题型面露难色.以不等式或函数为背景的一般解法有：不等式法、三角换元、整体换元、判别式法等等，而化齐次法是一种通过构造等式或不等式，使得两边各项的次数相等，即齐次式，从而实现解题目标的一种数学转化策略.此法对二元齐次求最值问题有通性，我们一起来探索其中的乐趣.

1 代数背景下的化齐次法

例1设实数x，y满足4x2+y2-8=2xy，则4x2+y2的最小值为______.

(浙江省宁波市镇海中学2017年11月高三数学期中考试第14题)

分析1本题看似普通，4x2+y2在等式中已经出现，若能将2xy也用4x2+y2替换，则利用重要不等式即可解决.

由基本不等式可知

(1)

根据式(1)和已知式，可得

4x2+y2≤16，

发现求出了最大值并不是题目所需要的最小值.

可见不等号方向出现问题，那么问题究竟在哪里？

仔细观察已知式，我们发现，当4x2+y2取到最小值时，实数x，y必然一正一负，而式(1)中的不等式更适用于同号的x，y，因而放缩方向出现了问题.只需将式(1)改写成式(2)，

(2)

思考1本题看似普通实则暗藏玄机，若将4x2+y2改成求3x2+y2，似乎没这么凑巧了！而在实数x，y的大前提之下，贸然使用基本不等式也会出现不必要的问题.那么这类题是否存在通解呢？

分析2观察题干，易知题中给出的条件是一个二元二次方程，并且每项次数都为2，所求项次数也为2.

设t=4x2+y2≥0，则已知式可变形为

4x2+y2-2xy=8，

等号两边同时乘以t，得

(4x2+y2-2xy)·t=8·t=8(4x2+y2),

等号左右两边都是二元二次方程.当y=0时，方程有解，求得t=8；当y≠0时，变形得

(4t-32)x2-2txy+(t-8)y2=0，

即

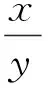
Δ=(2t)2-4(4t-32)(t-8)≥0，

得

思考2本题中的4x2+y2-8=2xy，4x2+y2=t其实为非标准方程的椭圆，标准方程的椭圆让很多学生望而生畏，更别说其他椭圆了.而“化齐次构造二次函数法”巧妙地避开了几何图形，转化为二次函数有解的问题，简单易懂，它适用于各项次数一样的式子.当然本题还可以采用二次整体换元法、三角换元法等.

笔者本以为例1中的各项次数都是2是凑巧，却在无意间发现此类题目早已出现在各自主招生考试中，也有同行通过拉格朗日乘数法、构造齐次分式等方法解决此类问题.但“化齐次构造二次函数法”更简单易懂.

变式1已知实数x，y，满足5x2-y2-4xy=5，则2x2+y2的最小值是______.

(2017年清华大学自主招生试题第12题)

解设t=2x2+y2≥0，在方程5x2-y2-4xy=5的两边同时乘以t，得

(5x2-y2-4xy)·t=5(2x2+y2)，

等号左右两边都是二元二次方程.当y=0时，方程有解，求得t=2；当y≠0时，变形得

(5t-10)x2-4txy-(t+5)y2=0，

即

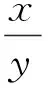
Δ=(4t)2+4(5t-10)(t+5)≥0，

得

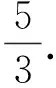
思考3从题目到解答，例1和变式1几乎一模一样.但对于变式1，不等式法显然无法直接配凑出来，体现了“化齐次构造二次函数法”在此类问题中的优越性，只需各项次数一样，其他没有任何要求.

变式2[1]若x2+2xy-y2=7(其中x,y∈R)，则x2+y2的最大值为______.

变式3若6x2+4y2+6xy=1，其中x,y∈R，则x2-y2的最大值为______.

(2017年浙江省宁波市数学高考模拟试题第17题)

笔者惊喜地发现此类题型受到了很多命题教师的青睐，抛开几何背景直接代数法求解，也成为了配齐次的一类题型.

2 几何背景下的化齐次法

例2[2]设P为曲线2x2-5xy+2y2=1上的动点，求点P到原点的距离最小值.

解设t=x2+y2≥0，在方程2x2-5xy+2y2=1的左右两边同时乘以t，得

(2x2-5xy+2y2)·t=1·(x2+y2)，

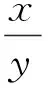
Δ=(5t)2-4(2t-1)2≥0，

得

3 解不等式最值中的工具：化齐次法

事实上，“化齐次构造二次函数法”要求各项次数一样，可以减弱成已知等式齐次，所求项齐次，方法仍然适用.

例3设x，y为实数，若4x2+xy+y2=1，则2x+y的最大值为______.

(2011年浙江省数学高考理科试题第16题)

分析本题短小精巧，可以从多个角度进行研究，解法较多，不等式法也比较简单．易知题中给出的条件是一个二元二次方程，并且每项次数都为2，问题中所求式2x+y每项次数都是1，能否用“化齐次构造二次函数法”呢？其实只要平方后即可实现问题和条件的齐次化形式．

解设t=(2x+y)2=4x2+4xy+y2≥0，在方程4x2+xy+y2=1的两边同时乘以t，得

(4x2+xy+y2)·t=1·(4x2+4xy+y2),

等号左右两边都是二元二次方程.当y=0时，方程有解，求得t=1；当y≠0时，变形得

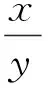
Δ=(t-4)2-4(4t-4)(t-1)≥0，

得

思考4本题直接用基本不等式更快捷，但这也不失为一种通法，齐次即可使用，关键也是配凑齐次.

(2016年金华十校高三数学调研试题第16题)

分析本题看似与“化齐次构造二次函数法”无关，实则紧密相连.若对于向量的模长采用代数法，则可得一个各项次数为2的不等式和一个各项次数为2的等式，符合适用范围，不妨尝试一下.

设向量a,b的夹角为θ，由|xa+yb|=1可知

x2+2xycosθ+y2=1(其中xy≥0).

(3)

不等式两边同时乘以等式(3)，可化成齐次不等式，即

15(x2+4xy+4y2)≤64·1=64(x2+2xycosθ+y2)

对xy≥0恒成立.当x=0时，方程有解，求得cosθ为任意值；当x≠0时，等号左右两边都是二元二次不等式，变形得

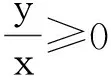
综上所述，以上高考试题、自主招生试题或模拟考试题，都是以不等式或函数为背景命制的最值问题.要顺利地解决此类问题，需要选择合适的解题途径，利用积累归纳迅速形成方法，而不是考试期间一一尝试.笔者给出“化齐次构造二次函数法”的通法，其优点在于通过对题目的“模式识别”，自助构建合理恰当的解题方法，加强了学生对数学转化思想的理解和认识，举一反三，会看题，看懂题，会做题，化同题.

参考文献

[1] 王耀．例谈“化齐次法”在解高考题中的应用[J]．数学通讯，2014(Z3)：52-54．

[2] 王芳,李光俊．关于拉格朗日乘数法的两点注记[J]．中学数学教学参考，2017(7):39-40．