基于自适应加权广义逆矢量方向滤波估计地震同相轴倾角
刘明忱,孙建国,韩复兴,孙章庆,孙 辉,刘志强
吉林大学地球探测科学与技术学院,长春 130026
0 引言
在地震数据处理和解释过程中,地震数据和地震图像的局部结构方向(倾角属性)提供了丰富的地层和地理信息,应用广泛。如:层析成像[1-3],偏移速度分析[2, 4],波场分离[5],数据去噪与导向滤波[6-7],Seislet变换[8],自动正常时差校正(ANMO)与成像[9-11],CRS(common reflection surface)叠加[12]等等。
对地震同相轴的方向估计有多种方法可以实现。1983年,Ottolini[13]提出了经典的倾斜叠加(线性Radon变换)方案来估计同相轴的方向,其基于相关或相似函数,利用叠加后能量值最大实现了同相轴局部斜率的提取;但这种方法效率不高,且估计值分辨率较低。Claerbout等[14]提出了平面波分解滤波器的概念,用于估计同相轴的方向和断层检测,借助多维预测误差滤波器的思想,根据地震数据的局部平面波模型,用有限差分模板解平面波微分方程来估计局部平面波;它能很好地应对地震数据中普遍存在的假频问题和斜率随空间和时间双变量变化的平面波,但该方法需要设置的参数很多,如滤波器类型、滤波器系数,滤波估计局部斑块的大小、数量和形状,迭代次数和正则化程度等,不容易控制和掌握。2002年,Fomel[15-16]完善了此概念,利用预测误差滤波器对同相轴方向进行估计,将所需参数降为一个具有明确物理意义的量,即局部平面波场的斜率参数,在计算的过程中不断迭代使残差达到最小值。另外,在实际资料处理中也采用瞬时倾角估计算法[17-18]。Barnes[19]和Fomel[20]采用不同方法对利用解析道估计的瞬时倾角进行光滑,在有限的横向分辨率损失下得到了更加稳定的瞬时倾角结果。
还可以采用有限差分方法估计同相轴方向。通过得到的梯度矢量求取倾角,计算速度快,容易实现;但是它本身是一阶导算子,并且趋向于放大高频噪声,需要对数据进行光滑来压制噪声和拾取大尺度特征。尽管有限差分方法很直接,但是它的结果却不能直接光滑。这是因为,波前有两个相反的法向方向,而方位是其中一个方向。例如,0°和180°倾角都是水平同相轴,但是它们的平均却是90°,是垂直的。因此,光滑并不能采用算数平均。方向和方位是两个概念。一个方向可以是一个单位矢量指向任何方向,而一个方位可以仅在一个指定的半矢量空间。解决矢量场的光滑问题,一种方式是采用结构张量[21]方法。结构张量具有反转不变性。它用矢量场与自身的外积构建张量场,通过低通滤波器在高斯邻域内光滑每个张量元素,然后对光滑窗中的张量场进行奇异值分解得到特征值和对应的特征向量。理想情况下,光滑窗中的矢量均指向同一方向,得到一个非零特征值和两个零特征值。非零特征值对应的特征向量即为局部结构的梯度方向。但是在实际条件下,由于噪声等干扰导致特征值均不为零,通常选取最大的特征值对应的特征向量方向作为梯度方向。但结构张量法也有局限性,即当主值不存在时,另外两个特征值较大,可能意味着附近存在断层等不一致的结构或者信噪比很低等情况。由于特征向量都是正交的,由此可能根据一个错误选取的特征值对应的特征向量进行光滑,也就得到了错误的倾角估计值。即使将错误选取的特征向量通过中值滤波等方法去除,也会导致额外的计算量和降低分辨率。
为了在断层等不连续位置处准确地估计倾角,并得到连续稳定的倾角估计剖面,本文提出自适应加权广义逆矢量方向滤波(weighted generalized inverse vector directional filters,WGIVDF)方法,并通过理论模型和实际数据的测试,验证本方法的有效性。
1 方法原理
1.1 改进的梯度算子
对于地震勘探来说,研究的空间通常为面向地下的下半空间。因此,假设水平面是由x和y坐标轴组成的平面,那么z轴垂直于水平面指向下半空间。首先,设定z轴的正方向为参考方向;然后,利用改进的梯度算子计算梯度矢量场,选出与参考方向角度差大于π/2的矢量,对矢量的各个分量乘以-1进行反转[22-23];最后,对矢量场应用自适应加权广义逆矢量方向滤波,得到稳定的倾角估计剖面。
计算地震数据的梯度矢量需要用到梯度算子。通常使用简单的有限差分进行计算。梯度算子在x和y方向的矩阵表示式为
(1)
(2)
其他常用的梯度算子包括Sobel算子、Prewitt算子等等。通过观察常用梯度算子的基本形态,可以得到关于梯度算子基于可控参数a的一般表达式:
(3)
(4)
调节可控参数a的值,能得到不同的梯度算子表达式。基于计算单一平面波时方向和能量误差最小的原则,可以确定a值的最优解。
在二维情况下,通过计算证明,当a=0.25时,得到的梯度算子可以使误差达到最小,即是改进的梯度算子[24]。在三维情况下,对于地震数据u,x方向的梯度vx可以表示为
a(ui+1,j+1,k+ui+1,j-1,k+ui+1,j,k+1+ui+1,j,k-1)-
a(ui-1,j+1,k+ui-1,j-1,k+ui-1,j,k+1+ui-1,j,k-1)+
b(ui+1,j+1,k+1+ui+1,j+1,k-1+ui+1,j-1,k+1+ui+1,j-1,k-1)-
b(ui-1,j+1,k+1+ui-1,j+1,k-1+ui-1,j-1,k+1+ui-1,j-1,k-1)]。
(5)
y、z方向的梯度vy和vz与vx表达式类似,这里不再列出。应用同样的方法可以得到三维情况下的最优梯度算子表达式,其中a=0.245,b=0.085。


图1 逆矢量示意图Fig.1 Inverse vector diagram
1.2 自适应加权广义逆矢量方向滤波
在图像处理领域中,矢量滤波应用非常广泛。常用的方法有矢量中值滤波器(VMF)、基本矢量方向滤波器(BVDF)和距离方向滤波器(DDF)等。这3种滤波器都是先计算滤波器窗口中每一点到其他所有计算点的聚合距离,然后使聚合距离最小化的值作为滤波器的输出。其中基本矢量方向滤波器基于角度聚合距离,是关于输入矢量方向的最大可能性估计,对输入矢量场的方向信息特别敏感,很适合作为反转矢量场的光滑滤波器。但是,当数据含有较大的噪声或者由复杂的地质结构产生时,在分析窗中计算的矢量准确性也会受到影响。矢量场经过聚合距离计算后,仅有一个矢量作为BVDF的输出,这时很可能是受到污染的结果输出,且有可能导致整体输出结果的不连续。对于这种情况,输出一组矢量替换此单独一个矢量,进行加权处理作为最后的结果。加权的广义逆矢量方向滤波器(WGIVDF)既能根据角度聚合距离来筛选矢量,又能对筛选出来的矢量进行加权处理。将滤波器窗口大小为W的矢量元素,按照从左到右、从上至下的顺序排列,写成{fi,i=1,2,…,n}∈W。两个矢量fi,fj的夹角距离A(fi,fj)为
(6)

(7)
窗口内所有样点计算的角度聚合距离αi按由小到大的顺序排列可以表示为
(8)
分别对应样点矢量
(9)


(10)
(11)

某一方向为中心的一组矢量束。这一过程剔除了远离中心的矢量,减少了在倾角估计中的不确定性。对选出的矢量束进行加权求和,进一步压制噪声并找到最中心的方向作为最后的WGIVDF输出:
(12)

(13)
式中:参数ω控制权函数的衰减零点;参数n控制权函数的衰减速率。
图2给出了权函数的参数响应曲线。当ω=0.5时(图2a),n值越大,权函数的衰减速率越快;当n=2时(图2b),ω值越大,权函数的衰减零点越靠近0值。由三角函数的性质可知:当n为偶数时,余弦函数cosnx的函数周期为T=π;当n为奇数时,周期为T=2π。为了保证权函数的值落在[0, 1],通常选取n为偶数。进一步由参数ω确定余弦函数的周期为T=π/ω,也就决定了函数零点的位置π/(2ω)。利用权函数的参数性质,根据需要合理确定ω和n的值。在本文中,选取ω=0.5和n=2作为权函数的参数取值。

图2 权函数参数响应Fig.2 Weighting function parameter response
WGIVDF利用角度聚合距离将滤波窗内方向最为接近的矢量选取出来。根据权函数,将角度聚合距离最小的也就是最靠近中心的矢量给予最大的权,而其他矢量赋予较小的权,使输出矢量变为指向最中心的矢量。而对于由于噪声或断层的影响造成矢量失准的情况,在加权平均的过程中,失准矢量的不准确部分相互抵消,从而最大限度地保证了矢量的准确性。根据最终输出的矢量,即可得到当前位置处的斜率p和矢量与水平轴的夹角。
1.3 计算策略
在二维地震数据处理中,计算量问题并不需要太多关注,而在三维数据处理中计算同相轴倾角属性,就需要考虑计算量的问题。在本方法中,需要计算滤波窗口中所有矢量之间的角度聚合距离,通过移动滤波窗口遍历数据体来完成全部的计算。对于大小为Nx×Ny×Nz的滤波窗口,需要计算的数据量为
(14)
但是,在实际计算中可以发现,在滤波窗口重叠的部分有大量的矢量角度聚合距离被重复计算。本文给出一种计算矢量角度聚合距离的方案,可以将计算量降低一个量级。如图3所示,当前滤波窗口中的待计算矢量由白色和黑色点组成。当滤波窗口向y轴方向移动一个单位时,与上一滤波窗口重复的矢量由黑色点表示,共有NxNz(Ny-1)个,而仅有NxNz个新的待计算矢量,即图中灰色点位置。此时,只需要计算重复的矢量与新矢量和新矢量相互之间的角度聚合距离,即可达到之前的计算目的,从而节省了计算成本,加快计算速度。这样,采用这种方案后的计算量为
(15)
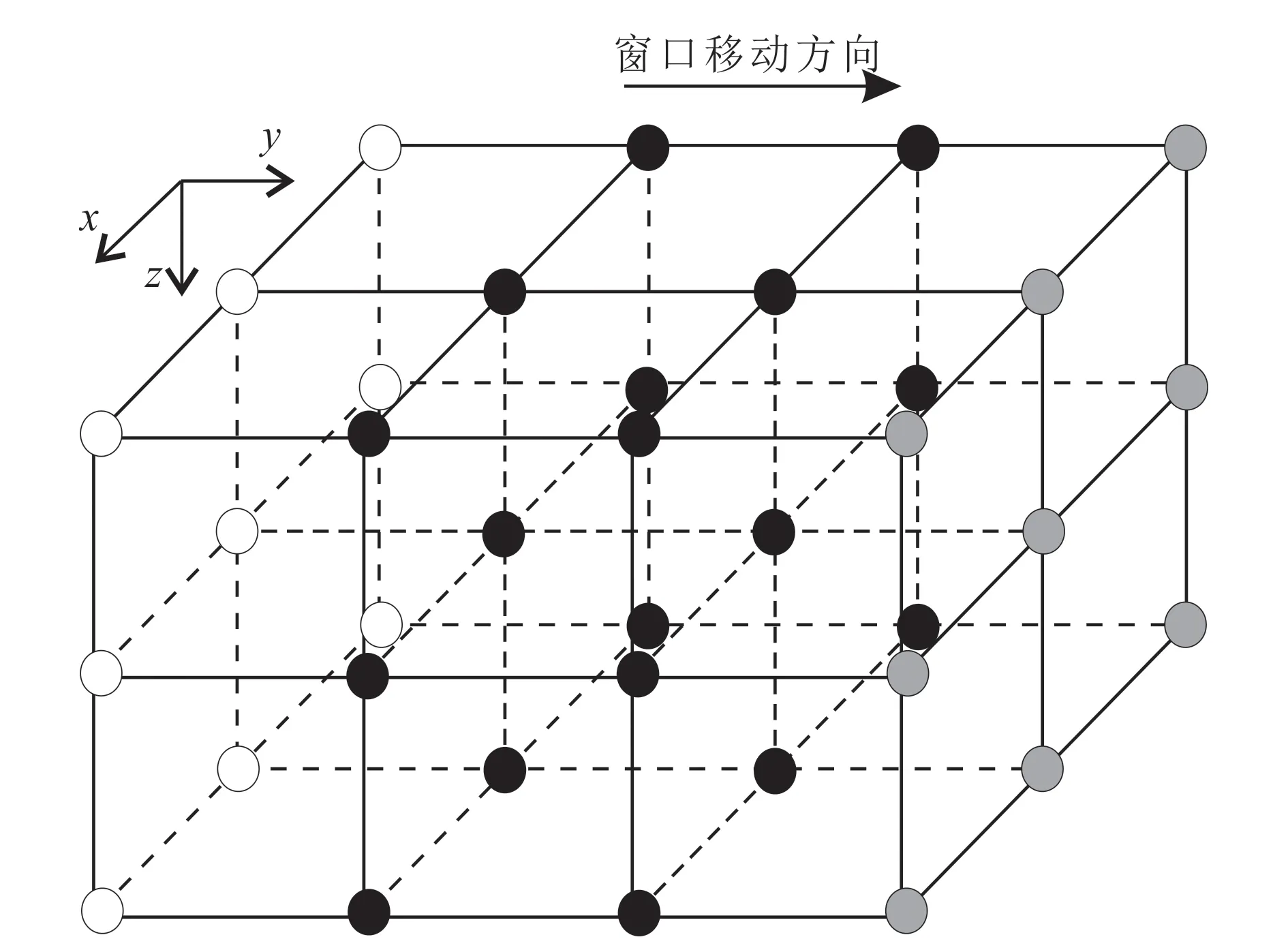
白点和黑点组成了当前滤波窗内的待计算矢量,灰点和黑点组成了下一滤波窗内的待计算矢量;黑点表示两滤波窗相互重合的部分。图3 滤波窗口移动示意图Fig.3 Direction of filter window moving
2 数值算例
为了验证本方法,选取了两个理论模型进行测试,规定向右倾的倾角为正,向左倾的倾角为负。第一个模型(图4a)为包含不同倾角地层与多种不整合接触类型的简单模型,由三部分组成:左边部分是倾角为15°的倾斜层;中间部分是倾角为0°的水平层;右侧部分是倾角为30°的倾斜层,倾向与左侧15°倾斜层相反。三层的相互接触部分被断层所分隔,形成了3个不同的断层接触面。由改进的梯度算子计算出的梯度矢量场,经过逆矢量计算后的矢量分布如图4a所示。应用WGIVDF,采用3×3的滤波窗口,权函数参数ω=0.5、n=2去光滑逆矢量场,得到如图4b所示的结果。为了与本文的WGIVDF倾角估计方法进行对比,选取平面波解构滤波器方法和结构张量方法来估计模型倾角,其结果分别如图4c和图4d所示。平面波解构滤波器方法在计算过程中没有使用光滑窗。从图4中可以看出,3种方法在平坦区域的倾角估计稳定,准确地反映了平坦区域的倾角。但在断层区域针对不同类型的断层:WGIVDF方法在边缘处倾角估计稳健,具有最高的分辨率;平面波解构滤波器方法在边缘处的表现介于WGIVDF方法和结构张量方法之间;结构张量方法在边缘处的表现最差,产生了很多 “锯齿状”的不稳定性估计。这主要是由于结构张量方法在高斯邻域内的平均效应引起的。WGIVDF方法能够有效和高分辨率地估计地层与断层处的倾角,有较强的倾角信号细节估计能力。

a.理论模型与相应的逆矢量;b.WGIVDF;c.平面波解构滤波器;d.结构张量。图4 不同倾角估计方法在理论模型上的倾角估计结果Fig.4 Dip estimation results of different dip estimation methods on theoretical model

a.sigmoid模型;b.WGIVDF;c.平面波解构滤波器;d.结构张量。图5 不同倾角估计方法在sigmoid模型上的倾角估计结果Fig.5 Dip estimation results of different dip estimation methods on sigmoid model
第二个模型(sigmoid模型,图5a)为理论合成地震记录[25],包含顶部的多个倾斜地层、一个断层界面、一个不整合接触面、向斜和背斜地层结构。图5b为应用WGIVDF方法计算的局部地震倾角剖面。图5c和图5d分别为应用平面波解构滤波器方法和结构张量方法估计的局部地震倾角剖面。对比图5b、c、d中的局部地震倾角估计结果:WGIVDF方法对平坦区域的倾角估计准确,对断层和不整合部分的边缘显示清晰,分辨率高,细节保护能力强。平面波解构滤波器方法和结构张量方法在平坦区域倾角估计的过程中表现是比较稳定的;平面波解构滤波器方法采用了3×3的光滑窗口,得到的局部地震倾角剖面变化平缓,边缘也较为清晰,效果介于另外两种方法之间;而结构张量方法在断层和不整合区域附近的估计值平均效应明显,分辨率较低。
从上述分析比较可以看出:在不同模型下,相比于平面波解构滤波器方法和结构张量方法,本文的WGIVDF方法对断层和不连续等边缘处的倾角估计准确,分辨率高,受断层等不连续结构影响小,估计的局部地震倾角剖面稳定,变化连续;结构张量方法在高斯邻域内的光滑作用明显,使得局部地震倾角剖面光滑均匀的变化,但也掩盖了许多边缘细节信息;平面波解构滤波器方法的作用则介于两者之间。这里需要注意的地方是:1)光滑窗口对于3种方法来说概念并不相同。对于WGIVDF方法是一种矢量光滑窗口,而对于平面波解构滤波器方法和结构张量方法来说,则是标量光滑窗,是一种局部的标量平均。WGIVDF方法在矢量光滑后依然可以进行标量光滑,用以压制不合逻辑的突变点。这样既保持了WGIVDF方法刻画局部地震倾角的高分辨率,又能在需要时得到更加稳定的倾角剖面。2)平面波解构滤波器方法在计算过程中需要进行迭代逼近,相比于另外两种方法更为耗时。
3 实际数据
基于理论分析结果,进一步将WGIVDF方法应用于实际地震资料中。选取墨西哥湾某地区的时间偏移剖面[25](图6a)对本文的方法进行测试。偏移剖面层状结构中包含多个断层和不同的起伏结构。分别应用WGIVDF、平面波解构滤波器和结构张量方法估计局部地震倾角剖面,其结果显示如图6b—d所示。这里,局部地震倾角剖面转换为用同相轴斜率p来表示。WGIVDF采用了3×3的滤波窗口和与之前相同的权函数参数ω=0.5、n=2(如图2a中的实线)去估计倾角剖面。平面波解构滤波器方法依然沿用了3×3的光滑窗口。从图6b—d中可以看出:结构张量方法的光滑平均损失了大量的细节结构信息,上面主要的断层结构也被模糊,失真现象明显;WGIVDF和平面波解构滤波器方法估计的局部地震倾角结果相差不多,但WGIVDF细节信息更多,分辨率更高。
4 结论
1)本文提出一种基于自适应加权广义逆矢量方向滤波(WGIVDF)来估计地震资料的局部地震倾角剖面的方法。
2)本方法使用一种改进的梯度算子计算得到地震数据的梯度矢量场,采用逆矢量方法将得到的梯度矢量场统一指向下半空间,根据在矢量光滑窗中矢量间的角度聚合距离确定自适应权系数,从梯度矢量场中计算矢量光滑窗中相似度最高、最中心的自适应加权矢量作为估计倾角的矢量,得到的局部地震倾角剖面具有分辨率高、稳健性强、边缘清晰、细节保护好等特点。
3)不同于平面波解构滤波器和结构张量等方法,WGIVDF是一种矢量滤波方法,在计算效率上与结构张量算法相当,优于平面波分解滤波器算法。通过对比不同方法在理论模型和实际数据的处理结果分析,WGIVDF方法在平坦区域能够稳健估计地震资料的倾角。在断层等不连续区域的边缘,与平面波解构滤波器和结构张量方法相比,估计的倾角具有较高的分辨率,很好地保护了细节信息。
(
):
[1] Billette F, Lambaré G. Velocity Macro-Model Estima-tion from Seismic Reflection Data by Stereotomography[J].Geophysical Journal International, 1998, 135(2): 671-690.
[2] Lambaré G. Stereotomography[J]. Geophysics, 2008, 73(5): VE25-VE34.
[3] 王宇翔, 杨锴, 杨小椿, 等. 基于梯度平方结构张量算法的高密度二维立体层析反演[J]. 地球物理学报, 2016, 59(1): 263-276.
Wang Yuxiang, Yang Kai, Yang Xiaochun, et al. A High-Density Stereo-Tomography Method Based on the Gradient Square Structure Tensors Algorithm[J].Chinese Journal of Geophysics, 2016, 59(1): 263-276.
[4] 李振伟, 杨锴, 倪瑶, 等. 基于立体层析反演的偏移速度建模应用研究[J].石油物探, 2014, 53(4): 444-452.
Li Zhenwei, Yang Kai, Ni Yao, et al. Migration Velocity Analysis with Stereo-Tomography Inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 444-452.
[5] 杜婧, 王尚旭, 刘国昌, 等. 基于局部斜率属性的VSP波场分离研究[J]. 地球物理学报, 2009, 52(7): 1867-1872.
Du Jing, Wang Shangxu, Liu Guochang, et al. VSP Wavefield Separation Using Local Slopes Attribute[J].Chinese Journal of Geophysics, 2009, 52(7): 1867-1872.
[6] 刘洋, 王典, 刘财, 等. 局部相关加权中值滤波技术及其在叠后随机噪声衰减中的应用[J]. 地球物理学报, 2011, 54(2): 358-367.
Liu Yang, Wang Dian, Liu Cai, et al. Weighted Median Filter Based on Local Correlation and Its Application to Poststack Random Noise Attenuation[J]. Chinese Journal of Geophysics, 2011, 54(2): 358-367.
[7] 刘洋, 王典, 刘财, 等. 基于非平稳相似性系数的构造导向滤波及断层检测方法[J]. 地球物理学报, 2014, 57(4): 1177-1187.
Liu Yang, Wang Dian, Liu Cai, et al. Structure-Oriented Filtering and Fault Detection Based on Nonstationary Similarity[J]. Chinese Journal of Geophysics, 2014, 57(4): 1177-1187.
[8] Fomel S, Liu Y. Seislet Transform and Seislet Frame[J]. Geophysics, 2010, 75(3): V25-V38.
[9] Fomel S. Velocity-Independent Time-Domain Seismic Imaging Using Local Event Slopes[J].Geophysics, 2007, 72(3): S139-S147.
[10]Cooke D, Bóna A, Hansen B. Simultaneous Time Imaging, Velocity Estimation, and Multiple Suppression Using Local Event Slopes[J]. Geophysics, 2009, 74(6): WCA65-WCA73.
[11] 石秀林, 孙建国, 孙辉, 等. 基于波前构建法的时间域深度偏移:delta波包途径[J]. 吉林大学学报(地球科学版), 2016, 46(6): 1847-1854.
Shi Xiulin, Sun Jianguo, Sun Hui, et al. Depth Migration in Time Domain Using Wavefront Construction: Delta Packet Approach[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(6): 1847-1854.
[12]Hertweck T, Schleicher J, Mann J. Data Stacking Beyond CMP[J].The Leading Edge, 2007, 26(7): 818-827.
[13]Ottolini R. Velocity Independent Seismic Imaging[R]. Palo Alto: Stanford University, 1983: 59-68.
[14] Claerbout J F, Gubbins D. Earth Sounding Analysis: Processing Versus Inversion[J]. Nature, 1994, 370: 190.
[15]Fomel S. Applications of Plane-Wave Destruction Filters[J]. Geophysics, 2002, 67(6): 1946-1960.
[16] Fomel S. Shaping Regularization in Geophysical- Esti-mation Problems[J]. Geophysics, 2007, 72(2): R29-R36.
[17]Barnes A E. The Calculation of Instantaneous Fre-quency and Instantaneous Bandwidth[J]. Geophysics, 1992, 57(11):1520-1524.
[18] Barnes A E. Theory of 2-D Complex Seismic Trace Analysis[J]. Geophysics, 1996, 61(1): 264-272.
[19] Barnes A E. Weighted Average Seismic Attributes[J]. Geophysics, 2000, 65(1): 275-285.
[20] Fomel S. Local Seismic Attributes[J]. Geophysics, 2007, 72(3): A29-A33.
[21] Bakker P. Image Structure Analysis for Seismic Inter-pretation[D]. Delft: Delft University of Technology, 2002.
[22] Wang W, Gao J H, Chen W C. Robust Estimates of Seismic Reflector Orientations with Weighted Vector Directional Filter[J]. Journal of Seismic Exploration, 2011, 20(2): 119-134.
[23] Wang Y E, Luo Y, Alfaraj M. Inverse-Vector App-roach for Smoothing Dips and Azimuths[J]. Geophysics, 2008, 73(6): P9.
[24]Alfaraj M, Wang Y, Luo Y. Enhanced Isotropic Gradient Operator[J]. Geophysical Prospecting, 2014, 62(3): 507-517.
[25] Claerbout J F. Basic Earth Imaging: Stanford Explo-ration Project[DB/OL].[2017-02-20]. http://sepwww.stanford. edu/sep/prof/.

